《Gibbs Sampling for the UniniTiated》阅读笔记(上)---参数估计方法及Gibbs Sampling简介

《Gibbs Sampling for the UniniTiated》阅读笔记(上)---参数估计方法及Gibbs Sampling简介

前一阵子折腾的事儿太多，写了点东西都没有传上来，是我偷懒了- -，下不为例。

这篇文章基本上是来自于《Gibbs Sampling for the UniniTiated》，说是笔记其实和翻译也差不多了。

整个结构分为上中下三部分：

1.  参数估计方法及Gibbs Sampling简介
2. 一个朴素贝叶斯文档模型例子
3. 连续型参数求积分的思考

---

这篇是上部分，介绍基础参数估计和Gibbs Sampling概念。

为什么求积分—参数估计方法

很多概率模型的算法并不需要使用积分，只要对概率求和就行了（比如隐马尔科夫链的Baum-Welch算法），那么什么时候用到求积分呢？—— 当为了获得概率密度估计的时候，比如说根据一句话前面部分的文本估计下一个词的概率，根据email的内容估计它是否是垃圾邮件的概率等等。为了估计概率密度，一般有MLE（最大似然估计），MAP（最大后验估计），bayesian estimation（贝叶斯估计）三种方法。

最大似然估计

这里举一个例子来讲最大似然估计。假设我们有一个硬币，它扔出正面的概率 π 不确定，我们扔了10次，结果为HHHHTTTTTT（H为正面，T为反面）。利用最大似然估计的话，很容易得到下一次为正面的概率为0.4,因为它估计的是使观察数据产生的概率最大的参数。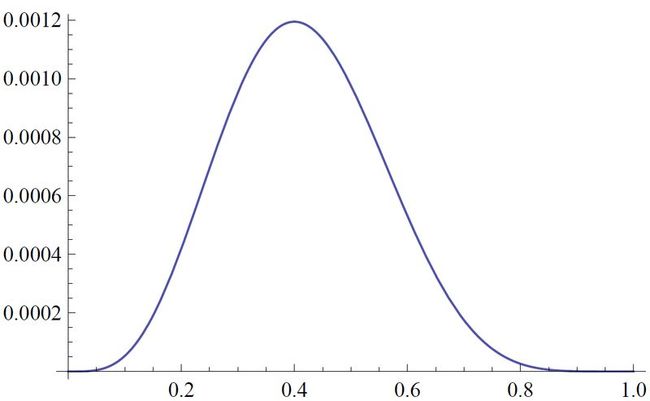first

令 χ={HHHHTTTTTT} 代表观察到的数据, y 为下一次抛硬币可能的结果,估计公式如下:

π~MLEP(y|χ)=argmaxπP(χ|π)≈∫πp(y|π~MLE)P(π|χ)dπ=p(y|π~MLE)(1)

### 最大后验估计

最大似然估计是直接最大化似然函数对参数进行估计。如果我们有一些关于硬币的先验知识的话（比如我们知道参数 π 服从某个形式的概率分布)，那么根据贝叶斯公式，我们就能求得观察到数据之后 π 的后验概率，令后验概率最大化

π~MAPP(y|χ)=argmaxπP(π|χ)=argmaxπP(χ|π)P(π)P(χ)=argmaxπP(χ|π)P(π)≈∫πp(y|π~MAP)P(π|χ)dπ=p(y|π~MAP)(2)

这里 P(χ) 与参数 π 无关就省略了。假设我们取一个令 P(π) 的期望为0.5的先验分布，那么之后观察到的数据将对之前假设硬币正反概率一样的bias 产生影响。

贝叶斯估计

首先我们可以看到,最大似然估计和最大后验估计都是基于一个假设，即把待估计的参数 π 看做是一个固定的值，只是其取值未知。而最大似然是最简单的形式，其假定参数虽然未知，但是是确定值，就是找到使得样本对数似然分布最大的参数。而最大后验，只是优化函数为后验概率形式，多了一个先验概率项。 而贝叶斯估计和二者最大的不同在于，它假定参数是一个随机的变量，不是确定值。在样本分布 P(π|χ)  上， π 是有可能取从0到1的任意一个值的，只是取到的概率不同。而MAP和MLE只取了整个概率分布 P(π|χ)  上的一个点，丢失了一些观察到的数据 χ 给予的信息（这也就是经典统计学派和贝叶斯学派最大的分歧所在。）

为了利用所有的信息，我们可以对参数的概率分布求期望值。对于一个离散型变量 z 的函数 f(z) 的期望一般是这样求得

E[f(z)]=∑z∈Zf(z)p(z)(3)

这里 Z 是所有 z 可能取的值， p(z) 是取这个值的概率。如果 z  是个连续型的变量，期望就是求积分而不是求和了:

E[f(z)]=∫f(z)p(z)dz(4)

对于这里的例子来说, z=π ,函数 f(z)=P(y|π) （这里文章讲的不清楚，这个 P(y|π) 是模型生成该结果的概率，而 P(π|χ) 是使用这个模型的概率，比如说有3个模型，第一个模型生成该数据的概率为0.5，第二个为0.4，第三个为0.3，需要考虑模型的结果），需要取期望的概率分布为 P(π|χ) ，所以整个期望是模型的所有分布上生成该数据的概率

P(y|χ)=∫P(y|π)P(π|χ)dπ(5)

对 P(π|χ) 我们使用贝叶斯公式

P(π|χ)=P(χ|π)P(π)P(χ)=P(χ|π)P(π)∫πP(χ|π)P(π)dπ(6)

要注意这里的后验概率是个函数，而不是像之前的MAP一样是个值，它充分考虑了 π 的先验知识和根据观察数据 χ 获得的信息，并将它们联系起来。

为什么抽样–Gibbs-Sampling

积分存在的一个问题就是他们很难算。事实上，之前的后验概率里面的分母很可能没有解析解，这个时候就要用抽样的方法获得这个概率分布的具体形式了。

Monte Carlo算法

Gibbs 抽样是Markov Chain Monte Carlo(蒙特卡洛方法）的一种。所谓的蒙特卡洛方法就是模拟统计的方法，举一个例子：假设有一个正方形和它的内接圆，然后我们随机地往正方形上撒很多很多的米粒，最后统计那些在圆里面的米粒数据（记作C），然后那些在正方形里的米粒数目（记作S)。可以看到两者之比近似于圆和正方形的面积之比：

CS≈π(d2)2d2(7)

这样我们就可以得到 π≈4CS ，这是一个典型的通过模拟来积分的例子，这里的圆面积是通过无数个点加和来逼近真实面积的。

在这个例子里，我们是对一个均匀分布采用来求值。回到刚才我们的问题，是要计算期望值 Ep(x)[f(x)] ，这里我们未知的是概率分布 p(x) ，假设它不是一个均匀分布，而且很难获得解析解。second图2给出了 f(z) 和 p(z) 的例子。从概念上来说，之前的积分应该是在 z 的所有空间上对 f(z)p(z) 加和所得到的结果。换一种角度来看，如果我们从 p(z) 随机依次抽取 N  个点 z(0),z(1),z(2),…,z(N) ,当 N 趋向于无穷的时候，我们可以通过无数个采样获得的点 z  来逼近它真实的概率分布，就有

Ep(x)[f(x)]=limN→∞1N∑t=1Nf(z(t))(8)

当 z 是离散变量的时候， f(z) 的期望就是加权平均，每个 z 的权值就是它的概率。当 z 是连续变量是，我们也可以用类似的想法，对于所有采样得到 z ，我们都用观察到的频率 1Ncount(z)(N→∞) 代替真实的概率 p(z) ，所以 p(z) 就隐含在采样得到的样本之中（这个想法是直观上的，因为实际上连续变量统计样本 z 出现的次数 count(z) 是没有意义的）。很容易可以发现，在整个 p(z)  的分布上，概率大的地方被采样的次数也多。

上面的式子 N 是趋向于无穷大的，我们也可以使用有限数目 T 的点来获得一个比较近似的值。

Ep(x)[f(x)]≈1T∑t=1Tf(z(t))(9)

好，现在我们有近似获得积分值的方法了。剩下的问题就是，如何根据 p(z) 采样出样本 z(0),z(1),z(2),…,z(T) 。这正好是模拟统计所研究的问题，所以有很多很多的采样方法，比如rejection sampling ,adaptive sampling, important sampling等等(见PRML），而我们采样的方法把 z  看做状态空间中的点，用从 z(0)  转移到 z(1)  再转移到 z(2)  这样的方式遍历 z  的状态空间，见图2。

可以看到 Z 的状态转移是一条马尔科夫链，这里 g 是一个根据转移概率 Ptrans(z(t+1)|z(0),z(1),…,z(t)) 来决定下一个状态是什么的函数。由Markov Chain 的性质，我们可以知道下一个状态 z(t+1)  仅仅取决于当前状态 z(t) 。

Ptrans(z(t+1)|z(0),z(1),…,z(t))=Ptrans(z(t+1)|z(t))(10)

而Markov Chain Monte Carlo方法的核心就在于如何设计这个函数 g 使得访问状态 z 的概率刚好是 p(z) ，这就需要转移概率 Ptrans 满足一定的条件（平稳细致条件，详见PRML的第四章)，而Gibbs sampling就是满足该条件的抽样方法之一。

Gibbs sampling算法

假设每个点  z=<z01,…,z0k>(k>1) 。Gibbs Sampling 每次在确定下一个状态的时候，并不是一次性地确定所有维度上的值，而是选取一个维度，通过剩下的 k−1 个维度来确定这个维度的值，见图2。

通过条件概率的定义我们可以得到

=P(Zi|z(t+1)1,…,z(t+1)i−1,z(t)i+1,…,ztk)P(z(t+1)1,…,z(t+1)i−1,z(t)i,z(t)i+1,…,z(t)k)P(z(t+1)1,…,z(t+1)i−1,z(t)i+1,…,z(t)k)(11)

注意右式的分子部分是全联合概率，而分母部分少了 z(t)i 这个维度，也就是我们要估计的这个维度。把这个操作对每个维度都采样一遍我们就得到了下一个新的点 z(t+1)=g(z(t))=<z(t+1)1,…,z(t+1)k> 。要注意的是每次新采样得到的值都可以直接用于下一次采样，所以公式里 z(t)i+1 前面的维度上标都是 t+1 ，因为他们都刚刚被采样过。

吐槽的部分

一般文章对Gibbs Sampling的介绍也就到此为止了，这样的介绍对新手来说（比如我- -)太难了,讲了也不会用。比如以下问题：

• 对特定的模型Gibbs Sampling条件概率的分布采样到底是咋做的？

• 连续型的参数变量如何处理？

• 只做 T 次循环怎么确保获得你想要的期望值？

于是这篇文章又生动活泼地举了一个从朴素贝叶斯模型生成Gibbs 采样器的例子。（见中篇）

参考文献：

1. 《Pattern Recognition and Machine Learning》

2. 《LDA数学八卦》

3. http://www.xperseverance.net/blogs/2013/03/1682/

4. 《Gibbs Sampling for the UniniTiated》