Gibbs Sampling for the Uninitiated
这几天较空总算把《Gibbs Sampling for the Uninitiated》看明白了点,看完这个对其他模型的 Gibbs Sampling 感觉应该是不会有大问题了,之后可以再仔细看看《Parameter estimation for text analysis》,然后对照他的代码写一份总结。
在此真是万分感谢这个作者,拯救了万千Uninitiated!要是没有这样的tutorial,也没人教,谁特么知道这东西怎么弄。
基础知识:随机过程、马尔科夫蒙特卡洛、Gibbs Sampling的理论基础(待写)
注:本文档主要是Learning Note,而不是独立教程,因此没有:1、基础概念 2、符号解释 3、详细公式推导 这些都可以从《Gibbs Sampling for the Uninitiated》原文找到。我的水平也极其有限,同时我认为如果只看别人博客而不愿意读原文那么肯定是不成的!本文主要目的是写一个学习记录给自己,使得以后忘记的时候能够迅速回顾。若能达到与人交流的目的,那就更好啦。
————————— 伟大的分割线:Gibbs Sampling for the Uninitiated!—————————
1.模型解析
首先应该看清楚这个model的真实面目,如下图:

对于文中Figure4,展开来应该如上图,之前我对于Graph Model其实具体接触比较少,对于Figure4那样画成Plate还是有误导性(主要是会误以为W只是一个随机变量),在这个图里Plate被展开了,所以我就随便用虚线替代实线,对于该图展开后的解释如下:
1.每一个文档有一个Label(j),是文档的class,同时
θ0
和
θ1
是和
Lj
对应的,如果
Lj=1
则对应的就是
θ1
2.在Gibbs Sampling中,所有的圆圈都是要被sample的,也就是每一个
Lj
都会被算作一个
zi
(在Gibbs Sampling表达式里面
z(t+1)i∼P(Zi|z(t+1)1,…,z(t+1)i−1,z(t)i+1,…)
中的随机变量z),同理,每一个
wjk
也是一个
zi
,只不过在具体sampling的时候,
Lj
是会被单独sample的,而
wjk
是整体sample的,这个会在后面讲到。
3.在这个model中,Gibbs Sampling所谓的P(Z),就是产生图中这整个数据集的联合概率,也就是产生这N个文档整体联合概率,还要算上包括超参
γ
产生具体
π
和
θ
的概率。所以最后得到了上图中表达式与对应色彩。
2.联合概率公式推导
分别对红色、绿色、蓝色、紫色部分求表达式,得到如下结果:
1)红色部分:这个是从beta分布sample出一个伯努利分布,伯努利分布只有一个参数就是
π
,不要normalization项(要求的是整个联合概率,所以在这里纠结normalization是没有用的),得到:
P(π|γπ1,γπ0)∝πγπ1−1(1−π)γπ0−1
2)绿色部分:这里L是一整个向量,其中值为0的有C0个,值为1的有C1个,多次伯努利分布就是二项分布啦,因此:
P(L|π)∝πC1(1−π)C0
3)蓝色部分:对于0类和1类的两个
θ
都采样自参数为
γθ
的狄利克雷分布,注意所有这些都是向量,有V维,每一维度对应一个Word。根据狄利克雷的PDF得到以下表达式,其实这个表达式有两个,分别为
θ0
和
θ1
用相同的式子采样:
P(θ|γθ)∝∏i=1Vθγθi−1i
4)紫色部分:这部分,首先要求对于单独一个文档n,产生所有word也就是
Wn
的概率。假设对于某个文档,
θ=(0.2,0.5,0.3)
,意思就是word1产生概率0.2,word2产生概率0.5,假如这个文档里word1有2个,word2有3个,word3有2个,则这个文档的产生概率就是(0.2*0.2)*(0.5*0.5*0.5)*(0.3*0.3)。所以按照这个道理,一个文档整个联合概率如下:
P(Wn|L,θLn)=∏i=1VθWnii
上面这个概率是针对单个文档而言的,把所有文档的这些概率乘起来,就得到了紫色部分:
P(Cx|L,θx)=∏n∈Cx∏i=1VθWnix,i=∏i=1VθNCx(i)x,i
其中x的取值可以是0或1,所以
Cx
可以是
C0
或
C1
,当x=0时,
n∈Cx
的意思就是对于所有class 0中的文档,然后对于这些文档中每一个word i,word i在该文档中出现
Wni次
,求
θ0,i
的
Wni
次方,所有这些乘起来就是紫色部分。后面那个表达式是规约后得到的结果,
NC0(i)
的意思就是word i出现在calss为0的所有文档中的总数,同理对于
NC1(i)
。
最后把上述4部分乘起来,就得到整个模型的联合概率。不再赘述,只是说明文中从式(29)跳到(30),以及式(31)到式(32)的计算,都用到了Beta分布与二项分布共轭的性质,以及多项分布与狄利克雷分布共轭性质,这些可以从PRML2.2和2.3中读到【1】。
3.将隐含变量
π
积出
为了方便,可以对隐含变量
π
进行积分,最后达到消去这个变量的目的。
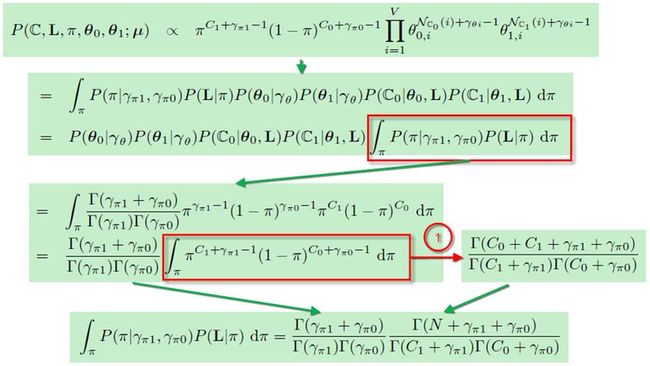
图中带圈的(1)作者是直接通过Beta分布的Normalize Constant得出的,也就是和【1】是同一个道理。
4.吉布斯采样框架
包含三个步骤,按照顺序(1),(2),(3)进行
(1)对所有L变量采样一轮。即整个数据集合有N个文档,也就是有N个L实例,依次对每一个文档j,采样
Lj
:
P(Lj)(t+1)=P(Lj|L(t+1)1,…,L(t+1)j−1,L(t)j+1,…L(t)N,C(t),θ(t)1,θ(t)0;μ)
注意表达式后面那部分的样子,在条件概率中,没有
Lj
项,同时
Lj
之前的项是(t+1),就是基于已经采样过的
L1→Lj−1
的结果,而
Lj
之后的所有项都是基于(t)轮,也就是前一轮采样的结果。
(2)对
θ0
采样,可以发现下式中是没有
θ0
的,这就是Gibbs采样的要求:
P(θ0)(t+1)=P(θ(t+1)0|L(t+1)1,L(t+1)2,…,L(t+1)N,C,θ(t)1;μ)
(3)对
θ1
采样:
P(θ1)(t+1)=P(θ(t+1)1|L(t+1)1,L(t+1)2,…,L(t+1)N,C,θ(t+1)0;μ)
对于其他变量,
γ
为超参数,是人为设定的,W为观察变量,不需采样。
然后就要求出
P(L(t+1)j|L(−j),C(−j),θ0,θ1;μ)
的表达式,这里有一些关键的理解,首先求出这个表达式之后要怎样对
Lj
进行采样。事实上他的具体做法是这样的,有了
P(Lj)(t+1)
的表达式,我们要把
Lj=0
和
Lj=1
两个情况带入表达式,分别求出L为0和1的概率,这样就可以为
L(t+1)j
挑选一个新的值。怎么挑这个值,举例来说,如果
P(L(t+1)j=0)=0.2
,
P(L(t+1)j=1)=0.3
,那么就可以产生一个伯努利分布,其参数:
μ=P(Lj)(t+1)被赋值为0的概率=P(Lj=0)/(P(Lj=0)+P(Lj=1))=0.4
然后我用random函数从uniform distribution产生一个随机数r,如果r<=0.4,则将
L(t+1)j
赋值为0,否则赋值为1。
在这里不累赘写L的概率表达式了,记录一些关键内容。首先,计算
P(L(t+1)j)
的时候,是要查看
L(t)j
的值的,因为我们要把文档
Lj
从原来的集合中去掉,那么如果
L(t)j==1
,就要从C1中扣除1,否则要从C0中扣除1。那么式(45)在计算的时候,为什么分子分母会被越成这个样子?因为对于特定的
L(t)j
等于0或1代入时(也就是Lj上一个状态的值),C0和C1只有其中一个会被减去1,而另外一个不变,不变化的那个就被分子分母约掉了!所以(45)中只剩下
Cx
,也就是被减了1的那个C。同理,对于式(47),看起来好像是
θ0
和
θ1
乘在一起,其实只有其中一个会被减去L中的词的个数,另外一个不变的就全部约掉了,所以最后只会剩下式(48)。
另外,对于式(52),其实作者还是没有写清楚,怎么从伽马分布
Gamma(αi,1)
采样yi呢?呵呵,这个正好在PRML11.1.2 Reject Sampling里面有的哦~
最后的最后,文章给出了很关键的理解:
P(Lj=x|L(−j),C(−j),θ0,θ1;μ)=Cx+γπxN+γπ1+γπ2−1∏i=1VθWjix,i
这个式子中,前半部分其实只有Cx是变量,所以如果C0大,则
P(L(t+1)j=0)
的概率就会大一点,所以下一次Lj的值就会倾向于C0,反之就会倾向于C1。而后半部分呢,是在判断当前
θ
参数的情况下,整个文档的likelihood更倾向于C0还是C1。

