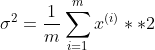吴恩达神经网络和深度学习第二课笔记-week1-超参数调试、正则化以及优化
一、数据集（P1）
数据集分类：
- 训练数据集（training set）：在训练集上之下训练算法，进行模型拟合
- 交叉验证集（corss validation set / development set / dev set）：通过交叉验证集来选择最好的模型（评估不同算法、调整模型超参数等），经过验证后，选定最终模型
- 测试集（test set）：对最终所选定的神经网络系统做出无偏评估，用于评估模型的泛化能力
各数据集的占比：
- 传统的划分比例（1万条数据及以下）：训练集、交叉验证集、测试集各占60%、20%、20%；如果没有交叉验证集，则训练集和测试集各占70%、30%
- 大数据时代（百万级别数据）：只需要1万条数据用于交叉验证不同算法，因此比例为98%，1%，1%；超过百万数据的情况下，用于验证和测试的数据占比更低，例如：99.5%、0.4%、0.1%
两点注意：
- 没有测试集也可以，即不对模型做无偏评估。在训练集上训练，尝试不同的模型框架，在验证集上评估这些模型，然后迭代并选出适用的模型。因为验证集中已经涵盖测试集数据，因此不再提供无偏性能评估。
- 三种验证集最好是来自于同一分布，例如：训练集数据来自于用户上传，那么交叉验证或者测试集数据也要来自于用户上传，而不能是从网络上下载的高清图片。
二、偏差和方差（P2-P3）
直观感受，从左到右依次是 高偏差（欠拟合），合适，高方差（过拟合）：
偏差（bias）：反映模型在样本上的输出与真实值之间的误差，即模型本身的精准度，通过比较最优误差和训练集误差得出是否是高偏差，偏差高反映出欠拟合。
方差（variance）：反映模型每一次在验证集上的输出结果与模型输出期望之间的误差，即模型的稳定性，通过比较验证集误差和训练集误差得出是否是高方差，方差高反映出过拟合。
例如：针对一个识别猫的图片，人眼的识别误差是0%，这是基本误差（Base Error）。那么，训练集误差如果高于0%太多，就是欠拟合（高偏差）。但如果基本误差本身就高（比如15%），训练集误差也是15%，那么这种就是合理的，并不是欠拟合。
下图展示了最优误差0%时的训练集误差和交叉验证集误差的几个例子：
| 情况1 | 情况2 | 情况3 | 情况4 | |
| 训练集误差 | 1% | 15% | 15% | 0.5% |
| 交叉验证集误差 | 11% | 16% | 30% | 1% |
| 判断结论 | 低偏差，高方差 | 高偏差，低方差 因为验证集错误率和训练集一致 |
高偏差，高方差 | 低偏差，低方差 |
高偏差说明欠拟合，可以采取的应对方法：
- 更大的网络（bigger network）
- 花费更多时间训练算法
- 采用更合适的神经网络架构（neural network architecture）
总之，解决高偏差是首要问题，至少要拟合训练集，将偏差降低到可接受的数值，然后再考虑高方差问题。
高方差说明过拟合，可以采取的应对方法：
- 采用更多的训练数据
- 正则化（regularization）
- 采用更合适的神经网络架构（neural network architecture）
反复调整网络，直至方差和偏差都在可接受范围内。
三、正则化方法（P4-P8）
正则化可以防止过拟合。
正则化方法：
- L2正则化
- Dropout
- 数据扩增（Data augmentation）
- Early Stop
（一）L2正则化（P4）
L2正则化在成本函数J(w^[1],b^[1], ..., w^[L],b^[L])后面加上一项 lambd/2m……，其中，lambd是L2参数，也属于超参数，通过交叉验证集来配置lambd
L2正则化也称作权重衰减（weight decay），上图绿色字体部分说明了原因：通过L2正则化，权重w在每次更新时都比不用正则化更新的值小了(alpha*lambd / m) 倍的w，即相当于给矩阵乘以了(1 - alpha*lambd / m)倍的权重，该系数小于1。简单来说，L2正则化避免了权重w过大。
上图中的连续两个求和符号貌似写反了……
为什么L2正则化可以避免过拟合？
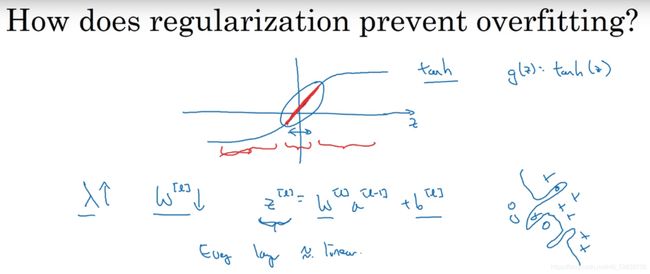
直观理解：当L2参数lambd非常大时，权重w趋近于0，即对应的神经元的权重趋于0，相当于消除了这些单元的影响，导致神经网络变小，小到如同一个逻辑回归单元（logistic regression），但深度依然很大（如下图左上角的神经网络），从而使一个过拟合的网络更接近于高偏差状态。而一个lambd的中间值，就可以使网络just right。权重小的神经元的影响变得更小。
另一个角度的直观理解：如下图，假设激活函数是a^[l]=tanh(z^[l])，当权重w由于L2正则化影响变小时，z^[l]=w^[l]a^[l-1]+b^[l]也很小，使tanh()函数都在进行线性计算，那么神经网络是一个线性网络，只能计算线性函数，不适用于复杂的决策，更不会过拟合。
b的影响可以忽略，因为它是标量。
（二）Dropout正则化（P6-P7）
Dropout（随机失活）概述：遍历神经网络的每一层，设置消除神经网络中节点的概率，消除某些节点和从该节点进出的连线，最后得到一个节点更少，规模更小的网络，然后back propagation方法进行训练。对于每个训练样本，都采用一个精简后的神经网络来训练它。对不同的训练样本，消除的单元也不同。
Dropout的一种常用实现方法：反向随机失活（inverted dropout），步骤如下：
以神经网络第三层（l=3）为例，神经单元被保留的概率用keep-prob表示，设keep-prob=0.8
首先，生成一个和a^[3]同形状的矩阵d3，用来指示对应的单元是消除还是保留：
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep-proba3表示第三层的a值，即a^[3]；
d3是 一个形状为 (a3.shape[0], a3.shape[1]) 的矩阵，矩阵里每个元素要么是True（rand生成的随机数小于keep-prob），要么是False（rand生成的随机数大于keep-prob）
然后，对a^[3]执行随机失活，即将a^[3]的某些元素值变为0：
a3 = np.multiply(a3, d3) # a3 *= d3Python会把True和False自动翻译为1和0，因此乘法有效。
最后，调整a^[3]中被保留的单元的值，确保a^[3]在把某些神经单元变成0后的期望不变：
a3 /= keep-prob注意：Dropout只在训练时使用，在测试阶段不使用Dropout，因为在测试阶段，不希望输出结果是随机的；如果在测试阶段使用Dropout，预测会受干扰。
为什么Dropout正则化可以避免过拟合？
直观感受：不能给任何神经单元加上太多权重，因为它有可能被随机清除，即不把所有赌注放在一个节点上。Dropout和L2正则化功能类似，Dropout也会压缩权重，它会使权重趋于分散，不会使某个权重过大。
不同层的keep-prob可以变化，如下图，对参数多的某一层，keep-prob可以设得较小，对于参数少的层，keep-prob可以为1，表示不消除任何单元。如下图：
Dropout在计算机视觉领域用得较多，因为计算机视觉中的输入量非常大，输入太多像素作为特征，以至于没有足够的数据存在产生过拟合现象。
（三）其他正则化方法（P8）
- 数据扩增（Data augmentation）：对图片进行旋转、扭曲裁、翻转、缩放、平移、剪切，色彩抖动、数据合成等方式扩充训练集，虽然这些方式存在数据冗余，但聊胜于无。
- 早停（Early stopping）
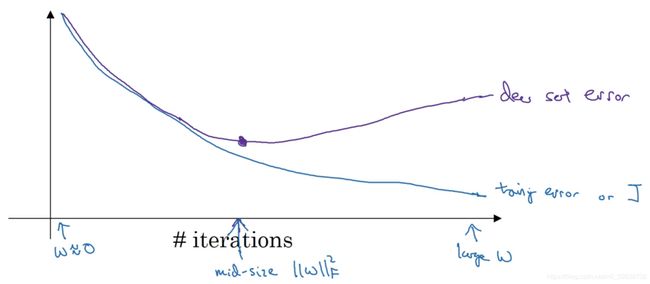
紫色曲线表示交叉验证集误差，蓝色曲线表示训练集误差。
随着迭代进行，w值从最初的趋于0的小数变得越来越大，最终，当紫色曲线出现拐点开始上升时，过拟合现象出现。Early stopping就是提前停止迭代，得到一个中等大的权重w，避免出现过拟合。
Early stopping有一个缺点：降低成本函数的同时必须时刻关注验证集上的误差情况，这两项任务同时进行，为了避免过拟合而停止梯度下降时，也停止了优化成本函数。Early stopping导致我们不能采取不同方式来解决这两个问题。Early stopping的优点是只运行一次梯度下降，就能找到w的较小值、中间值和较大值。而L2正则化带来了额外的超参数lambd，必须尝试很多lambd的值，这导致高昂的计算代价，因此采用L2正则化方法的计算时间较长。
四、归一化输入（P9）
目的：确保所有输入特征的取值范围和分布都差不多，例如：避免x1取值在0到1，而x2取值在1到1000这种情况。
训练集的输入归一化分为两个步骤：
（一）零均值化（zero out the mean）：
这一步求所有样本在特征x上的均值
X是一个向量，等于每个训练数据x减去均值
完成以上操作后，就完成了零均值化（从左图变到了右图）
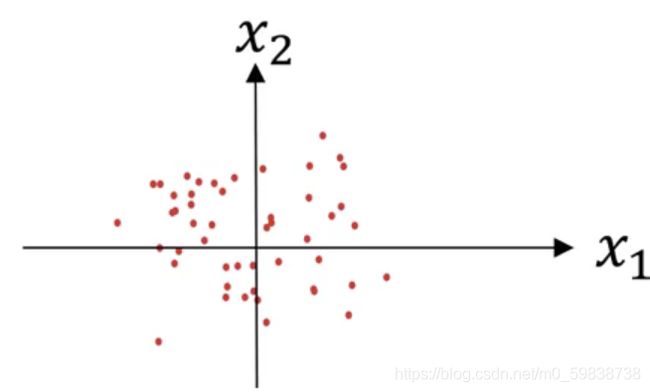
（二）归一化方差（normalize the variances）
上图中可看出：x1的方差比x2大很多（x1比x2分散），现在要做的就是让它们方差一样。
是一个向量，它的每个特征都有方差；
已经完成零均值化，因此，
就是方差。
完成这步后，x1和x2的方差都是1，分布如下图：
注意：和
是从训练集中计算获得，在归一化测试集时，也需要用和训练集相同的和，确保训练集和测试集的归一化是相同的。
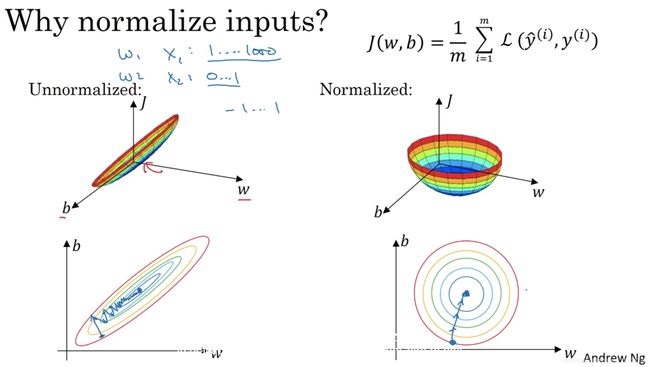
为什么要归一化数据？
使代价函数J优化起来更加快速。下图是非归一化和归一化的代价函数对比图：
五、梯度消失与梯度爆炸（P10-P11）
设一个神经网络的层数很大，如L=150：
当选取的初始权重比1大时，经过L层的神经网络计算后，神经网络的激活函数将爆炸式增长；
当选取的初始权重比1小时，经过L层的神经网络计算后，神经网络的激活函数将以指数级递减；
以上规律也适用于与层数L相关的导数或梯度函数
解决方案：为神经网络进行合理的权重初始化，如：Xavier初始化。