机器学习之Python Sklearn——线性回归
这里重点学习一下回归算法
机器学习基础
机器学习 vs. 传统编程

三种类别
根据使用场景不同,有可以划分为三大类
监督学习
监督学习是根据已知的方法和规律,对新样本进行分类和预测。
监督学习就好比学生在学校学习各种知识和理论的过程。整个过程是在老师的监督下完成,所学知识的应用体现在平时的测试中,并且可以通过对比“标准”答案来不断改进和巩固学习成果,在下一次的测试中取得更好的成绩(预测效果)。根据目的不同,可以有分类和回归(预测)两种:
- 分类 —— 根据事物特征将其划分到已知的类别。
- 根据事物的特征,将新遇到的事物(新样本)归类到已知的某个类别。
- 回归(预测)—— 根据事物的特征和预测将来的发展趋势。
- 根据事物的特征和发展规律,预测将来的发展趋势。
非监督学习
非监督学习与监督学习正好相反,在过程中并不清楚有哪些特征标签,而是通过对样本的观察、分析和总结,去发现其中的特征,从看似杂乱无章的数据中发现共性。然后对新样本进行归类。
归类/聚类(clustering)—— 对大量看似无特征的样本进行分类。
经常会说非监督学习是归类或聚类(clustering)。与分类不同,聚类在划分之前并不知道有哪些类别,以及类别的特征,而是通过对样本的各种特征进行分析,将相似的样本划分为一组,进行“物以类聚”的划分。是一个从无到有的发现过程。
半监督学习
介于监督和非监督学习之间。是基于监督学习获得理论和知识,对非监督学习的样本(无特征标签)进行分类。可以理解为我们走出学校以后根据在课堂上学到的知识和理论,对生活中遇到的事物进行分类和预测。
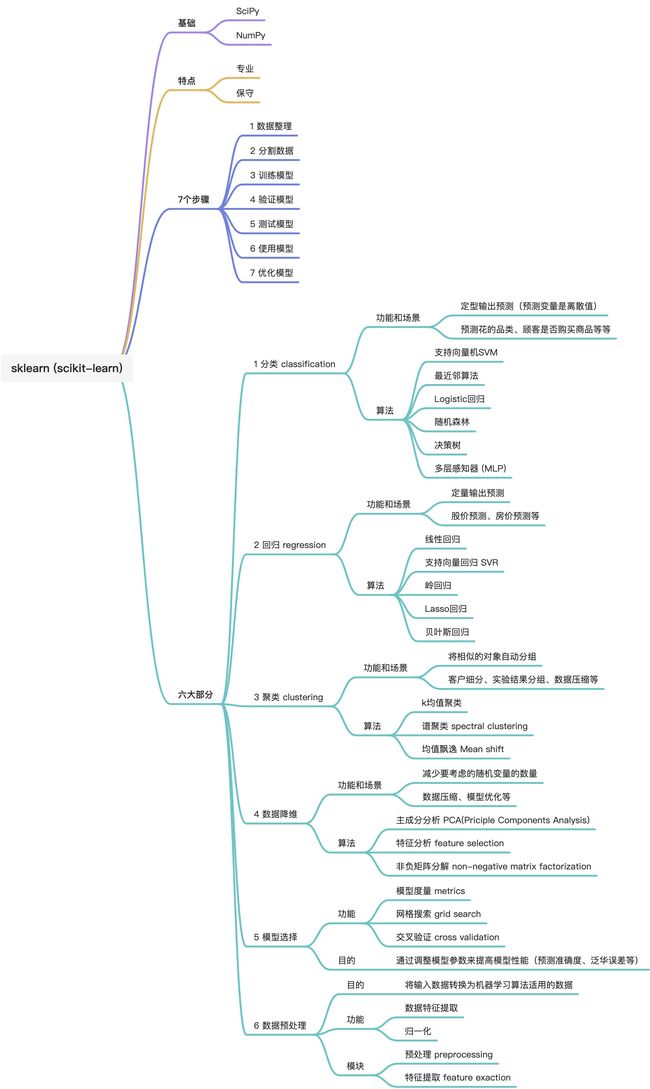
Python sklearn (scikit-learn)
Scikit-learn是一个用于Python的免费开源机器学习库。
机器学习三大步骤
机器学习的本质就是让机器使用特定的算法对输入数据进行类似人的智能学习(找规律),根据同样的模型对新样本进行进行预测。具体到python中的sklearn,是通过一下三大步骤实现的。
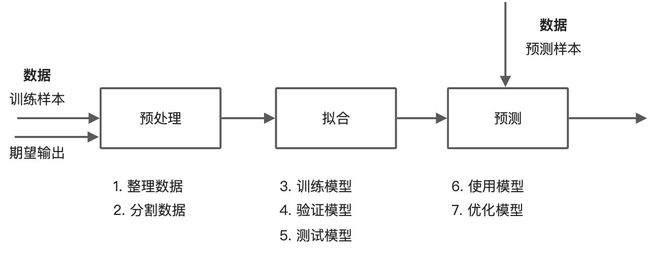
- 准备数据——对输入数据进行预处理
- 选择、训练和测试模型——使用处理后的样本数据,针对特定模型进行拟合、训练
- 模型的选择,可以根据要解决的问题和使用场景,scikit-learn提供了一张图(选择正确的估计器)来详细描述模型选择的流程,最终指向机器学习的集中主要使用场景,回归、分类和聚类,以及scikit-learn提供的数据降维方法。

- 使用模型预测——使用训练后的模型对新样本进行预测,并根据预测结果过进一步优化
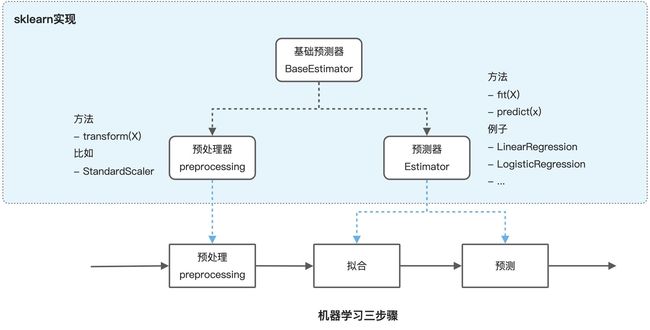
scikit-learn (sklearn) 实现
sklearn中内置了常用的机器学习算法和模型,以及基本的预处理方法。分别由**预测(估计)器(estimator)和预处理器(preprocessing)**实现,并且它们继承自同一个基础预测器。
转换器和预处理器
预处理器和转换器主要负责对原始数据的预处理和转换,从而消除不同数据之间的绝对差异。
from sklearn.preprocessing import StandardScaler
# ...
# X = [...]
StandardScaler().fit().transform(X)
预测器
sklearn中提供的数十种内置机器学习算法和模型,都通过估算器提供。可以通过引入相应的估算器来使用对应的模型。
from sklearn.ensemble import RandomForestClassifier
# 初始化估算器
clf = RandomForestClassifier(random_state=0)
# 使用训练数据进行模型拟合
clf.fit(X, y)
# 预测
clf.predict(...) #
管道
管道用来将转换器和预测器组合成一个同一的对象,表示一个完整的数据流处理过程(管道)。然后使用管道的fit和predict来进行训练和预测。同时,使用管道还可以防止数据泄露。
from sklearn.preprocessing import StandardScaler # 预处理器
from sklearn.linear_model import LogisticRegression # 预测器
from sklearn.pipeline import make_pipeline # 管道
# 创建管道
pipe = make_pipeline(
StandardScaler(),
LogisticRegression(random_state=0)
)
#准备数据...
# 像使用预测器一样使用管道
# 1) 训练整个pipeline
pipe.fit(X_train, y_train)
# 2) 使用管道预测
pipe.predict(X_test)
# ...
模型评估
针对不同类型的算法和模型,对应评估指标也不相同。
回归算法指标
回归算法的核心思想是评估预测值和观察值之间的误差。从最原始的残差(residual)到基于残差的各种变形,以便后续的数学运算和处理。
- Mean Absolute Error 平均绝对误差:对残差做绝对值处理,避免残差正负导致的相互抵消。
- Mean Squared Error 均方误差:为了便于求导,对平均绝对误差进行平方。
- Root Mean Squared Error 均方根误差:如果目标变量的量纲保持一致,可以对均方误差进行开放。
- Coefficient of determination 决定系数:进一步去除对量纲的依赖。
分类算法指标
相比较回归算法的各种残差指标,分类算法更多的则是关注分类的精度,即预测正确的样本数量占总预测样本的比例。然后,预计不同的场景,从不同角度来看精度对结果的影响。
- Accuracy 精度:每一个分类中预测正确的样本数占总样本的比例。
- 混淆矩阵 Confusion Matrix
- 准确率(查准率) Precision
- 召回率(查全率)Recall
- Fβ Score
- AUC Area Under Curve
- KS Kolmogorov-Smirnov
关于各个指标的详细说明,可以参考知乎——机器学习评估指标。
参数搜索
所有预测器都有可以调整的参数,也叫超参数。其特指不能通过学习得到的参数。在使用各种不同模型时,需要将超参数作为参数传递给预测器。
sklearn中提供了在参数集中搜索最佳超参数的方法,其基于最佳交叉验证(CV, Cross-Validation)分数获取对应的超参数。sklearn中最简单的方法是调用cross_val_score函数。
估算器中的任意参数都可以通过参数搜索来获得最佳参数。
参数搜索的基本要素
- 参数搜索方法
- 评估方法
sklearn中两种抽样搜索最佳参数的方法:
GridSearchCV 网格搜索方法
计算参数集中所有参数的组合。GridSearchCV通过使用param_grid参数来指定参数候选值。
例如下边的例子指定搜索两个参数候选值。通过GridSearchCV的fitting接口拟合后,会对所有候选参数进行评估,保留最优参数组合。
# 选择模型
clf = ...
# 指定网格搜索的参数
param_grid = [
{'C': [1, 10, 100, 1000], 'kernel': ['linear']},
{'C': [1, 10, 100, 1000], 'gamma': [0.001, 0.0001], 'kernel': ['rbf']},
]
# 运行网格搜索
grid_search = GridSearchCV(clf, param_grid=param_grid)
# ...
grid_search.fit(X, y)
RandomizedSearchCV 随机搜索方法
从具有制定分布的参数空间中抽样出定量的参数候选。RandomizedSearchCV会在指定范围内,使用某个特定分布抽取参数值进行评估。用字典形式来指定参数的具体抽样范围,针对每一个参数,可以指定
- 具体的参数
- 采样分布——可以使用scipy.stats模块,其中包含了很多采样分布,如expon,gamma,uniform或者randint。
- 离散选项列表
例子
# 选择模型
clf = ...
# RandomizedSearchCV 参数设置示例
param_dist = {
'C': scipy.stats.expon(scale=100), # 取值分布
'gamma': scipy.stats.expon(scale=.1),
'kernel': ['rbf'], # 离散列表
'class_weight':['balanced', None] # 离散列表
}
# 运行随机搜索
n_iter_search = 20
random_search = RandomizedSearchCV(clf, param_distributions=param_dist,
n_iter=n_iter_search)
# ...
random_search.fit(X, y)
评估方法(指标)
参数搜索默认使用估计器的score函数来评估参数的设置。默认为
- sklearn.metrics.accuracy_score 用于分类
- sklearn.metrics.r2_score 应用于回归
当然,sklearn还提供了其它一些评估函数可供不从场景使用。同时,也可以将多种评估指标结合起来使用。
回归算法
从sklearn模型流程可以很清楚得看到回归算法的使用场景。

使用场景
- 样本数大于50
- 需要预测将来的某个具体数据(而不是对数据分类)
然后根据样本数据数据和特征标签的特点选择对应的算法
- 样本数大于100K时,推荐使用SGDRegressor
- 样本数小于100K时,则推荐使用Ridge, Lasso, 或者ElasticNet等;然后根据样本数据特征标签的权重,进行进一步选择。
- 如果样本数据的特征标签同等重要,可以选择RidgeRegression或SVR;
- 如果样本数据的某些特征更重要,对结果影响更大,可以使用Lasso和ElasticNet;
回归分析(Regression Analysis)
在搞清楚线性回归之前,我们首先要弄明白什么是回归分析。在统计学中,是指确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
按照涉及的变量多少,可以分为一元回归和多元回归;按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
线性回归(Liner Regression)基础
线性回归假设目标值(因变量)是特征值(自变量)的线性组合。线性回归使用最佳的拟合直线在因变量( Y Y Y)和一个或多个自变量( X X X)之间建立一种关系。因变量是连续的,自变量可以是连续的也可以是离散的,回归线的性质是线性的。
在数学中,即为由特征值组成的多元一次方程。
Y = b + w 1 x 1 + . . . + w p x p + ϵ Y=b+w_1x_1+...+w_px_p+\epsilon Y=b+w1x1+...+wpxp+ϵ
如果将自变量表示为 X = ( x 1 , . . . x p ) X=(x_1,...x_p) X=(x1,...xp),系数表示为 W = ( w 1 , . . . , w p ) W=(w_1, ..., w_p) W=(w1,...,wp),就能明白为什么它叫线性回归了。
Y = b + W T X + ϵ Y=b+W^TX+\epsilon Y=b+WTX+ϵ
其中 W W W是回归线的斜率, w 0 w_0 w0则表示回归线在Y轴上的截距, ϵ \epsilon ϵ表示误差项。
上边的表示中,我们默认自变量和因变量都是多元的。这里我们限制因变量的个数为一个,则可以直接表示为
y = b + W T X + ϵ y=b+W^TX+\epsilon y=b+WTX+ϵ
线性回归就是通过各种算法去找到这样一个多元一次方程 y ^ ( x ) = b + w X \hat{y}(x)=b+wX y^(x)=b+wX,使其尽量接近观真实值 y y y(残差 ϵ \epsilon ϵ尽量小)。而拟合的过程,就是去不断优化和估计方程的斜率系数,所以也叫“回归系数(coefficient)”。
这里要注意模型偏差bias和**残差(噪声)**的区别。
- 偏差 b b b——指排除噪声影响下,预测结果与真实值之间的差异。其主要是由模型的拟合度不够导致的(不是随机的,并且可通过一定的特征工程进行预测)。
- 残差 ϵ \epsilon ϵ——预测结果与真实值之间的差异。在模型完全拟合的情况下,与真实值之间的差异,因此可以理解为噪声(随机、不可预测的)。
预测值和真实值的距离
那么,如何衡量预测的准确性,即衡量预测值 y ^ ( x ) \hat{y}(x) y^(x)与真实值 y y y之间的差异呢?最直观的方法就是看真实值和预测值之间的差(残差)。回归模型的目的就是使模型预测出来的值无限接近真实值(测量值)。
ϵ ^ = y − y ^ ( x ) \hat{\epsilon} = y - \hat{y}(x) ϵ^=y−y^(x)
但是在实际预测中,残差值有正有负,不可能直接使用残差之和最小的方式来衡量一种方法的好坏。
因此,整个回归问题的本质,就是使用均方误差,求使 D D D最小时的 W W W和 d d d。
D = E ( y − y ^ ( x ) ) 2 D=E(y-\hat{y}(x))^2 D=E(y−y^(x))2
1. 残差平方和SSE
由于残差本身有正有负,故可以使用平方和来避免正负抵消问题。
d i s t ( P i , P j ) = ∑ k = 1 n ( P i k − P j k ) 2 dist(P_i, P_j) = \sum_{k=1}^n(P_ik-P_jk)^2 dist(Pi,Pj)=∑k=1n(Pik−Pjk)2
问题:
- 使用平方后会放大(差>1)部分的误差,同时缩小(-1<差<1)部分的误差;
- 当不同维度的度量差异很大时无法处理;
2. 欧氏距离
为了解决误差平方和的问题,我们可以使用欧式距离。
d i s t ( P i , P j ) = ∑ k = 1 n ( P i k − P j k ) 2 dist(P_i, P_j) = \sqrt{\sum_{k=1}^n(P_ik-P_jk)^2} dist(Pi,Pj)=∑k=1n(Pik−Pjk)2
问题:
- 求解麻烦;
- 不同问题的度量差异很大时无法处理;
3. 曼哈顿距离
曼哈顿距离直接使用绝对值来消除根号开方的求解麻烦问题。
d i s t ( P i , P j ) = ∑ k = 1 n ∣ P i k − P j k ∣ dist(P_i, P_j) = \sum_{k=1}^n\vert P_ik-P_jk\vert dist(Pi,Pj)=∑k=1n∣Pik−Pjk∣
问题:
- 不是连续函数,求导很麻烦,计算不方便,只能计算垂直、水平距离
适合场景:数据稀疏(自带归一化处理)
4. 马氏距离(Mahalanobis Distance)
马氏距离是对欧式距离的另外一种修正,修正了欧氏距离中各个维度尺度不一致且相关的问题。
d i s t ( P i , P j ) = ( P i k − P j k ) T Σ − 1 ( P i k − P j k ) dist(P_i, P_j) = \sqrt{(P_ik-P_jk)^T\Sigma^{-1}(P_ik-P_jk)} dist(Pi,Pj)=(Pik−Pjk)TΣ−1(Pik−Pjk)
马氏距离已经不像前边的几种那么好理解,具体推导过程可以参考马氏距离。总之,其较好的解决了不同维度尺度不一致且相关的问题。
5. 其它
其它还有一些距离如汉明距离(Hamming Distance)、编辑距离(Levenshtein Distance)等,这里不做一一说明。
普通最小二乘法(Ordinary Least Square, OLS)
最小二乘法直接使用残差的平方和作为衡量标准,通过拟合 W W W使残差 ϵ \epsilon ϵ的平方和最小。数学上表示为下边的形式:
m i n ∥ X w − y ∥ 2 2 min{\Vert Xw-y\Vert _2^2} min∥Xw−y∥22

在sklearn的线性回归模型LinearRegression中,使用 f i t ( ) fit() fit()函数拟合模型,并在模型的coef_中存储拟合后的相关系数 w w w。
import numpy as np
from sklearn import datasets, linear_model
# ...准备数据,选择特征列,拆分训练、测试数据集..
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
print("Coefficients: \n", regr.coef_)
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))
非负最小方差
在最小二乘法法返回的系数中,默认是不会对系数的正负进行限制的。但是在实际问题中,很多时候我们需要所有的相关系数非负,例如频次、商品价格等。这时候可以直接设置LinearRegression的positive参数为True来限制相关系数的正负。
from sklearn.linear_model import LinearRegression
reg_nnls = LinearRegression(positive=True)
y_pred_nnls = reg_nnls.fit(X_train, y_train).predict(X_test)
r2_score_nnls = r2_score(y_test, y_pred_nnls)
print("NNLS R2 score", r2_score_nnls)
问题
普通最小二乘的系数估计依赖于特征的独立性。当特征相关且设计矩阵的列之间具有近似线性相关性时, 设计矩阵趋于奇异矩阵,最小二乘估计对观测目标的随机误差高度敏感,可能产生很大的方差。例如,在没有实验设计的情况下收集数据时,就可能会出现这种多重共线性的情况。
过拟合(Overfitting)和欠拟合(Underfitting)
过拟合和欠拟合是使用实际数据进行分析时可能会遇到的两种基本问题。

- 欠拟合——指模型在训练集中的表现就很差了,经验误差很大。
欠拟合出现的原因是模型复杂度太低,比如自变量太少等。针对欠拟合,要做的就是增大模型复杂度,增加自变量,或者改变模型(线性到非线性)等。
- 过拟合——指模型在训练集中表现良好,而测试集中表现很差,即泛化误差大于了经验误差,拟合过度,模型泛化能力降低,只能够适用于训练集,通用性不强。
过拟合的原因是模型复杂度太高,或者训练数据集太少,比如自变量过多等。针对过拟合,除了增加训练集数据外,正则化就是常用的一种处理方法。
正则化
- 正则化(Regularization) 是机器学习中对原始损失函数引入额外信息,以便防止过拟合和提高模型泛化性能的一类方法的统称。也就是目标函数变成了原始损失函数+额外项,常用的额外项一般有两种,英文称作ℓ1−ℓ1−norm和ℓ2−ℓ2−norm,中文称作L1正则化和L2正则化,或者L1范数和L2范数(实际是L2范数的平方)。
- L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓惩罚是指对损失函数中的某些参数做一些限制。对于线性回归模型,使用L1正则化的模型叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
关于正则化的更多详细理解可以参考深入理解L1、L2正则化,以及机器学习中正则化项L1和L2的直观理解。
岭(Ridge)回归(L2正则化)
针对最小二乘法存在的一下问题,岭回归则计算一个带惩罚项的残差平方和。
m i n ∥ X w − y ∥ 2 2 + α ∥ w ∥ 2 2 min{\Vert Xw-y\Vert _2^2}+\alpha\Vert w \Vert _2^2 min∥Xw−y∥22+α∥w∥22
其中 ∥ w ∥ 2 2 \Vert w \Vert _2^2 ∥w∥22为回归系数向量的L2范数(所有参数的平方和)。使用复杂度参数 α ≥ 0 \alpha \ge0 α≥0来控制收缩程度:值越大,收缩程度越大,对应的回归系数对共线性的容忍程度也就越大。至于为什么L2正则化能防止过拟合,可以参考深入理解L1、L2正则化。

在sklearn中,可以通过指定alpha参数来设定 α \alpha α。
from sklearn import linear_model
# 指定alpha的岭回归
reg = linear_model.Ridge(alpha=.5)
# 拟合
reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
# ...
Lasso回归(L1正则化)
Lasso回归与Ridge岭回归类似,都是在普通最小二乘法基础上的正则化处理。目标函数在数学上表示为
m i n 1 2 n s a m p l e ∥ X w − y ∥ 2 2 + α ∥ w ∥ 1 min{\frac1{2n_{sample}}\Vert Xw-y\Vert _2^2}+\alpha\Vert w \Vert_1 min2nsample1∥Xw−y∥22+α∥w∥1
其中 ∥ w ∥ 1 \Vert w \Vert _1 ∥w∥1为回归系数向量的L1范数(所有参数绝对值之和)。
特征选取与压缩感知
特征选取就是对样本进行稀疏表示的过程。而Lasso正好就是估计稀疏系数的线性模型,因为它倾向于给出非零系数较少的解,从而有效地减少了给定解所依赖的特征数。至于为什么L1正则化能减少给定解所依赖的特征数,可以参考深入理解L1、L2正则化。
所以说,Lasso 及其变体是压缩感知领域的基础。关于稀疏表示,参考 机器学习基础——稀疏表示。
稀疏表示
任意一个信号都可以在一个过完备字典上稀疏线性表出。这样,一个信号被分解为有限个信号的线形组合的形式我们称之为稀疏表示。表达为公式为:
y = D_α_ s.t.||α||0 < σ
Elastic-Net弹性网络回归(L1+L2正则化)
弹性网络回归是一个综合了Ridge回归和Lasso回归两种惩罚因数的单一模型:一个因素与L1范数成比例,另外一个因数与L2范数成比例。其目标函数表示为
m i n 1 2 n s a m p l e ∥ X w − y ∥ 2 2 + α β ∥ w ∥ 1 + α ( 1 − β ) 2 ∥ w ∥ 2 2 min{\frac1{2n_{sample}}\Vert Xw-y\Vert _2^2}+\alpha\beta\Vert w \Vert_1+\frac{\alpha(1-\beta)}{2} \Vert w \Vert_2^2 min2nsample1∥Xw−y∥22+αβ∥w∥1+2α(1−β)∥w∥22
从上边的公式可以看出,ElasticNet使用时需要提供 α \alpha α和 β \beta β两个参数。其中 β \beta β的参数名称为l1_ratio。
当多个特征存在相关时,弹性网是很有用的。Lasso很可能随机挑选其中之一,而弹性网则可能兼而有之。
预估正则化参数——贝叶斯回归
主要用于预估正则化参数:正则化参数不是应意义上的设置,而是根据数据进行调整。
贝叶斯岭回归
自动关联判定-ARD
高维数据的线性回归
特征选择
在实际应用中,特征数量往往非常多,其中即包含了我们需要的与目标相关的特征,也有一些完全不相关的特征,并且特征之间也可能存在相互依赖。这会导致对应的模型就越复杂,模型训练和预测需要的计算量就越大,同时也会影响算法的预测能力。
特征选取就是从大量的特征中选取一个特征子集,构造出更好的模型(如残差最小)。
特征选择分为产生、评估、验证三大步骤,如下图。

特征选择的过程 ( M. Dash and H. Liu 1997 )
1. 特征生成
特征产生过程是搜索特征子空间的过程。分为一下3大类
- 完全搜索
完全搜索又分为穷举搜索(Exhaustive)和非穷举(Non-Exhaustive)两类。
- 广度优先搜索
- 分支界限搜索
- 定向搜索
- 最优有限搜索
- 启发式搜索
- 序列前向选择
- 序列后向选择
- 双向搜索
- 增L去R选择算法
- 序列浮动选择
- 决策树
- 随机搜索
- 随机产生序列选择算法
- 模拟退火算法
- 遗传算法
2. 特征评估
评价函数
- 相关性
- 距离
- 信息增益
- 一致性
- 分类器错误率
3. 特征验证
最小角回归(Least-angle Regression, LARS)
针对高位数据,最小角回归LARS算法首先是一种逐步向前回归。在逐步向前的每一步中,它都会找到与目标最相关的特征。当特征具有相等的相关性时,它不是沿着相同的特征继续进行,而是沿着特征之间等角的方向进行。
参考LeastAngle_2002.pdf了解更多最小角回归算法的更多细节。
LARS Lasso
LarsLasso是利用LARS算法实现的LASSO模型,与基于坐标下降的LASSO模型不同,它得到的是分段线性的精确解,是其自身系数范数的函数。

正交匹配追踪(OMP)
一种类似于最小角回归的前向特征选择方法,正交匹配追踪可以用固定数目的非零元素逼近最优解向量。或者,正交匹配追踪可以针对特定的误差,而不是特定数目的非零系数。
参考 KSVD-OMP-v2.pdf。
随机梯度下降(SGD)
随机梯度下降是一种简单而又非常有效的拟合线性模型的方法。当样本数量(和特性数量)非常大时,它特别有用。
感知机 (Perceptron)
Perceptron 是另一种适用于大规模学习的简单分类算法。有如下默认:
- 它不需要设置学习率
- 它不需要正则项
- 它只用错误样本更新模型
最后一个特点意味着Perceptron的训练速度略快于带有合页损失(hinge loss)的SGD,因此得到的模型更稀疏。
被动感知算法(Passive Aggressive Algorithms)
被动感知算法是一种大规模学习的算法。和感知机相似,因为它们不需要设置学习率。然而,与感知器不同的是,它们包含正则化参数 C 。
广义线性回归(GLM)
广义线性模型(GLM)以两种方式扩展了线性模型。
- 反向连接函数
首先是预测值 y ^ \hat y y^是否通过反向连接函数 h h h连接到输入变量 X X X的线性组合。
y ^ ( w , X ) = h ( X w ) \hat y(w, X) = h(Xw) y^(w,X)=h(Xw)
- 损失函数
其次,平方损失函数被一个指数分布的单位偏差 d d d所代替 (更准确地说,一个再生指数离散模型(EDM) )。最小化问题变成
min w 1 2 n s a m p l e s ∑ i d ( y i , y i ^ ) + α 2 ∥ w ∥ 2 \min_w \frac{1}{2n_{samples}} \sum_i d(y_i, \hat{y_i}) + \frac{\alpha}{2}\|w\|_2 minw2nsamples1∑id(yi,yi^)+2α∥w∥2
α \alpha α是L2正则化惩罚项。提供样本权重后,平均值即为加权平均值。
再生指数离散模型(EDM)

TweedieRegressor
TweedieRegressor为Tweedie分布实现了一个广义线性模型,该模型允许使用适当的 p o w e r power power参数对上述任何分布进行建模。
- power = 0: 正态分布。在这种情况下,诸如 Ridge, ElasticNet 等特定的估计器通常更合适。
- power = 1: 泊松分布。方便起见可以使用 PoissonRegressor 。然而,它完全等同于 TweedieRegressor(power=1, link=‘log’).
- power = 2: 伽马分布。方便起见可以使用GammaRegressor 。然而,它完全等同于 TweedieRegressor(power=2, link=‘log’).
- power = 3: 逆高斯分布。
分配方式选择
分配方式的选择取决于手头的问题:
- 如果目标值 是计数(非负整数值)或相对频率(非负),则可以使用带有log-link的泊松偏差。
- 如果目标值是正的,并且是歪斜的,您可以尝试带有log-link的Gamma偏差。
- 如果目标值似乎比伽马分布的尾部更重,那么您可以尝试使用逆高斯偏差(或者更高的Tweedie族方差)。
参考
- 【SVR回归分析简明教程】https://zhuanlan.zhihu.com/p/33692660
- 【scikit-learn支持向量机/回归】http://scikit-learn.org.cn/view/83.html#
- 【SVR支持向量回归】https://scikit-learn.org.cn/view/782.html
- 【使用线性与非线性核的支持向量机回归】http://scikit-learn.org.cn/view/342.html
- 【统计学——回归分析】https://zhuanlan.zhihu.com/p/352694434
- 【从入门到放弃——线性回归】https://zhuanlan.zhihu.com/p/147297924
- 【回归模型偏差、方差和残差】https://zhuanlan.zhihu.com/p/50214504
- 【马氏距离】https://zhuanlan.zhihu.com/p/46626607
- 【Lasso回归和Ridge回归的区别】https://cloud.tencent.com/developer/article/1556213
- 【深入理解L1、L2正则化】https://www.cnblogs.com/zingp/p/10375691.html#_label0
- 【机器学习中正则化项L1和L2的直观理解】https://blog.csdn.net/jinping_shi/article/details/52433975