吴恩达深度学习笔记
你将学习本系列课程(专业):
- 神经网络和深度学习
- 改进深度神经网络:超参数调优、正则化和优化
- 构建你的机器学习项目吨/德
- 卷积神经网络端到端
- 自然语言处理:建立序列模型RNN,LSTM
我的目标
理解深度学习基本原理 常用算法 流程 常用术语 不求算术推导 不求算术推导 不求算术推导 使用深度学习框架
入门介绍
例1 房价预测模型
输入映射输出
监督学习有价值的
图像卷积序列 CNN
时间序列 语言序列 RNN RNNS
深度学习神经网络
数据量和质量处于第一序列胜过算法
算法主要加速学习速率如
sigmod 函数转化为ReLU 函数 梯度下降更快
规模推动深度学习进步 1数据2算力3算法
所以 算法 只是第三重要的
课程安排
本课程大纲第一周:介绍
第2周:神经网络编程基础
第3周:一个隐层神经网络
第4周:深度神经网络
算法 logisttic 回归 解决二二分类 (二元分类)
最小的神经网络
二元分类(二分类): 输入特征向量 输出 0 or 1
例2:有猫吗预测
训练集合样本
t r a i n g = { ( x 1 , y 1 ) , ( . ) . . . . . . } traing = \{(x^1,y^1),(.)......\} traing={(x1,y1),(.)......}
$$
测试集合样本
logisttic 回归 函数 sigmoid 是一个方程 S形的
$$
y — = ( w T + B ) z 0 < = y < 01 y^{—} = \frac{(w^T+B)}{z} 0<=y<01 y—=z(wT+B)0<=y<01

w 和 b 是 参 数 我 们 通 常 将 其 分 开 作 为 一 个 向 量 参 数 w 和b是参数 我们通常将其分开作为一个向量参数 w和b是参数我们通常将其分开作为一个向量参数
Θ = [ b w 0 w 1 w 2 . . . ] \Theta = \left[\begin{array}{c} b \\w_0\\w_1\\w_2\\... \end{array} \right] Θ=⎣⎢⎢⎢⎢⎡bw0w1w2...⎦⎥⎥⎥⎥⎤
y ^ 预 测 值 对 应 的 是 训 练 样 本 的 输 出 \hat{y} 预测值对应的是训练样本的输出 y^预测值对应的是训练样本的输出
logisttic 的成本函数 回归损失函数
损失函数
衡量了单个个训练样本上的表现
效果近似于方差但后面更好维护
δ ( y ^ , y ) = − ( y l o g ( ^ y ) + ( 1 − y ) l o g ( 1 − y ^ ) ) 近 似 于 1 2 ( y ^ − y ) 2 样 本 值 y ^ 真 实 值 y \delta(\hat{y},y) = -(ylog\hat(y)+(1-y)log(1-\hat{y})) 近似于 \frac{1}{2}(\hat{y}-y)^2 样本值\hat{y} 真实值y δ(y^,y)=−(ylog(^y)+(1−y)log(1−y^))近似于21(y^−y)2样本值y^真实值y
成本函数
衡量了全体训练样本上的表现
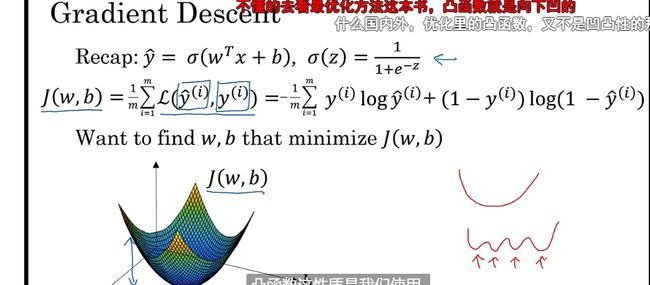
J ( w , b ) = − 1 2 ∑ i = 1 m y i l o g y ^ i + ( 1 − y ^ ) J(w,b) = -\frac{1}{2}\sum^{m}_{i=1}y^ilog\hat{y}^i+(1-\hat{y}) J(w,b)=−21i=1∑myilogy^i+(1−y^)
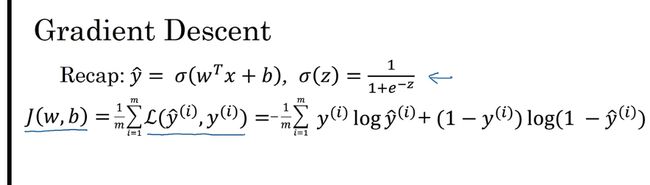
梯度下降法
找到凸函数的最低点 即最优解
学习率a
导数即函数的斜率即高除宽
J 成本函数
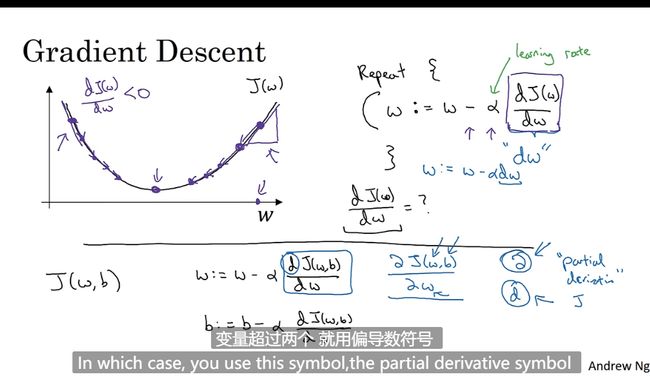
w : = w − α d J ( w ) d w w := w-\alpha\frac{dJ(w)}{dw} w:=w−αdwdJ(w)
反向传播 backpagagations
反向传播就是求导
导数
导数大多时候就是斜率 即高除宽
d d a f ( a ) \frac{d}{da}f(a) dadf(a)
导数例子
导数时刻变得
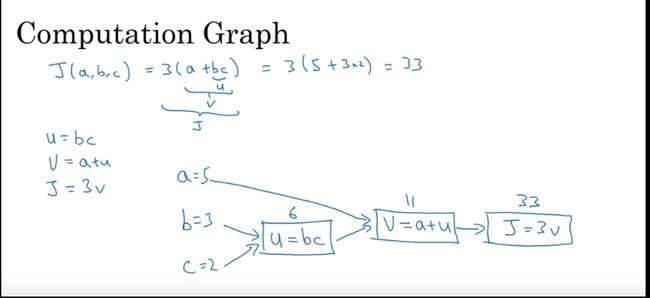
计算图
流程图从左到右
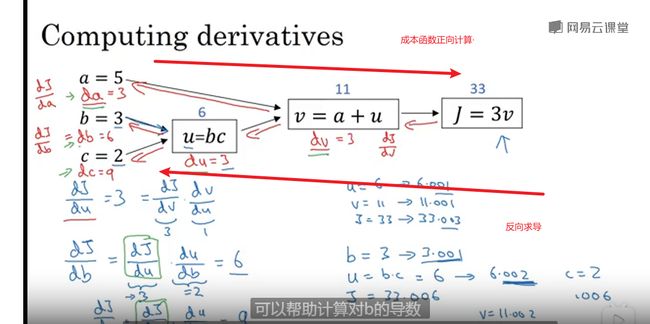
计算图求导
反向求导
链式法则
dvar 表示导数
logistic (逻辑)回归中的梯度下降法
计算偏导数,导数流程图计
算梯度
logistic 回归公式
z = w T x + b 单 个 样 本 成 本 函 数 y ^ = a = δ ( z ) 成 本 函 数 L ( a , y ) = − ( y l o g ( a ) + ( 1 − y ) l o g ( 1 − a ) ) 损 失 函 数 z = w^Tx+b 单个样本 成本函数 \\ \hat{y}=a=\delta(z) 成本函数 \\ L(a,y)=-(ylog(a)+(1-y)log(1-a)) 损失函数 z=wTx+b单个样本成本函数y^=a=δ(z)成本函数L(a,y)=−(ylog(a)+(1−y)log(1−a))损失函数
dz =a-y
梯度更新过程
m个样本的梯度下降
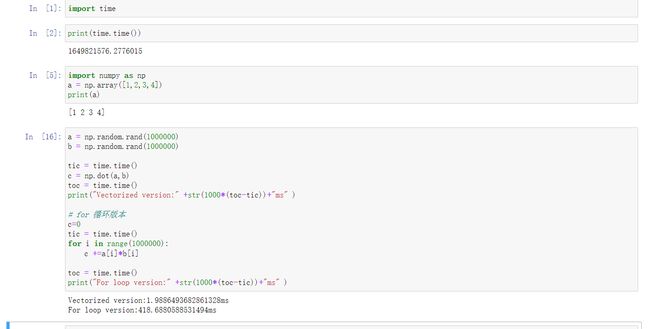
向量化
摆脱for 循环的低效率 加速运算
向量计算会比for 循环快300 倍
用numpy 就是np
是在做并行计算
原因SIMD 单指令流多数据流 single instruct mult data
其他向量化例子
这里指的就是numpy 的其他函数
np.log
np.abs
np.max
np.exp。。。。。。
np.zeros(n-x,1)
向量化logistic 回归的梯度输出
将数据集也向量化
db = 1/m *np.sum(dz)
python 中的广播
术语广播描述了NumPy在算术运算期间如何处理具有不同形状的数组。受某些限制,较小的阵列在较大的阵列中“广播”,以便它们具有兼容的形状。广播提供了一种将数组操作矢量化的方法,这样循环就可以在C语言而不是Python语言中发生。这样做时不会产生不必要的数据拷贝,通常会导致高效的算法实现。然而,在某些情况下,广播是一个坏主意,因为它会导致内存使用效率低下,从而降低计算速度。
NumPy操作通常是在逐元素的基础上对数组进行的。在最简单的情况下,两个数组必须具有完全相同的形状,如下例所示:
broadcasting
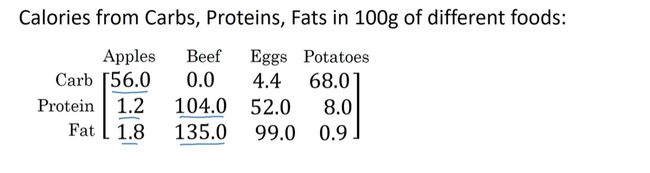
卡路里计算
A = np.array([[56,0,4.4,68],[1.2,104,52,8],[1.8,135,99,0.9]])
print(A)
cal = A.sum(axis=0)# 竖直方向
cal_ = A.sum(axis=1)# 横向
print(cal)
percentage = 100*A/(cal.reshape(1,4))
print(percentage)
python_numpy 向量说明
减少BUG 减少一维的向量
Jupyter_ipython 指南
略
logistic 损失函数
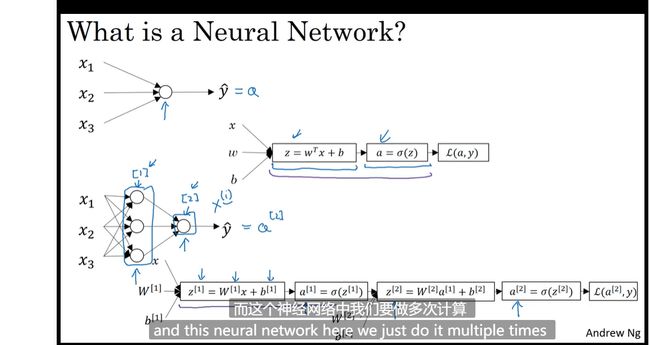
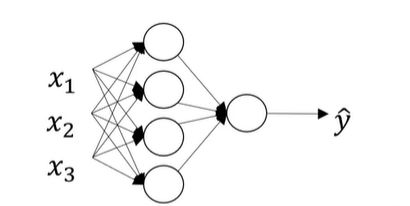
神经网络概述
多层级结构
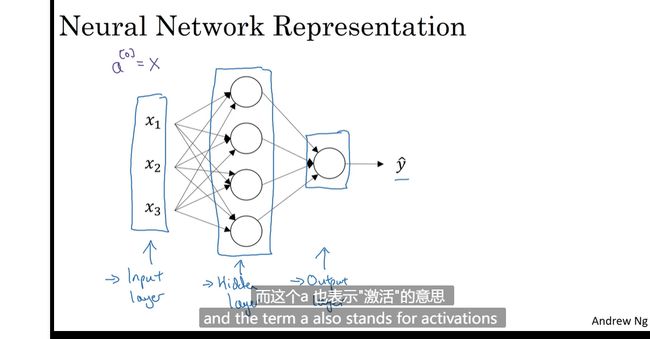
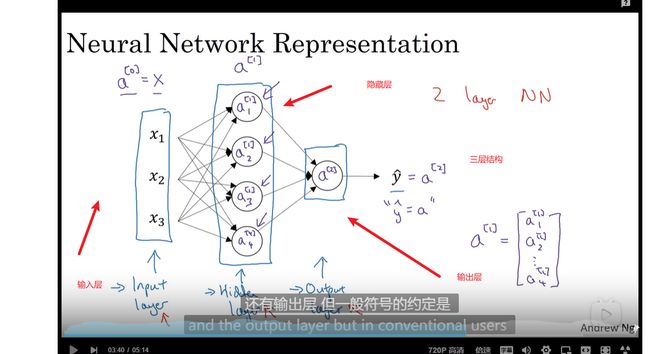
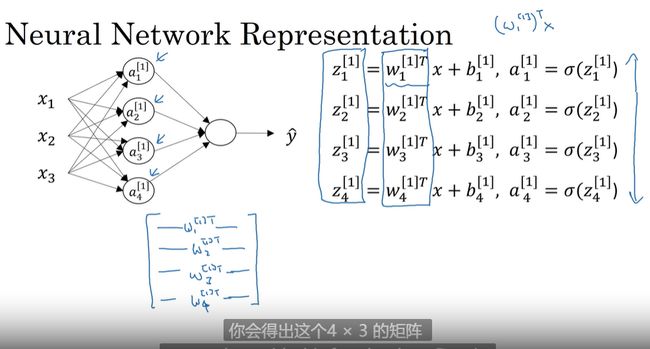
神将网络表示
输入层为第零层 有时候也不考虑进去
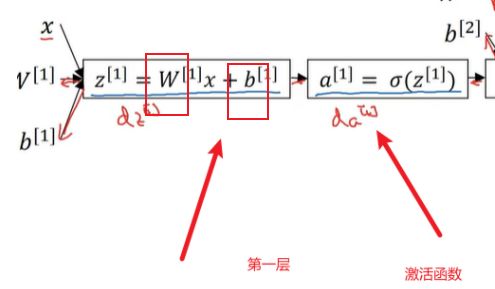
计算神经网络的输出
层数和节点数
神经网络的每一个隐层有多个节点的输出看作logistic 的输入到下一层
多个样本的向量化–模拟神经网络
激活函数:节点函数
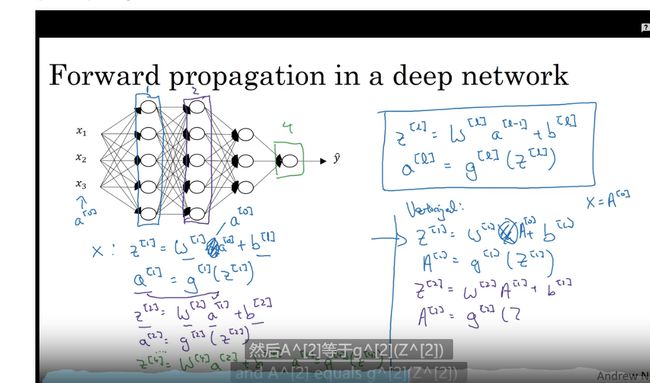
z [ 1 ] = W [ 1 ] X + B [ 1 ] a [ 1 ] = σ ( z 1 ) z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ] a [ 2 ] = σ ( z [ 2 ] ) z^{[1]}=W^{[1]}X+B^{[1]}\\ a^{[1]}=\sigma(z^{1})\\ z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}\\ a^{[2]}=\sigma(z^{[2]}) z[1]=W[1]X+B[1]a[1]=σ(z1)z[2]=W[2]a[1]+b[2]a[2]=σ(z[2])
向量化实现的解释
数据转化向量
激活函数
神经网络中处理上一层输出转化为下一层输入的函数
σ 函 数 输 出 层 使 用 因 为 介 于 0 − 1 \sigma 函数 输出层使用 因为介于0-1 σ函数输出层使用因为介于0−1
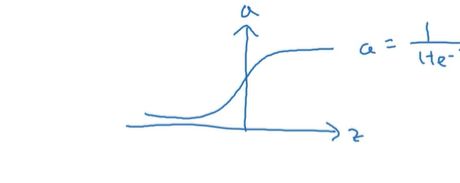
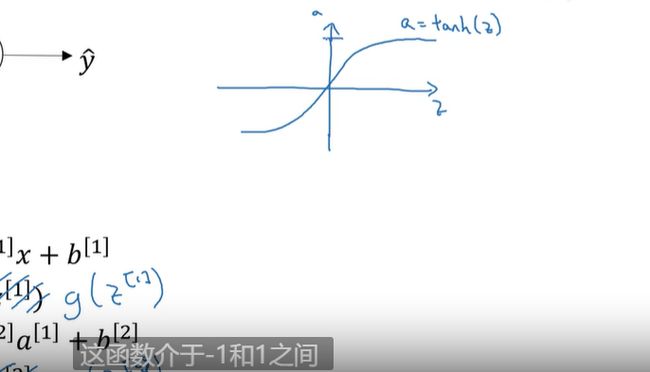
tanh 函数效果更好
$$
$$
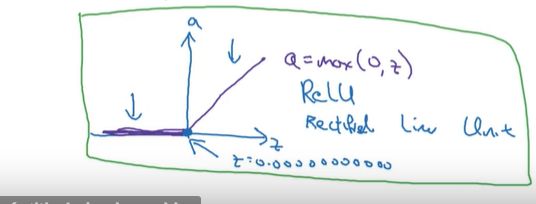
ReLU函数 和带泄露(leaky)的ReLU函数
$$
激活函数为了是梯度快速下降
斜率越小梯度下降越慢
为什么要用非线性激活函数
为什么不把输出值直接输出要使用激活函数处理?
若使用恒等激活函数,或者线性激活函数,隐藏层会失效不如去掉神经网络无法成立–事实证明?
只有机器学习的回归问题可以使用线性方程如房价预测输出的是一个实数,隐藏层就是不能用线性
激活函数的导数
激活函数求导过程 略
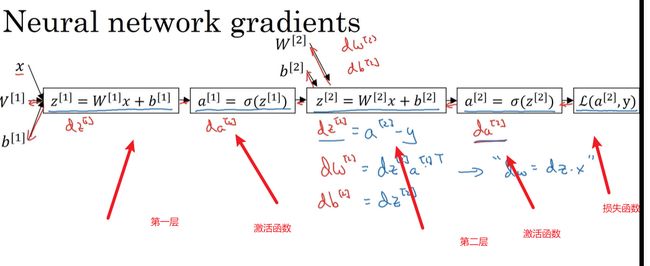
神经网络的梯度下降法
训练模型随机初始化参数很重要
梯度下降更新 步伐根据学习率
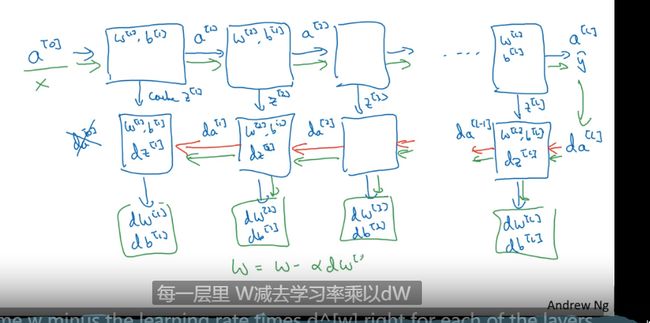
直观理解反向传播
**前向传播(Forward Propagation)**前向传播就是从input,经过一层层的layer,不断计算每一层的z和a,最后得到输出y^ 的过程,计算出了y^,就可以根据它和真实值y的差别来计算损失(loss)。
**反向传播(Backward Propagation)**反向传播就是根据损失函数L(y^,y)来反方向地计算每一层的z、a、w、b的偏导数(梯度),从而更新参数
正向传播 反向传播(求导)
随机初始化
参数w 偏置项b
w 不要是0会使节点单元变得一样 b可以
W 不宜太大可能一开始就饱和
减慢学习效率 0.01 左右是合理的
深层网络中的前向传播
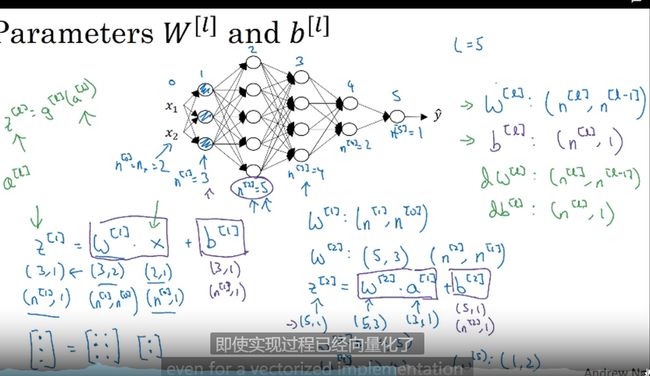
核对矩阵的维数
搭建深层神经网络块
参数& 超参数
超参数:控制参数的参数
如学习率 a 循环的数量 隐层的数量等控制 W和b 的参数 还有momentum ,batch size等
调参很多就是调超参数
和大脑的关系
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5VntkwF9-1651913336000)(C:\Users\renoy\AppData\Roaming\Typora\typora-user-images\image-20220414152711834.png)]、
一个类比蹭热度用的,也许有收到一些生物学的启发吧
一些大佬经验讲解分享
ReLU向后传播
训练__开发__测试集
训练集 验证集(开发集合) 测试集
验证集一般用于进一步确定模型中的超参数(例如正则项系数、神经网络中隐层的节点个数,k值等),而测试集只是用于评估模型的精确度(即泛化能力)。
传统6 -2 -2 ,8 -1 -1
大数据(百万级别)
98 - 1 -1
测试集 也可以 并入验证集 就没有无偏评估集合了
偏差_方差
高偏差
拟合的数据不会是线性的
机器学习基础
计算偏差 太高训练集都不行的话 换一个网络架构训练
高偏差和高方差是完全不同的情况。解决方法也不一样
**偏差:**描述的是预测值(估计值)的期望与真实值之间的差距。偏差越大,越偏离真实数据,如下图第二行所示。
**方差:**描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散,如下图右列所示。
正则化–降低方差
正则化是为了降低方差
过度拟合了数据即存在高方差问题
解决方案
1 正则化
2 准备更多训练数据
L2 范数正则化也被称为“权重衰减”
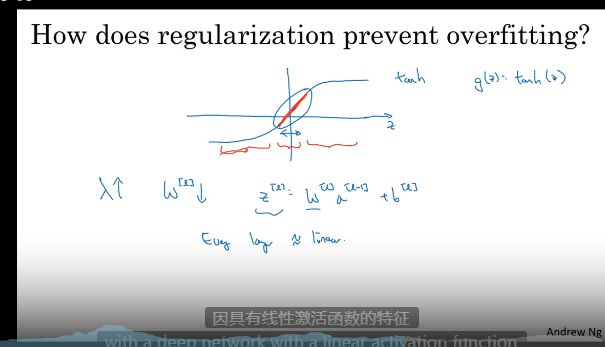
为什么正则化可以减少过拟合
经验后的结果–惩罚函数
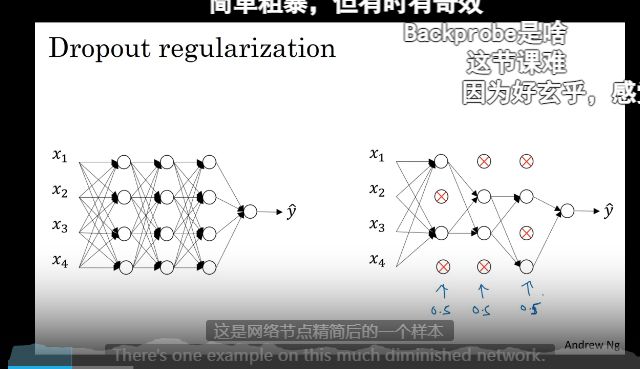
Dropount 正则化
随机失活
消除一些节点?
理解dropout
不太理解
其他正则化方法
1 数据扩增----造数据
2 early stopping
提早停止训练
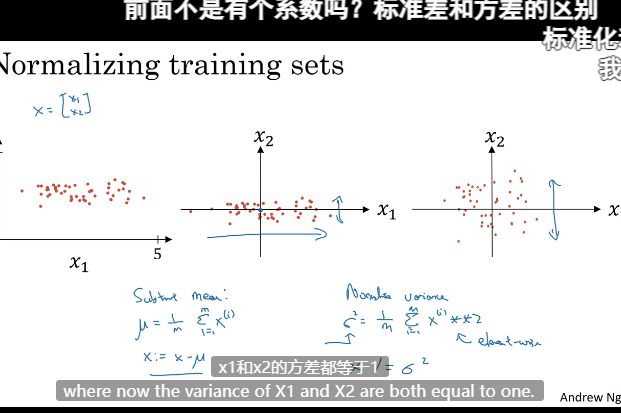
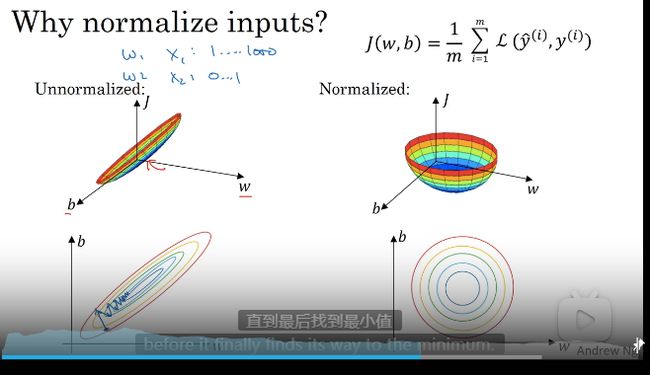
归一化(标准化)输入–加速训练
加速训练的方法,优化代价函数J
归一化前后对比
前者学习率很低
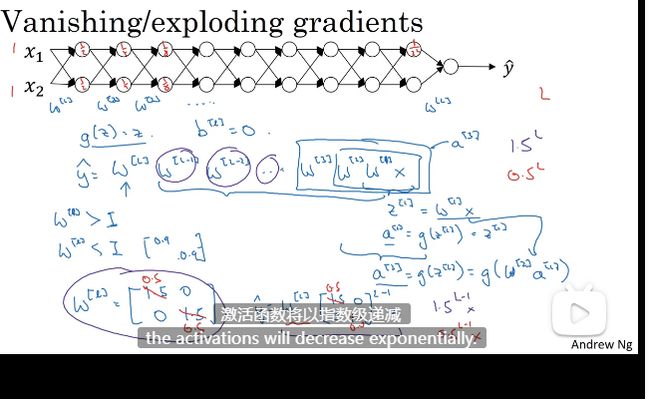
梯度消失与梯度爆炸
需要更聪明的随机初始化权重
W 激活函数
W 比1 的结果是指数爆炸增大
W 比1 小一点的结果是指数递减
神经网络的权重初始化
解决但不能完全解决梯度消失与梯度爆炸
梯度的数值逼近
双边误差不使用单边公差
梯度检验
向量化 W 矩阵
执行循环 计算双边误差
計算兩個向量的距离 欧式距离,他是误差平方之和
不明白哦
关于梯度检验实现的标记
Mini-batch梯度下降算法
不用等整个数据集处理完再执行下一步
Mini-batch梯度下降算法就是在分割数据的同时分批次执行梯度下降
深度学习高度依赖经验
算法优化
条件一 向量化计算
当数据很大是 流程如下 处理500w 数据进入下一层 处理500w 数据进入下一层 就会很慢
需要梯度下降法处理一部分
处理思路分割数据集 这些子集被称之为Mini-batch 如一次1000 个数据 一组一组进去 ,有5000 组
需要遍历数据集了 ,遍历还是少不了的
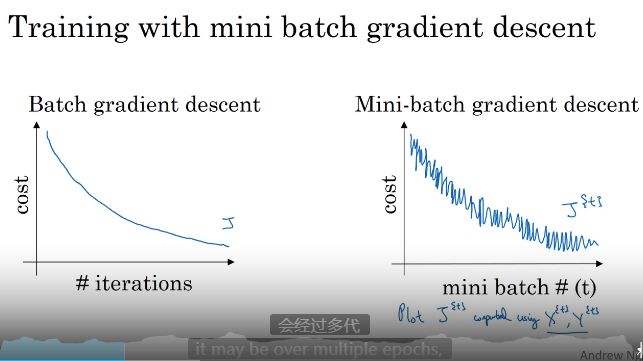
理解mini-batch size梯度下降
遍历让每次迭代的成本降低了
每次迭代都是训练不同数据
每次计算成本下降
举个例子
随机梯度下降 size = 1 随机梯度下降 等于一个接着一个计算没有向量计算了 low
梯度下降 size = m 全部向量化 数据多了顶不住 low
所以选择size 很重要
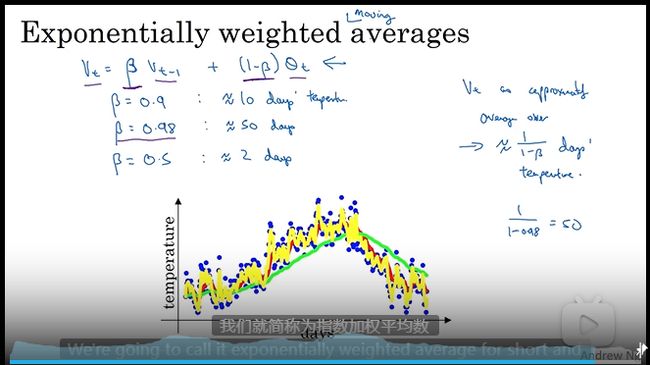
指数加权平均(指数加权移动平均)
比梯度下降快的算法需要用到
调整贝塔 参数 调参数调参数
理解指数加权平均
用之前数据对之后的数据影响有多大
指数加权平均的偏差修正
一些算法
为了加速训练
局部最优的问题
导数接近0下降很慢了
调试处理
超参数选择–玄学
为超参数选择合适的范围
随机均匀取值
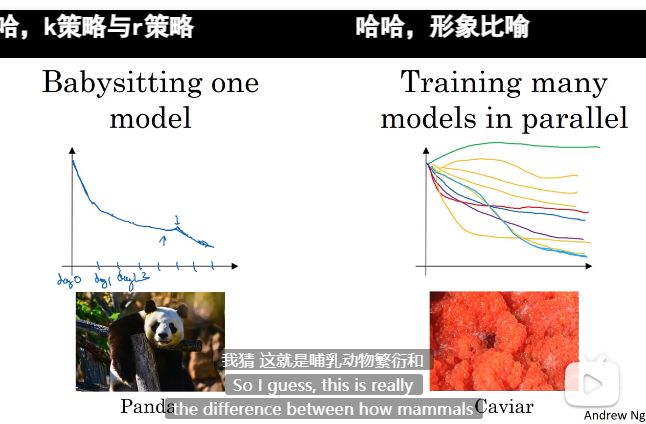
超参数训练的实践:Pandas VS Caviar
超参数调整 可能是一直要调整的
两种策略 1 不停迭代一个模型持续优化 2 大量模型一起训练 的最优的
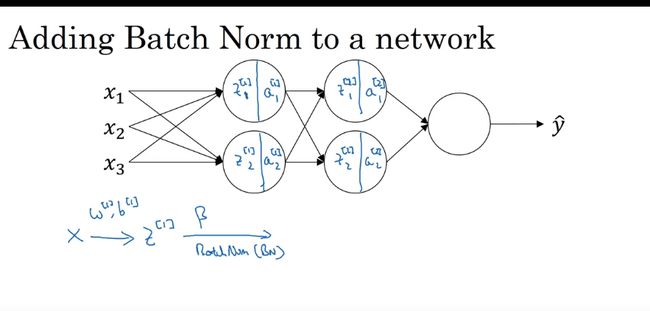
正则化网络的激活函数
将Batch Norm (Batch 归一化)拟合进神经网络
加速学习
拟合就是把平面上一系列的点,用一条光滑的曲线连接起来。因为这条曲线有无数种可能,从而有各种拟合方法。
Bath Norm 为什么奏效
测试时的Batch Norm
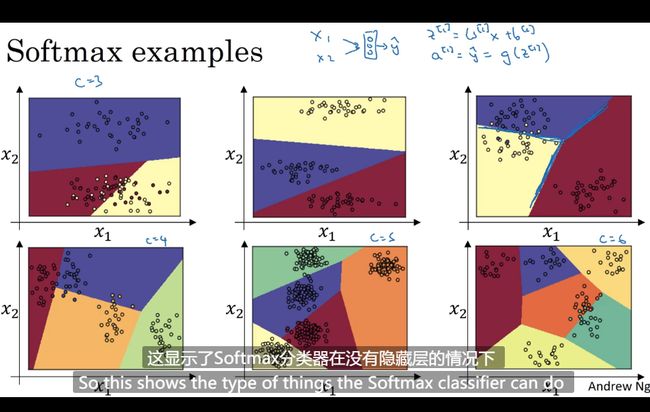
Softmax 回归
分类器 用来决定边界
训练一个Softmax 分类器
对应的是 hardmax 即输出的是一个概率
深度学习框架
专注于正向传播框架计算反向传播
数据参数是对的其他自动了
TensorFlow
只需要清楚的正向传播流程
框架实现反向传播和梯度计算
import numpy as np
import tensorflow as tf
w = tf.Variable # w 我们要优化的参数 tensor 变量
coefficients = np.array([[1.],[-10.][25.]])
x = tf.placeholder(tf.float32,[3,1]) # 定义 引入参数x 稍后把把常量放入
# cost = tf.add(tf.add(w**2,tf.multiply(-10,w)),25) # 定义损失函数
# cost = w**2 - 10*w +25 # 定义损失函数 (w-5)**2
cost = x[0][0]*w**2 +x[1][0]*w +x[2][0] # 定义损失函数
train = tf.train.GradientDescentOptimizer(0,0.01).minimize(cost)
init = tf.global_variables_initializer()
session = tf.Session() # with tf.Session() as session
session.run(init)
print(session.run(w)) # 什么都没做 -->0
session.run(train) # 运行下一步的梯度下降法
print(session.run(w)) # -->0.1
迭代1000次
for i in range(1000):
session.run(train,feed_dict={x:coefficients})
# 把不同的mini_batch 放入 损失函数需要的地方
print(session.run(w)) # -->4.99999
访谈大佬二
1 研究方向有无监督 产品化有监督 六个月入行没问题 计算机和数学的知识 概率代数最优化微积分
2 PaddlePaddle 之类的平台提供资源
为什么是 ML策略
当准确率不够了 1 更多的数据 2 数据的多样性 3 训练的再久一点 4 算法更新 5网络更新
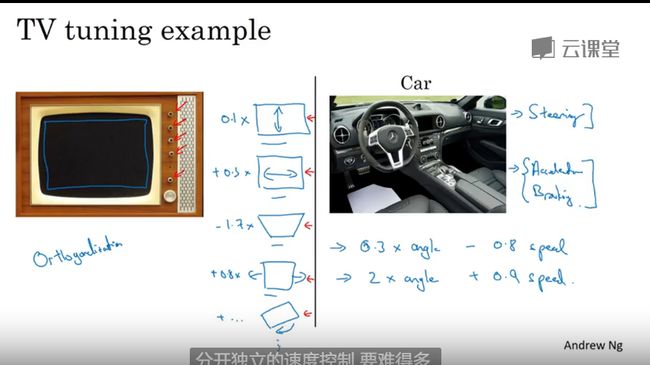
正交化
每个维度负责一个方向
超参数解耦
1 先到能接受的程度
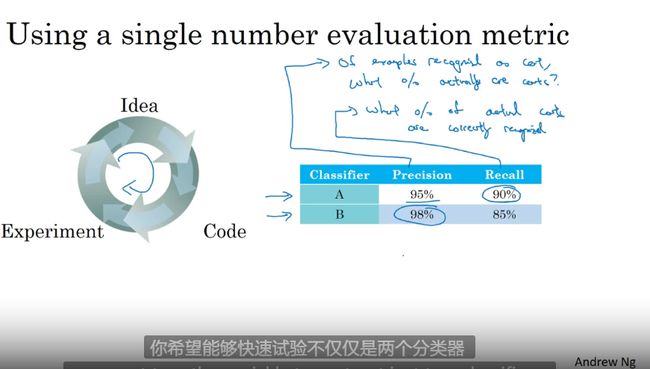
单一数字评估指标
参数分类指标可视化
满足和优化指标
训练 - 开发- 测试集划分
设立开发集和目标
开发集合测试集的大小
没有单独的测试集合也可以
测试集合和开发集合合并为开发集合(数据大的时候)
什么时候该改变开发-测试集和指标
业务 错误率
分类器
为什么是人的表现
根据用户实际情况修改数据
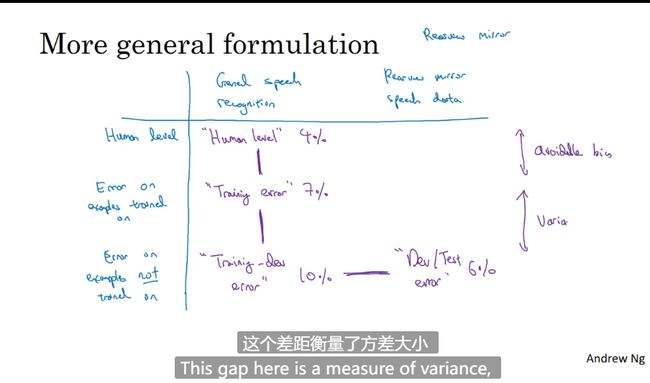
可避免偏差
理解人的表现
贝叶斯错误替代
超过人的表现
改善模型的表现
进行误差分析
消除标注错误的数据
先看错误率
快速搭建你的第一个系统,并进行迭代
在不同的划分上进行训练并测试
语音识别
不匹配数据划分的偏差和方差
数据不匹配 开发集错误
解决数据不匹配
数据增强 造数据
迁移学习
不同场景可以复用 串行学习?
预训练和微调学习来源的权重
从一个任务中学习,然后迁移到不同任务中去
多任务学习
多个任务中并行学习而不是串行
多任务学习不同任务的数据量要对等
区别 迁移学习:一次解决 多个任务而不是试图用A 的解决B
迁移学习使用频率更高一些
场景 有一个好的网络 少量的数据 现在可以使用迁移学习了,迭代训练
什么是端到端的深度学习
忽略所有中间阶段 一个神经网络代替它
例子1 语音识别 x --> y
传统的 x --> 特征提取 --> 算法找音位(基本单位)—> 中间件 一步一步 找到 y
端到端
x -> y
大数据使用端到端效果 比传统还好
例子2 人脸识别门禁
输入的数据其实是多步的 1 检测器找人脸位置 2 放大人脸剪裁到居中位置
这个例子中 没有使用端到端 因为 拆分之后获取数据,训练更简单 ,如果可以拆成多个简单的任务效果也会比端到端好
总结来说没有足够的数据来支撑端到端就使用分阶段解决的方式
是否要用端到端的深度学习
1 好处是只要数据 不要过程
2 坏处是没有过程
还是分步的更有前景因为端到端的数据太难收集了
大佬访问3
1 机器学习是人工智能的优雅实现 输入数据代码自动修正 深度学习 监督学习效果真好 —知道底层不要随便抽象化。从0开始实现一遍不要一开始就用Tensorflow
2 算力提升 推动了 预训练到标准反向传播的转变
计算机视觉
目标检测
风格迁移
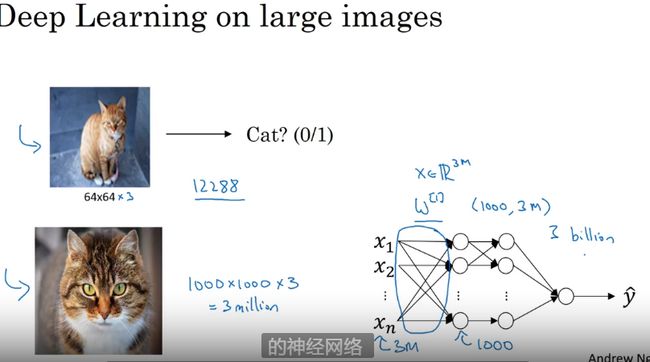
图片 数据量【x*y*3】 3 个通道
卷积运算使得处理图片不需要如此巨大的内存
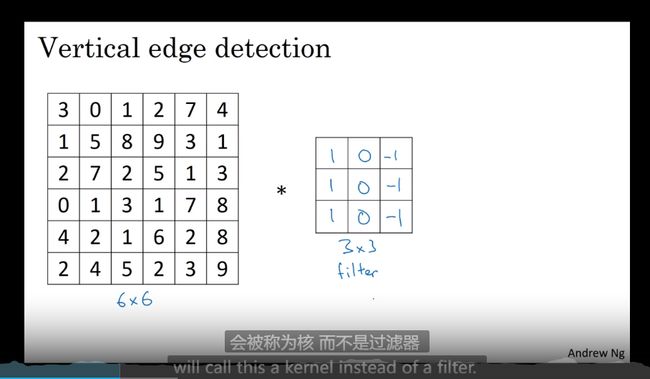
边缘检测实例—卷积运算
检测边缘 -> 局部-> 整体
过滤器 卷积核
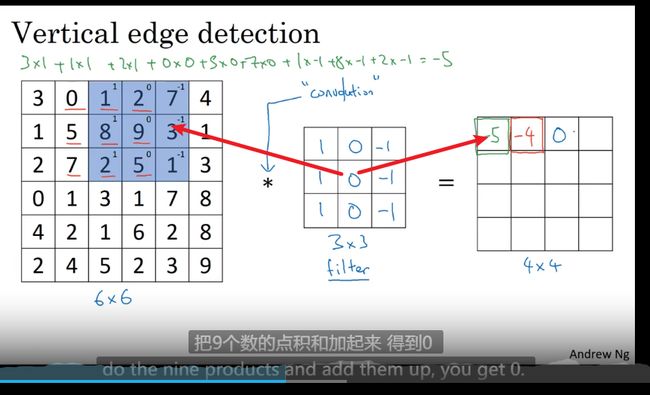
每个对应位置相乘加起来
过滤器(卷积核)在 原图上计算 得到新的结果 使原图变小
Keras
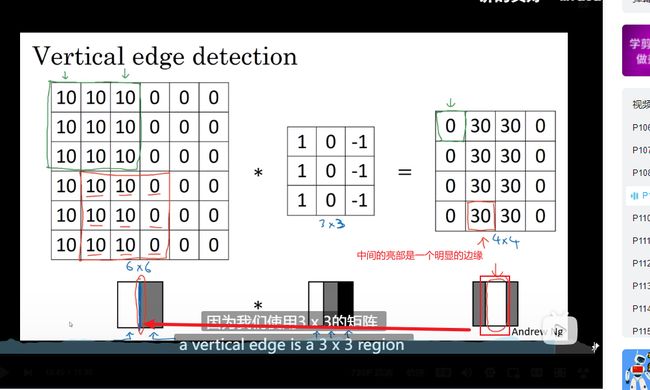
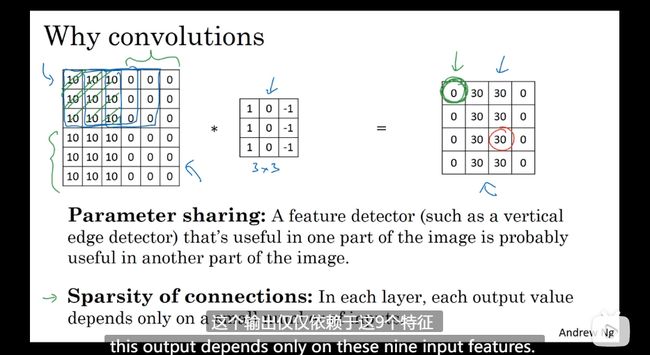
为什么卷积可以做垂直边缘检测
垂直边缘检测
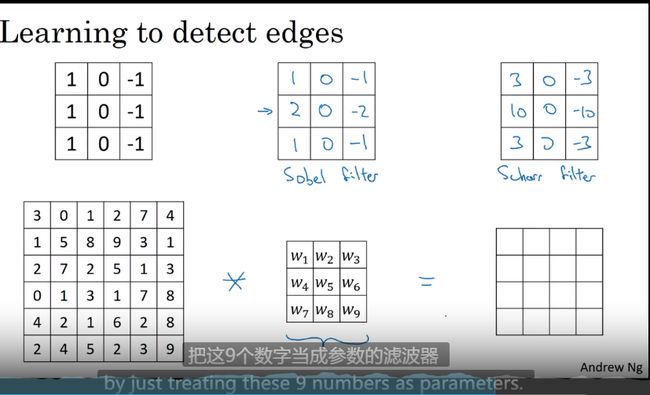
更多边缘检测内容
水平边缘检测
![]()
各种滤波器
九个数字当成参数 自定义各种滤波器
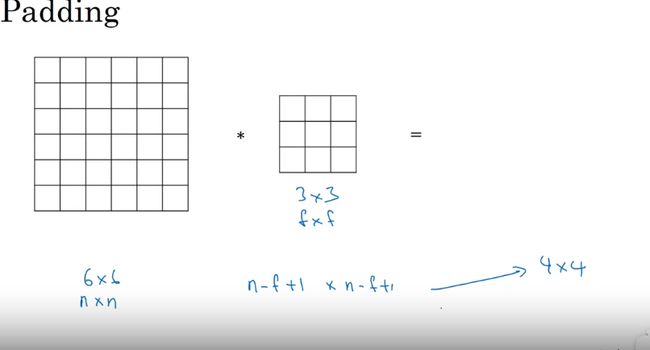
Padding (填充)-- 一个基本卷积操作
卷积生成公式
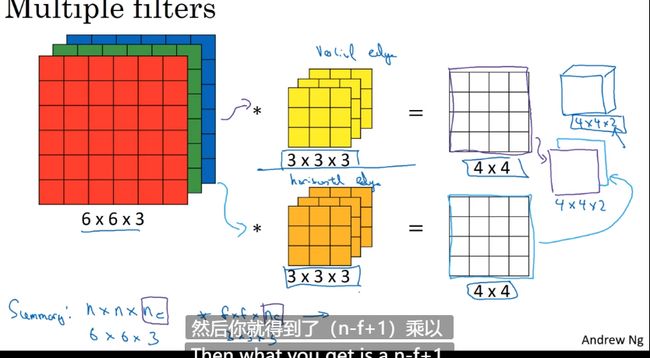
n ∗ n 卷 f ∗ f ( 过 滤 器 ) = n − f + 1 ∗ n − f + 1 6 ∗ 6 ∗ 3 ∗ 3 = 4 ∗ 4 n*n 卷 f*f(过滤器) = n-f+1 * n-f+1 \\ 6*6 * 3*3 = 4*4 n∗n卷f∗f(过滤器)=n−f+1∗n−f+16∗6∗3∗3=4∗4
卷积的缺点
1 输出缩小:图片多次卷积之后会不断缩小最终 1*1
2 信息丢失:最边缘的像素 只被一次使用 (一些图片处理中会造成毛边)
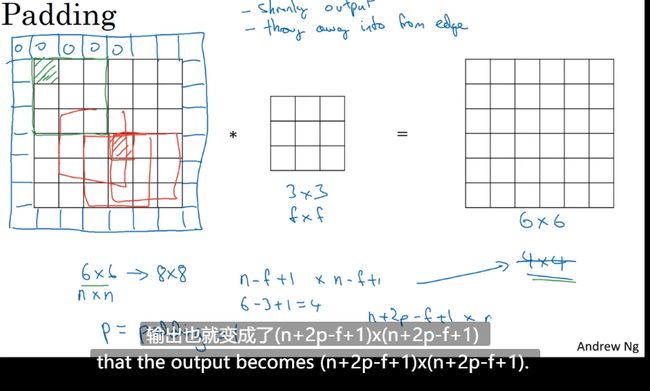
Padding(填充)解决这两个问题
在图像边缘填充一层像素
n + 2 p − f + 1 ∗ n + 2 p − f + 1 填 充 之 后 的 n+2p-f+1 * n+2p-f+1 填充之后的 n+2p−f+1∗n+2p−f+1填充之后的
Valid(不填充) 和 Same(相同) convolution(卷积)
为了保障 输出后的图片等于原图
n + 2 p − f + 1 = n − − > p = f − 1 2 n+2p-f+1 = n --> p = \frac{f-1}{2} n+2p−f+1=n−−>p=2f−1
f 大都是奇数 原因
1 偶数只能填充不对称了
2 奇数 的卷积核会有一个中点像素,相邻关系更好计算
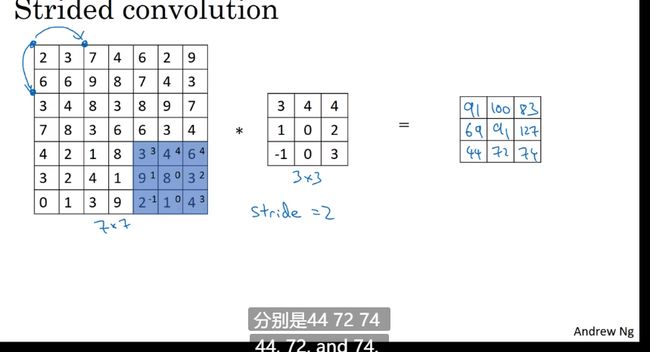
卷积步长
当步长为二
商不是整数向下取整,原因是过滤器移动到超出原图的位置就不要操作了
地板除 [z] = floor(z)
[ n + 2 p − f s + 1 ] ∗ [ n + 2 p − f s + 1 ] 卷 积 结 果 [\frac{n+2p-f}{s} +1] * [\frac{n+2p-f}{s} +1] 卷积结果 [sn+2p−f+1]∗[sn+2p−f+1]卷积结果
卷积的结果需要镜像&反转
互相关(卷积) 反转可以省略
三维卷积
三维计算
立体卷积真的很有用
单层卷积网络
过滤器 填充层 步幅
简单卷积网络实力
![外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-70xrhggj-1651913336015)(C:\Users\renoy\AppData\Roaming\Typora\typora-user-images\image-20220428172829147.png)]
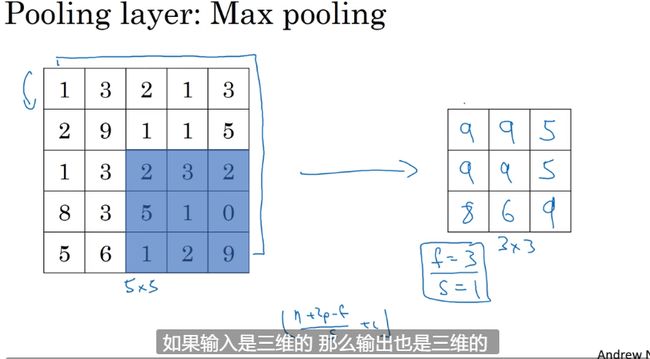
池化层
保留特征输出
卷积层和池化层区别
卷积层
功能 提取特征
操作 对于三维数据比如RGB图像(3通道),卷积核的深度必须同输入的通道数,输出的通道数等于卷积核的个数。卷积操作会改变输入特征图的通道数。
特性 权值共享:减少了参数的数量,并利用了图像目标的平移不变性。稀疏连接:输出的每个值只依赖于输入的部分值。
池化层
功能 压缩特征图,提取主要特征
操作 池化只是在二维数据上操作的,因此不改变输入的通道数。对于多通道的输入,这一点和卷积区别很大。
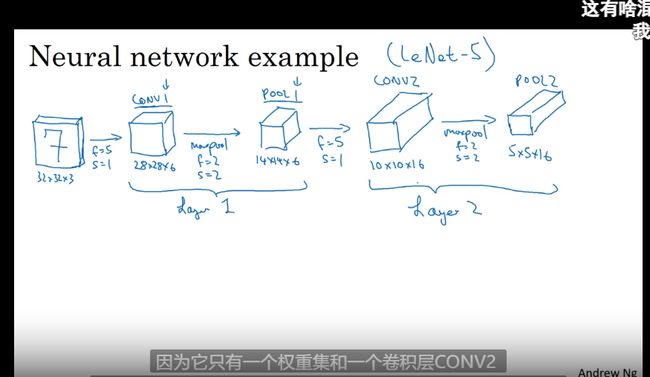
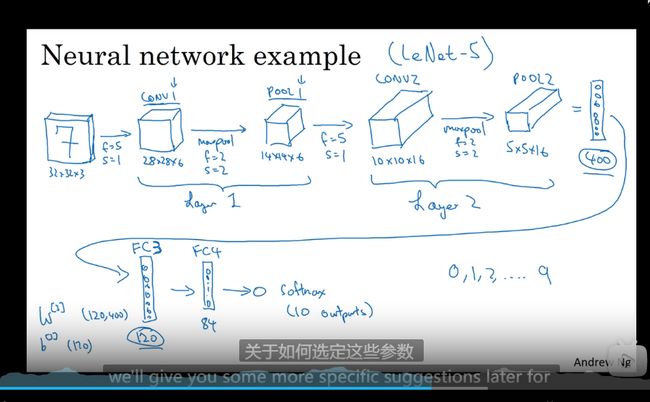
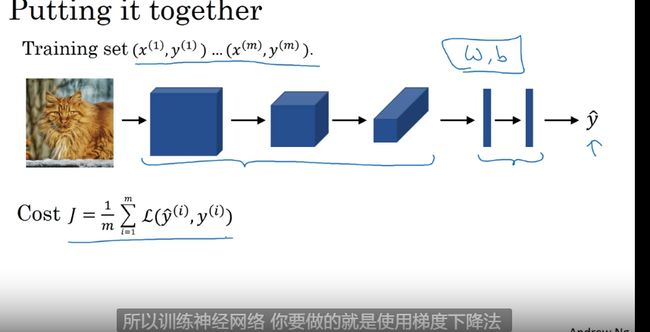
全链接卷积神经网络事例
这里一个卷基层包含一个卷基层和一个池化层
Conv1 + POOL1 作为Layer1
尽量不要自己设置超参数,看被人用的什么(好家伙又省了一步)
卷积层 + 池化层 + 全连接层
为什么要使用卷积
卷积层的两个优势(对比只有全连接层)
参数共享 减少计算量
没有卷积,参数很多(1200w )训练量
加入过滤器 参数很少了(5*5)
稀疏连接
元素连接的关系 不是所有关联的
如下图中的一个框个过滤器 映射到结果中的一个格子 和其他的没有关联关系了,特征于特征(格子和格子)之间没有过多的关联
为什么要进行事例研究
视觉方向的网络迁移很简单
1 如 识别猫的网络 迁移到 识别狗 ,人,车
下面一章就可以开始看论文了
Classic networks(经典网络)
每一次卷积池化图像都会缩小
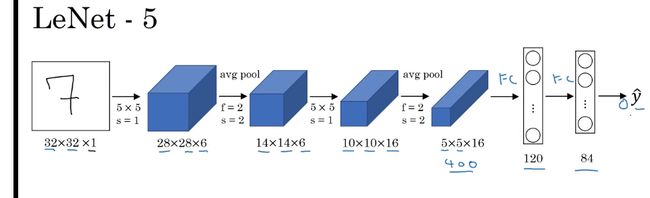
LeNet-5
结构
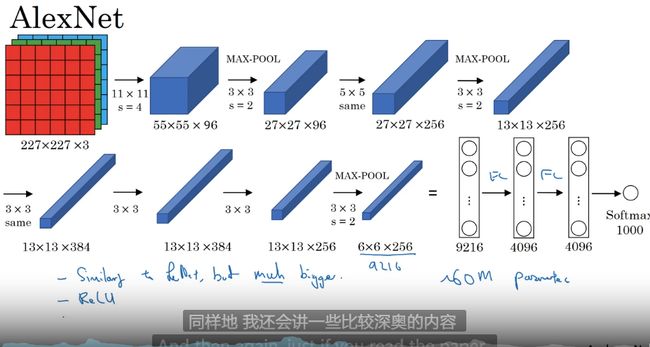
AlexNet
结构
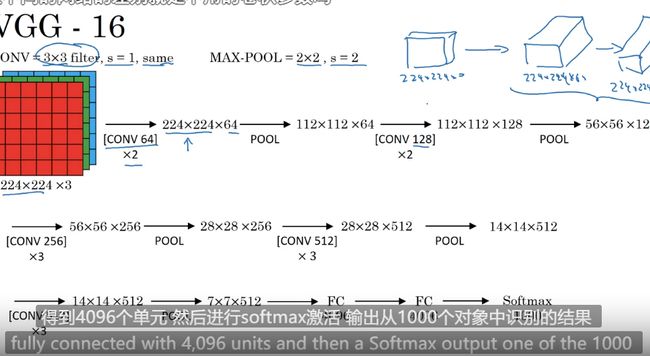
VGG
结构
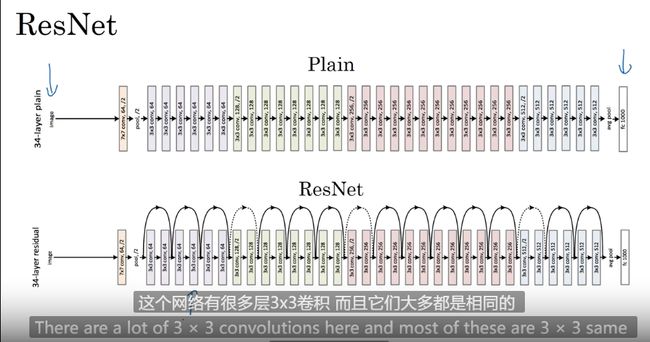
ResNet 残差网络
很深的网络很难训练因为存在梯度消失和梯度爆炸
CNN中深度可能有几种情况,这儿总结一下。
- 深度:指的是网络的层数,有时也称为网络的深度
- 卷积层的深度:卷积核个数。需要和通道数做区别,通道数指的是层数,一个卷积核的通道数与它进行卷积的输入必须是相同。
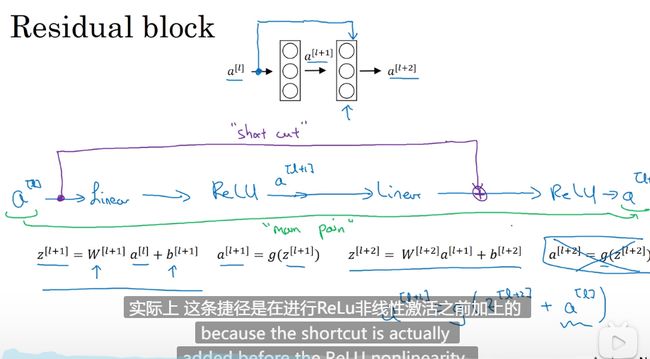
远眺连接
ResNet 模型 何凯明 使得 模型可以很多层的叠加
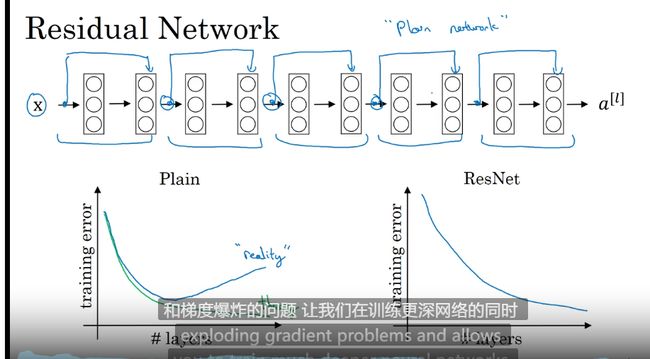
正常的达到峰值后继续迭代错误会增多效果会更差ResNet 模型 解决了这个问题
通过残差块
残差网络为什么有用?
底层原因:残差学习恒等函数非常容易,可以提升网络性能
对比
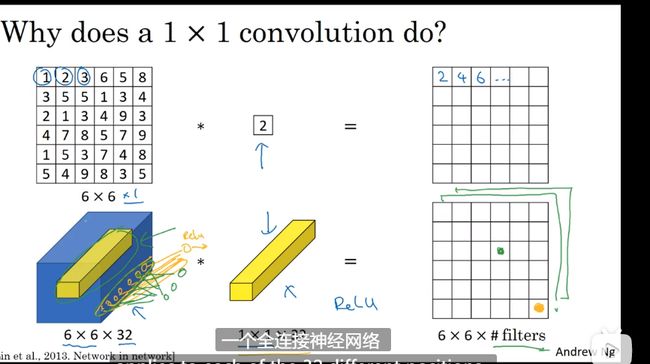
网络中的网络以及1*1 卷积
1*1 的卷积单元可以理解为 全部应用了一个神经网络
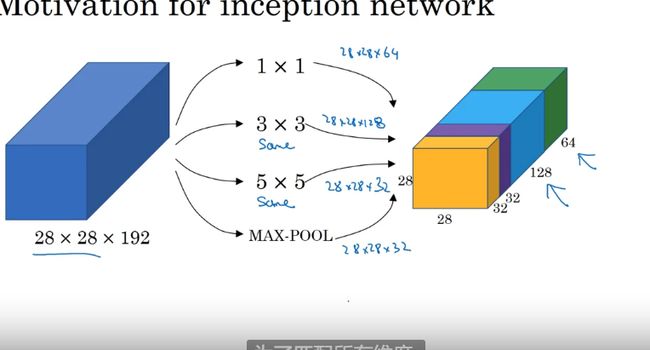
谷歌Inception 网络
1*1 卷积构建Inception 网络
压缩信道
作用:不想决定池化层是使用1*1 3*3 还是 5*5 的过滤器 就使用Inception 使用各种类型的过滤器 只需要把输出连接起来
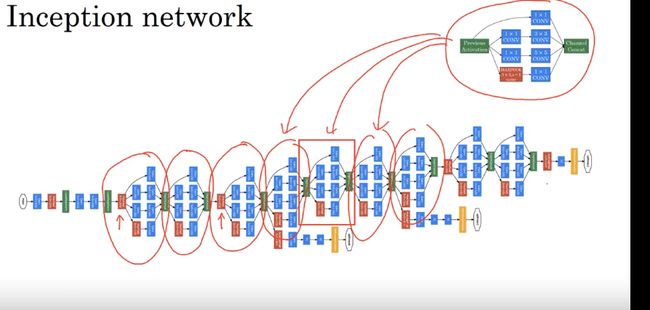
Inception 网络
这些分支的作用 给最后的softmax(推理层) 层做一个补充
使用开源的实现方案
gitHup 使用
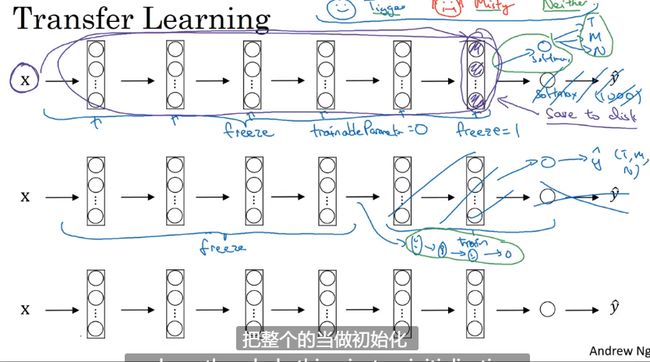
迁移学习
使用预训练模型 别人训练好的模型
冻结一部分网络 训练 如果数据少 如果多的话少冻结一些
数据扩充
1 镜像对称和随机剪裁
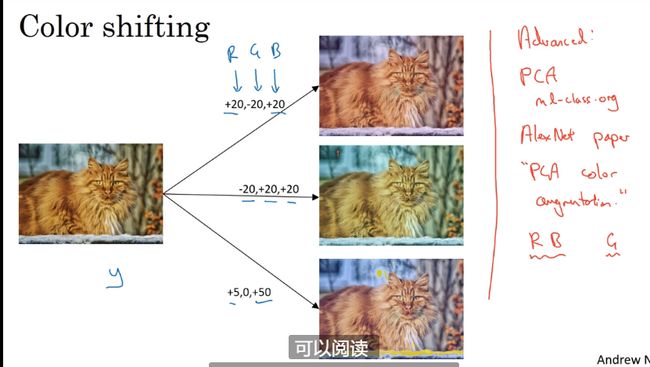
2 色彩转换
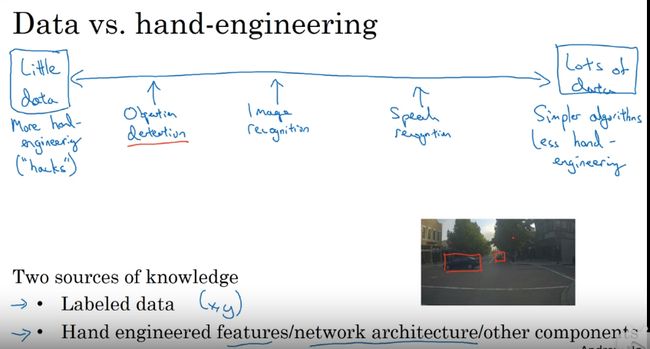
计算机视觉现状
少数据的地方应用到大数据的地方 —> 泛化
没有标注数据的时候考虑手工工程
10-corp 造数据
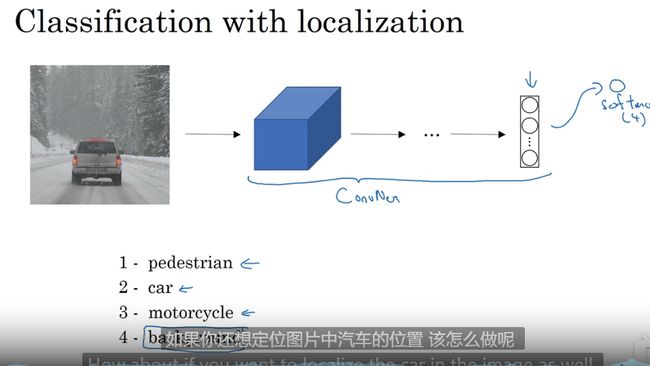
目标定位
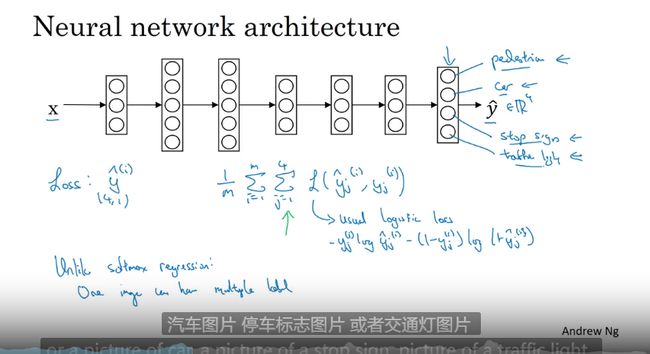
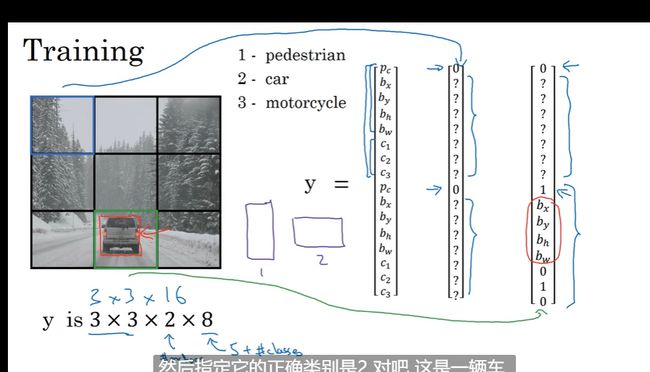
例子: 车辆预测 分类模型
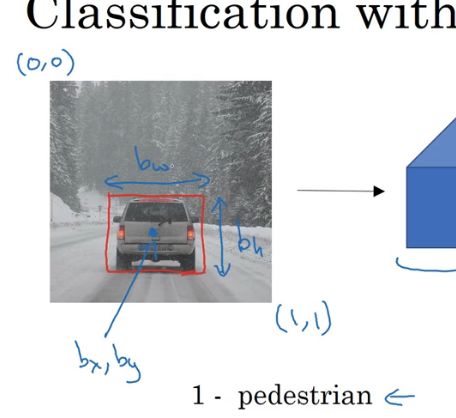
输出类型外还有输出位置框 bx,by,bh,bw
回归任务
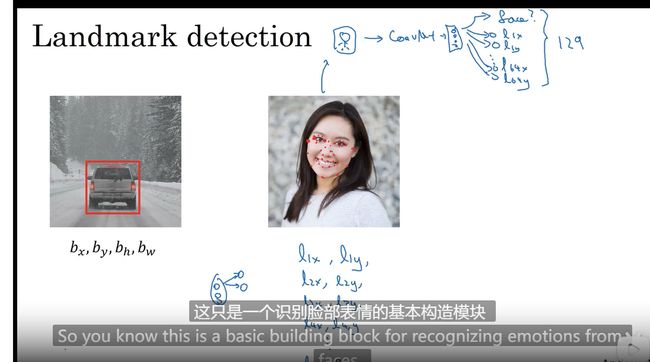
特征点检测
神经网络识别 特征的坐标
列子: 人脸特征点检测 129 个特征点检测
批量添加输出单元,输出要识别的各个特征点的坐标
目标检测
滑动窗口目标检测
1 先输入剪裁过只有车的图片
2 检测框卷积滑动
3 加大检测框
缺点:计算成本
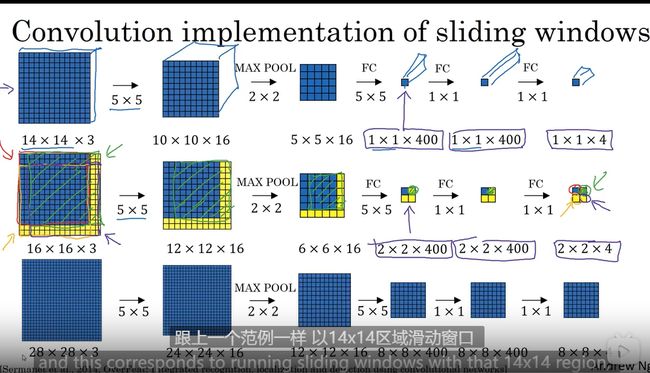
滑动窗口目标检测实践
第一 全连接层转化为卷积层
![]()
输出层在左上角
Bounding Box 预测
比卷积滑动窗口更快 ,但不能输出最精准的边界框
YOLO 算法得到更精准的框
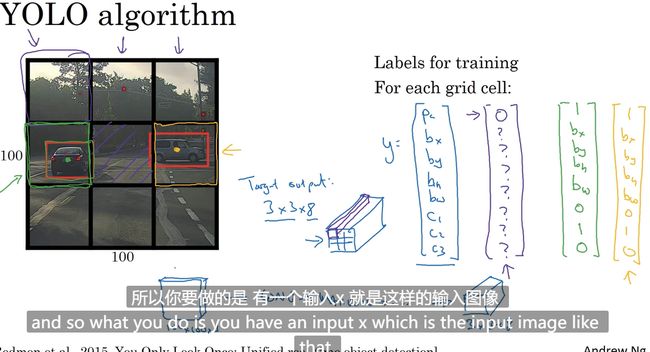
网格分割 图片
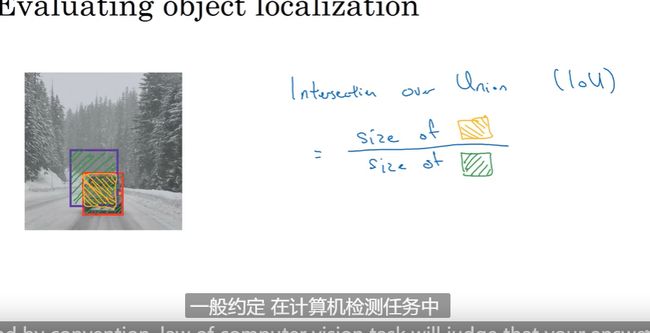
交并比—IOU
下图中红框为标注部分,紫框是模型检测部分
IOU Intersection over Union
计算两个边界框交际并集只比
交 集 并 集 \frac{交集}{并集} 并集交集
一般IOU 大于0.5 就是检测正确 完美情况为1
非极大值抑制
通过算法高亮正确的检测框去变暗去除多余的检测框
Anchor Boxes
一个格子可以检测多个对象的方法
一个横向一个纵向的框
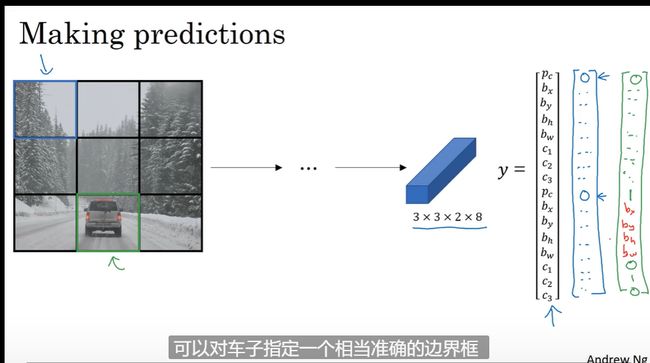
YOLO算法
推理预测
候选区域
R-CNN 带区域的卷积网络 :先通过 分割算法 分割去除一些肯定没有的区域
什么是人脸识别
验证和识别
人脸验证有一定难度在于准确率 在于一次学习问题
One-Shot 学习
人脸相似度计算 设定阈值 大于阈值不是一个人小于则是一个人
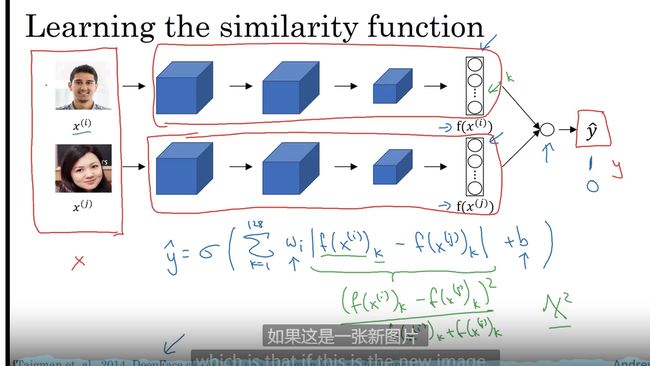
Siamese 网络
人脸图片编码
Triplet 损失
三元组损失
面部验证与二分类
人脸识别问题转化为二分类问题
什么是神经风格转换
图片风格迁移 — 相片滤镜
卷积提取特征
什么是深度卷积网络
寻找接受域
每一层的卷积的范围不断放大
第一层检测边缘 第二层 检测质地 第三层一些复杂 。。。。。
代价函数
需要定义一个代价函数
定义带教函数
J ( G ) = α J c o n t e n t ( C , G ) + β J s t y l e ( S , G ) J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G) J(G)=αJcontent(C,G)+βJstyle(S,G)
使用预训练的卷积模型 比如VGG模型
风格代价函数
检查风格图片相关性 比如垂直风格
一维到三位推广
一些总结
为什么选择序列模型
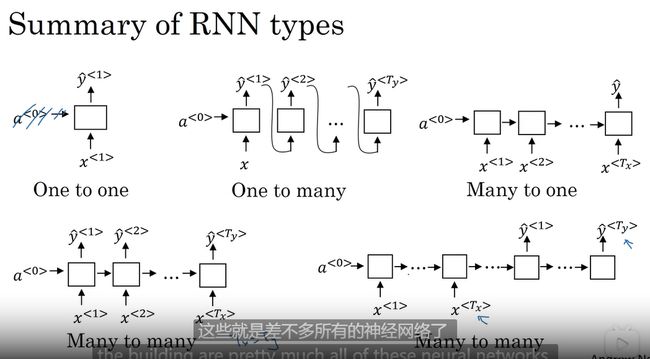
序列模型也有很多不同的类型
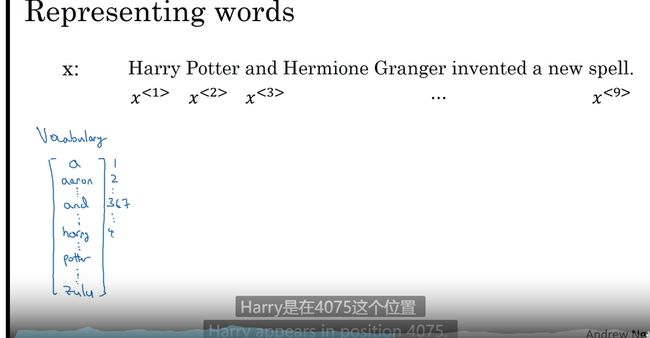
数学符号
例子: NLP
词典建立
3w-5w 词小型的 大型最大可能100w
one-hot
这里用了一个10000 维的向量表示一个一万的词的词典
每个词在指定位置有对应关系 0 不存在 1 存在 UNK 未收录单词 全部为后面矩阵计算做准备
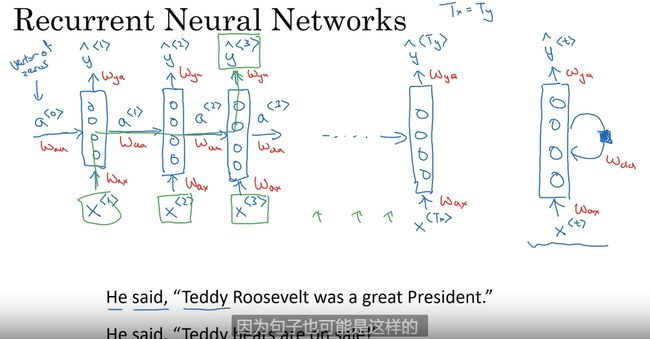
循环神经网络 RNN
循环神经网络 广泛用于NLP方向
比如说需要得到 Teddy 这个人名 需要通过时序模型结合上下文看
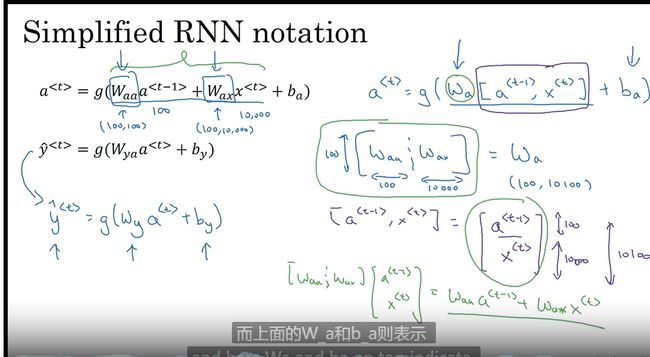
激活函数&损失函数
a 1 = g ( w a a 0 + w a x 1 + b ) y ^ 1 = h ( w y a 1 + b y ) a^1 = g(w{aa}^0+w_{ax}^1+b) \\\hat{y}^1 = h(w_{ya}^1+b_y) a1=g(waa0+wax1+b)y^1=h(wya1+by)
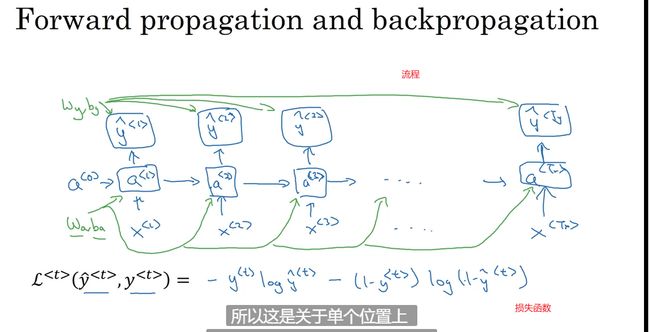
通过时间的反向传播
框架中反向传播是自动进行的,但还是了解一下最好
通过时间(穿越时间)的反向传播
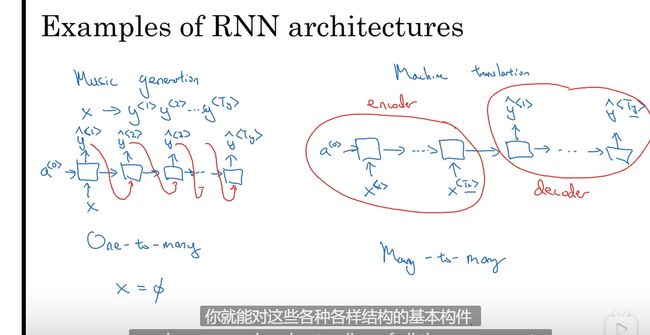
不同类型的循环神经网络 -RNN
循环神经网络不合理的有效性
基本的RNN 一个输入对应一个输出
例子: 语言翻译 输入句子和输出句子长度很可能不一致
不再每个节点上有输入而是RNN 网络读完整个句子
多个输入一个输出
或者一个输入多个输出
总结各个结构的RNN
一对一 标准的网络结构 不需要RNN 也可
一对多 如音乐生成 序列生成
多对一 如情感分类
多对多 机器翻译
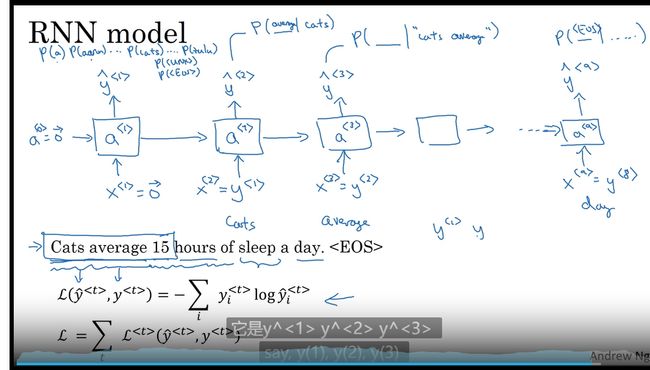
语言模型和序列生成
语音识别系统
softmax 预测每个词的概率
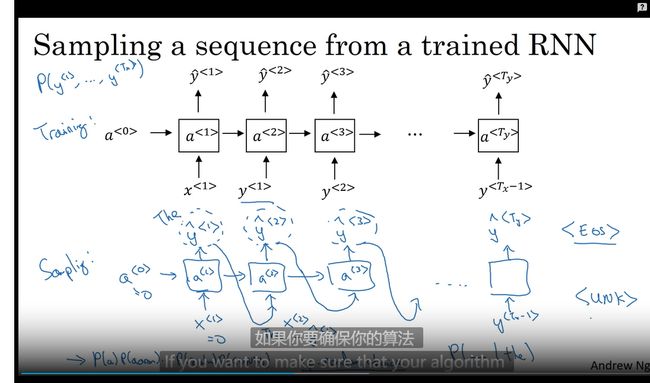
新序列采样
将语音转化为新的字符序列 从字符字典中取到对应的放入
但现在更多的是基于词汇的而不是基于字符字母的词典
带有神经网络的梯度消失
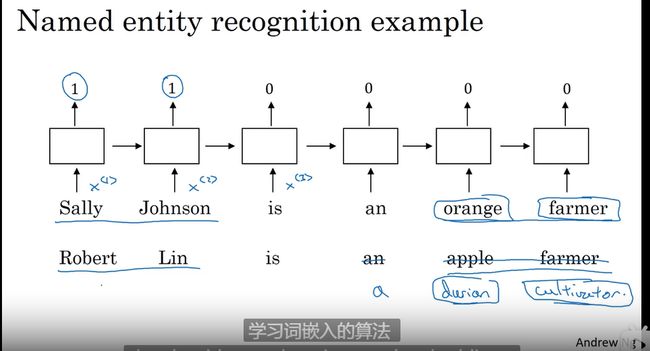
命名识别识别
RNN 有着巨大缺陷
梯度消失& 梯度爆炸 --很深的网络会有这个问题
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mmuwkKGO-1651913336027)(C:\Users\renoy\AppData\Roaming\Typora\typora-user-images\image-20220506111131529.png)]、
梯度爆炸比较鲁棒的解决方案
梯度裁剪
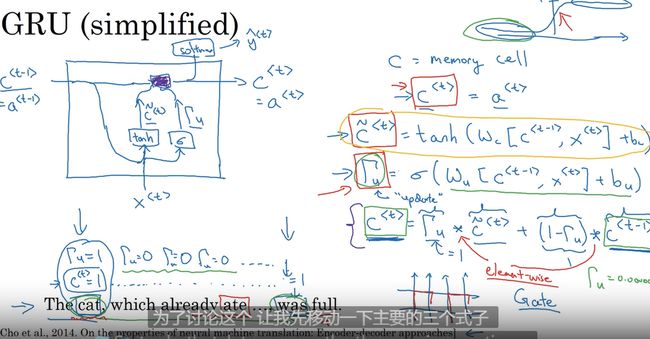
GRU 单元 门循环控制单元
改善梯度消失
在保留长期序列信息下减少梯度消失问题
Γ 表 示 门 大 写 的 γ \Gamma 表示门 大写的\gamma Γ表示门大写的γ
门控循环单元 改变了隐藏层 捕捉深层链接 改善了梯度消失问题
记忆细胞 GRU 输出激活值
GRU 输入上一个时间单元
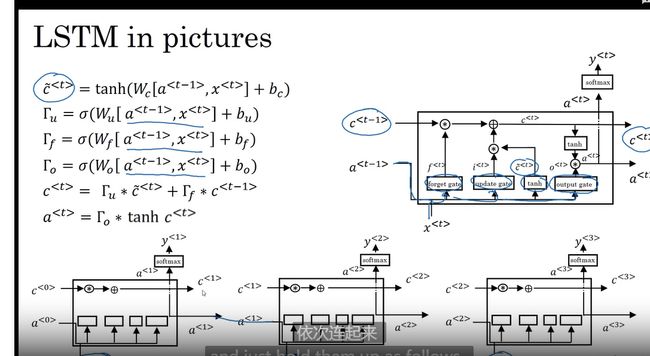
长短期记忆(LSTM) 更优的选择
比GRU 更有效 是GRU 的更强大的通用版本
GRU 有两个门 LSTM 是三个门
结合更新和遗忘门的概念
update forget output
对比
流程
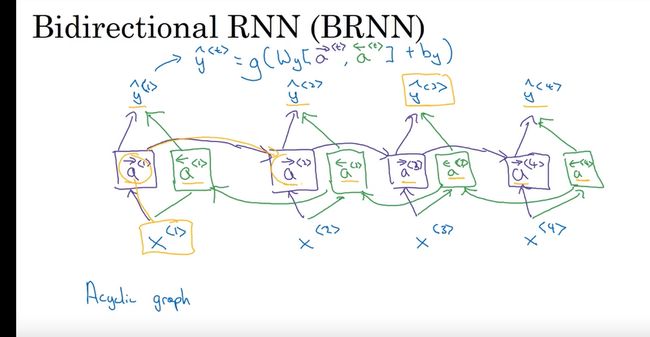
bidirectional RNN 双向RNN BRNN
更好的构建RNN 方法 BRNN
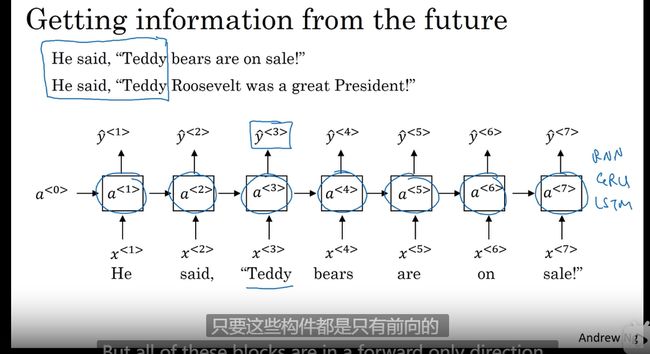
不仅可以获得过去的数据还能获得未来的数据
在仅根据之前的数据无法进行预测的时候可以加入后面的数据一起预测
对比
原始RNN 都是向前的只能获得前面的数据
**BRNN **
加入了一个反向序列
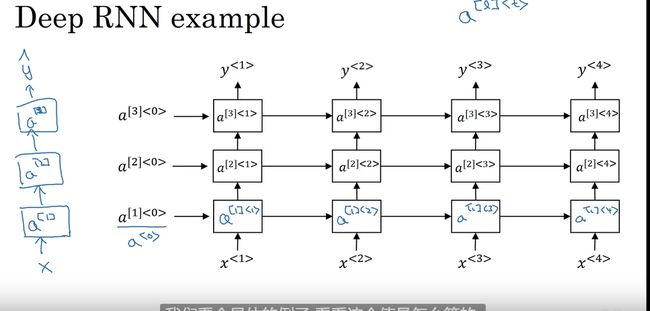
深层循环神经网络 Deep RNN
另一种RNN 升级版
有三个隐层的网络
因为RNN 包含时间序列所以无法有太多的隐层结构 计算资源很大
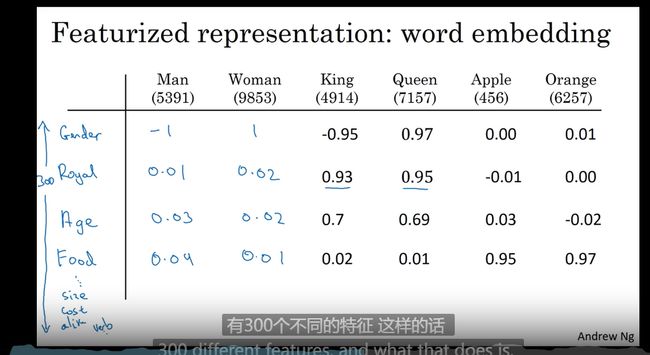
词汇表征
one-hot 表示法
每个词都是字典里面唯一的,用向量表示
缺点 每个词是孤立的,对相关词的泛化性不强
词的相关性 权重
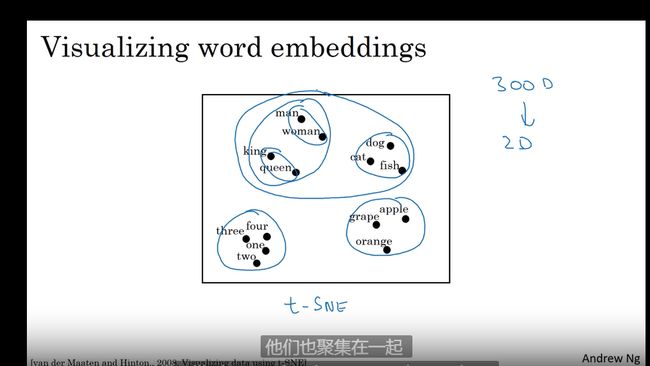
特征可视化算法 t-SNE算法
词嵌入
使用词嵌入
词嵌入是NLP 的重要概念
作用 可以将同类的词聚类使用
通过大量无标签的文本进行词嵌入 (无监督?)
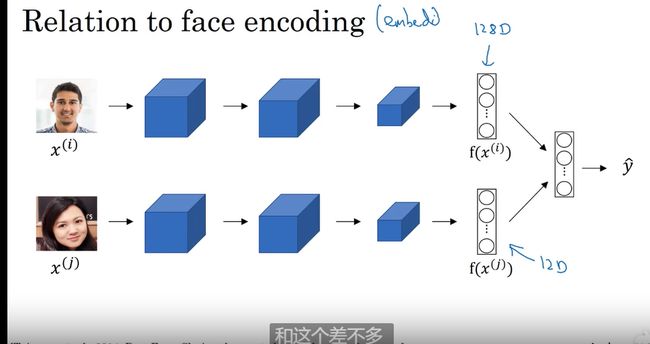
词嵌入和人脸编码之前有一些关联
人脸编码 : 通过比对128 维的比对是否是一个人
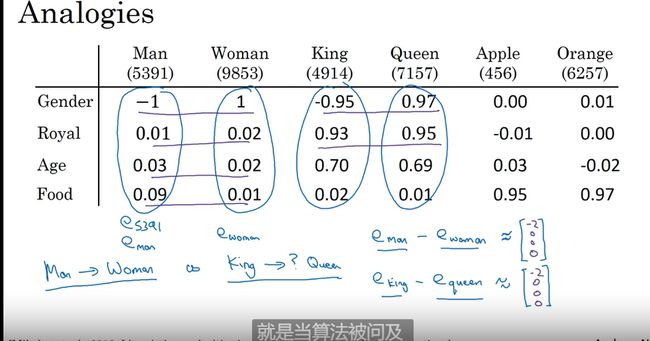
词嵌入的特性
帮助类比推理
词向量
余弦相似度
余弦相似度对这种类比工作效果很不错 欧式距离也可以不过没有余弦用的多
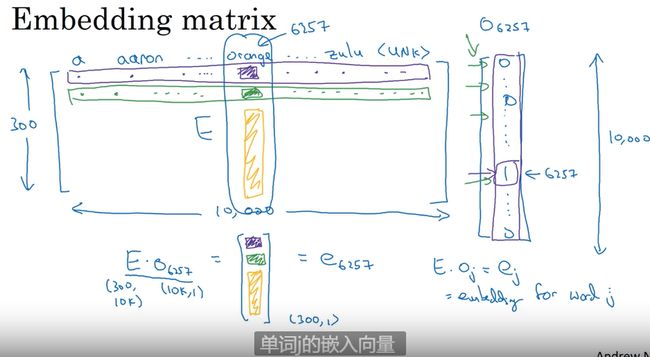
嵌入矩阵
词嵌入实现 —> 嵌入矩阵
计算实现效率很低 ,因为 one-hot 矩阵的维度非常多,并且基本所有元素都是0,所以矩阵相乘效率很低
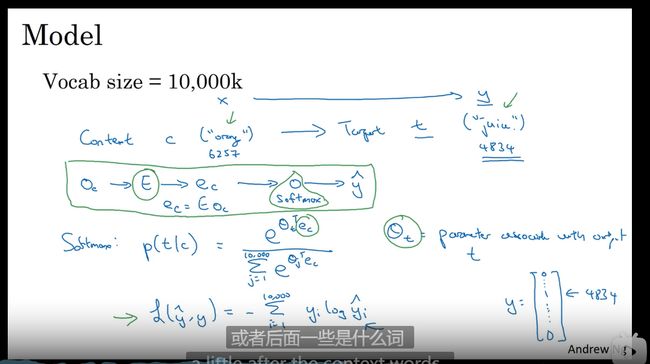
学习词嵌入
Word2Vec
一种简单=高效的计算方式
预测
分类器提速 树形结构
如何对上下文c 进行采样?
1 均匀且随机地采样 有问题 停用词那些
负采样
巧妙的进行采样
一个监督学习模型
核心作用降低学习成本将其转化为 二分类问题
下载他人的词向量是一个很好的方法
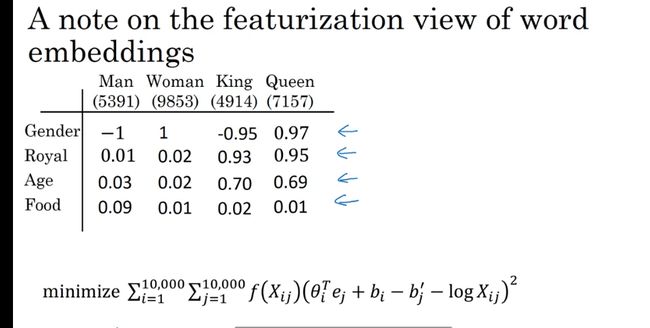
GloVe 词向量 算法
用的不是很多
情绪分类
NLP 的重要方向
如根据评价评星
问题
标记的训练集没有那么多
使用词向量更准确
使用RNN
词嵌入除偏
大量的数据学习可能学到一些不好的东西 比如 男性–> 医生 女性—> 护士 黑人–> 穷 白人—> 富
偏见趋势
基础模型
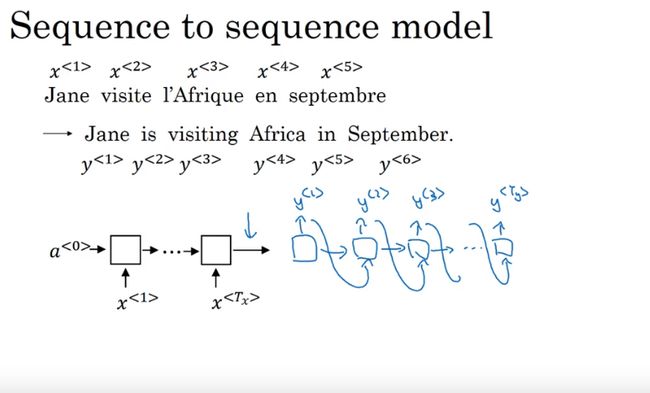
sequence2sequence(序列2序列) model
如翻译模型
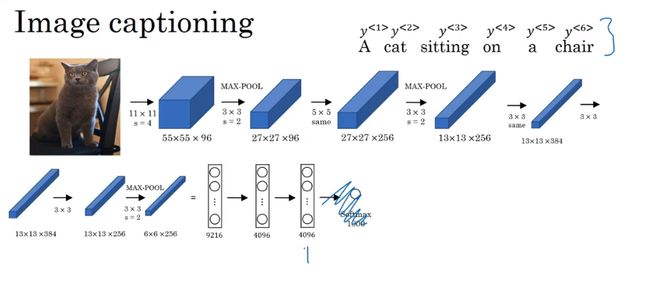
imahe2sequence 图像2序列
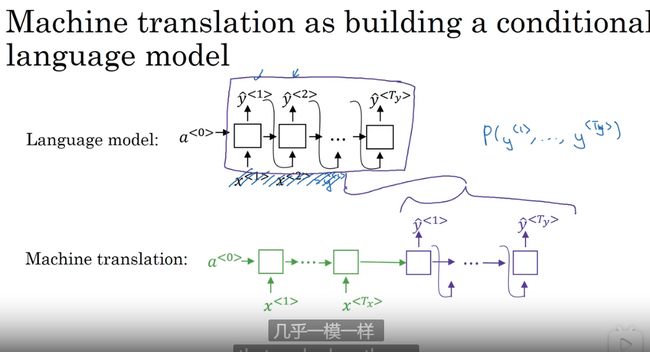
选择 最可能的句子
对比语言模型和机器翻译
几乎一样
算法搜索最大可能性
为什么不用贪心搜索 gready search
第一 每次挑选一个最佳值 局部最优全局可能不是
第二 计算量大
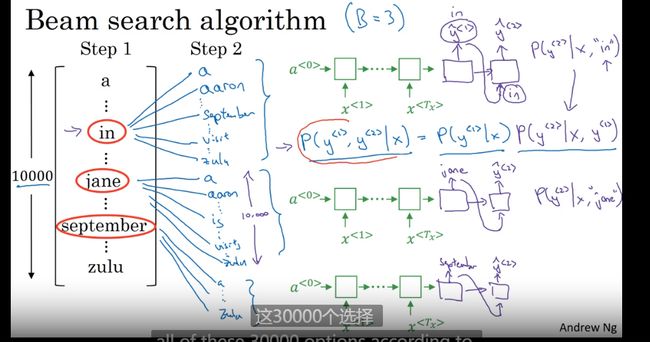
定向搜索 – 集束搜索
例子语音识别
集束宽
每次考虑多值 得到概率
改进定向搜索
改变束宽的大小
定向搜索的误差分析
评估误差 来自RNN 还是束搜索算法
Case1 是束搜索算法 的问题
Case 2 是RNN 的问题
Bleu 得分
机器翻译的准确性怎么衡量? 没有固定值
通过Bleu 来衡量
观察输出的每一个词
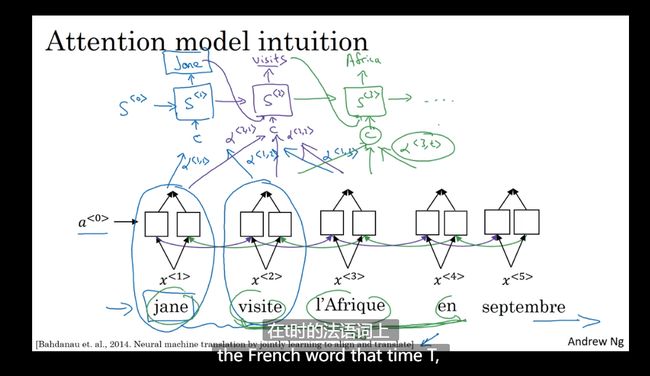
注意力模型直观理解
使得RNN 运行得更好
不同块上放不同注意力
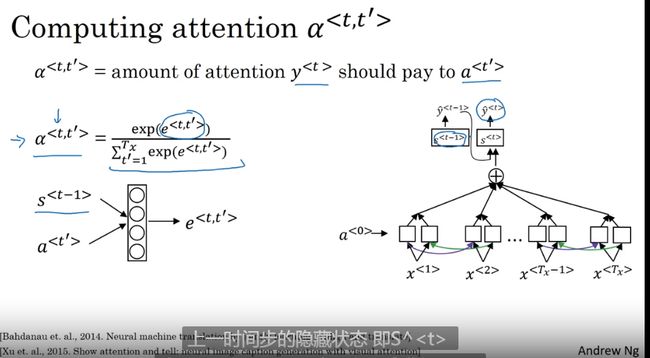
使用注意力机制 计算注意力
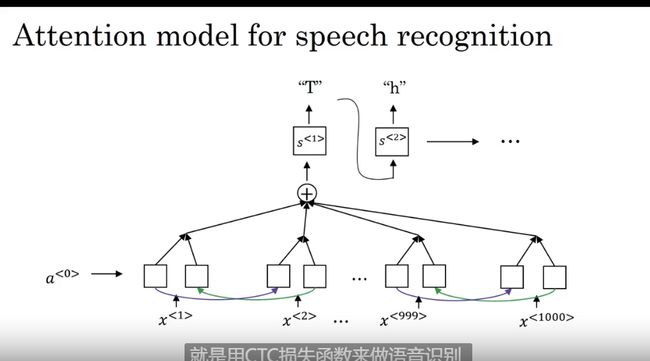
语音辨识
seq2seq 模型在语音识别方面的应用很有生肖
语音转文本
音位构建的系统被end-to-end 端到端模型取代
注意力机制应用其中
CTC 做语音识别
Connectionist temporal classification)
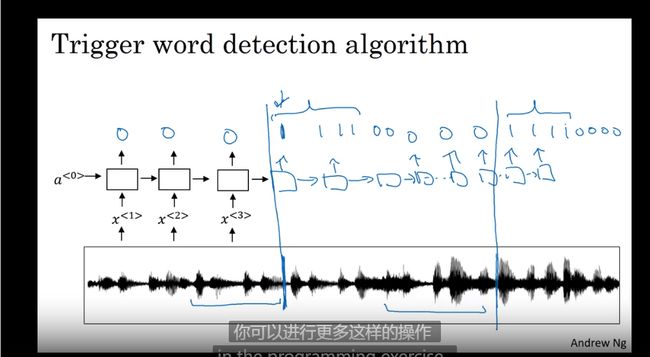
触发字检测
语音设备的唤醒词 语音助手