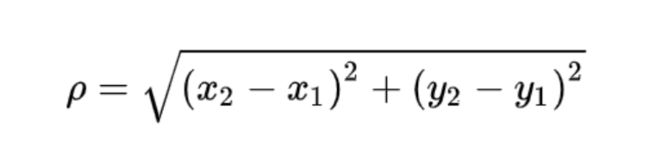K-means聚类算法原理及python具体实现

1 快速理解

• K 均值聚类算法 K-means Clustering Algorithm

• k-means算法又名k均值算法。K-means算法中的k表示的是聚类为k个簇，means代表取每一 个聚类中数据值的均值作为该簇的中心，或者称为质心，即用每-一个的类的质心对该簇进行描述。

• 其算法思想大致为:先从样本集中随机选取k个样本作为簇中心，并计算所有样本与这k个“簇中心”的距离，对于每一个样本， 将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。

• 根据以上描述,我们大致可以猜测到实现kmeans算法的主要四点：
  (1) 簇个数k的选择
  (2) 各个样本点到“簇中心的距离
  (3) 根据新划分的簇，更新"簇中心”
  (4) 重复上述2、 3过程，直至"簇中心"没有移动

• 优缺点：
  优点: 容易实现
  缺点: 可能收敛到局部最小值， 在大规模数据上收敛较慢

1.1 算法步骤

• 步骤：
  1、先定义总共有多少个类/簇【k的值可以自己指定】
  2、将每个簇心，随机定在一个点上
  3、将每一个簇找到其所有关联点的中心点（取每一个点坐标的平均值）
  4、设置上述点为新的簇心
  5、重复上述步骤，直到每个簇所拥有的点不变

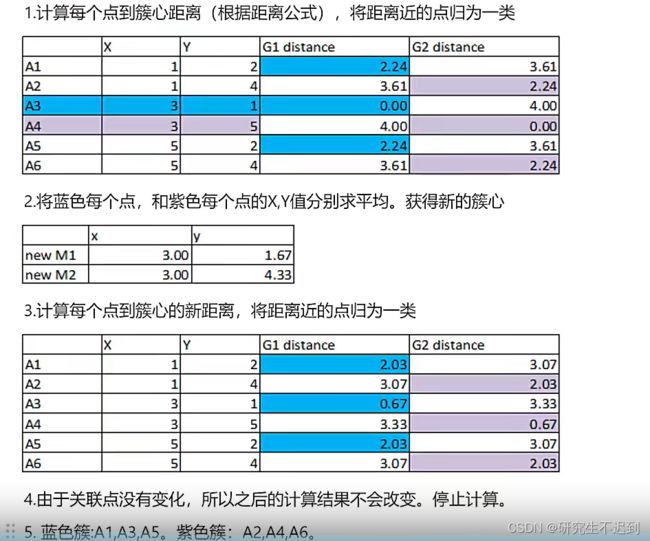
1.2 一个例子

1. 计算每个点到簇心的距离，使用的是欧式距离（k-means算法是基于欧式距离的）；此时是A1 A3 A5归为一类（蓝色），且A3是簇心；A2 A4 A6归为一类（紫色），且A4是簇心
2. 分别计算蓝色和紫色类中的avg(x)和avg(y)， 那作为新的簇心；
3. 计算每个点到新的簇心的距离，并且将距离近的归为一类。此时蓝色类和紫色类中的点还是原来的点，所以循环停止。
4. 最后输出簇心以及类中其他的点

2 K-means步骤详解

2.1 K值的选择

1. K值 = 分为几类 = 簇组数量 = 质心数量 【由用户给出】
2. 每次更新，K值保持不变

2.2 距离度量

• 计算每个点与簇心之间距离的度量策略。
• 在欧式空间采用的是欧式距离，在处理文档中采用的是余弦相似度，有的时候也采用曼哈顿距离作为度量，不同情况度量方法不同。

2.3 新质心的计算

• 对于分类之后产生的k个簇，分别计算簇内其他点距离均值最小的点作为质心

2.4 停止条件

• 如果分类中的样本与上次分类结果一致，那么就停止k-means

3 K-means算法实现

3.1 创建数据集

• dataset是一个list

def createDataSet():
    return [[1, 1], [1, 2], [2, 1], [6, 4], [6, 3], [5, 4]]


if __name__ == '__main__':
    dataset = createDataSet()  # type(dataset)='list'

3.2 kmeans函数实现

• 作用：实现k-means算法

# k-means 算法实现
def kmeans(dataSet, k):
    # (1) 随机选定k个质心
    centroids = random.sample(dataSet, k)
    print("输出两个质心", centroids)

    # (2) 计算样本值到质心之间的距离，直到质心的位置不再改变
    changed, newCentroids = Update_cen(dataSet, centroids, k)
    while np.any(changed):
        changed, newCentroids = Update_cen(dataSet, centroids, k)

    centroids = sorted(newCentroids.tolist())

    # (3) 根据最终的质心，计算每个集群的样本
    cluster = []
    dis = Distance(dataSet, centroids, k)  # 调用欧拉距离
    minIndex = np.argmin(dis, axis=1)
    for i in range(k):
        cluster.append([])
    for i, j in enumerate(minIndex):  # enumerate()可同时遍历索引和遍历元素
        cluster[j].append(dataSet[i])

    return centroids, cluster

3.2.1 random.sample(sequence, k)

表示从指定序列sequence中，随机获取k个数据元素，随机排列，并以列表的形式返回。
*注sample不会修改原有序列

• 例如代码：

    dataset = [[1, 1], [1, 2], [2, 1], [6, 4], [6, 3], [5, 4]]
    data = random.sample(dataset, k=4)
    print(data)

• 输出结果：

	[[1, 2], [6, 4], [5, 4], [2, 1]]

3.2.2 np.all()

• 用于判断整个数组中的元素的值是否全部满足条件，如果满足条件返回True，否则返回Flase

3.2.3 np.any()

• 任意一个元素为True，输出为True。

3.3 Updata_cen 函数实现

• 作用：更新质心

3.3.1 np.argmin(data, axis=None, out=None)

• 求data在指定axis维度上最小值对应的位置索引（索引从0开始）。（若有多个相同的最小值，则返回第一个）
• data可以是list类型，可以是array类型

a=np.array([[1, 5, 5, 2],
              [9, 6, 2, 8],
              [3, 7, 9, 1]])
min_a0 = np.argmin(a, axis=0)
min_a0
array([0, 0, 1, 2], dtype=int64)
min_a1 = np.argmin(a, axis=1)
min_a1
array([0, 2, 3], dtype=int64)

3.3.2 df.groupby().mean()

• 根据DataFrame的一个属性进行分组，然后求均值

newCentroids = pd.DataFrame(dataSet).groupby(minIndex).mean()

• 比如说上面代码，先把数据集按照minIndex索引分类，因为minIndex索引只有0和1，因此分为两类。
• 然后求每一个类中的均值，作为新的x和新的y

3.4 Distance 函数实现

• 作用：计算欧式距离

# 计算欧式距离
def Distance(dataSet, centroids, k) -> np.array():
    dis = []
    for data in dataSet:
        diff = np.tile(data, (k, 1)) - centroids  # 行数上复制k份，方便作差
        temp1 = diff ** 2
        temp2 = np.sum(temp1, axis=1)  # 按行相加
        dis_temp = temp2 ** 0.5
        dis.append(dis_temp)
    dis = np.array(dis)  # 转换为一个array类型
    return dis

3.4.1 np.tile(data, (x, y))

• 此函数是扩展函数，data是要扩展的数据，类型为np类型数组，x：扩展行数，y：扩展列数
• 代码测试：

import numpy as np
arr1 = np.array([4, 2])
arr1
array([4, 2])
np.tile(arr1, (6, 1))
array([[4, 2],
       [4, 2],
       [4, 2],
       [4, 2],
       [4, 2],
       [4, 2]])
np.tile(arr1, (6, 2))
array([[4, 2, 4, 2],
       [4, 2, 4, 2],
       [4, 2, 4, 2],
       [4, 2, 4, 2],
       [4, 2, 4, 2],
       [4, 2, 4, 2]])
arr1
array([4, 2])

3.4.2 计算欧式距离

1. 这里质心是k=2个，所以说需要np.tile()函数复制k份，然后就可以一次性把每一个样本点到这k=2个质心的欧式距离都算出来了。【k是用户指定值】

【此公式适用于二维空间计算欧式距离，多维空间需要推广】

2. 对应维度相减再求和，再开方。
   

3.4.3 np.sum(数组，axis=None)

• 求和函数， axis默认为None，也就是求整个数组的和
• 指定axis=0按列求和，axis=1按行求和

import numpy as np
data = np.arange(6).reshape(2, 3)
data
array([[0, 1, 2],
       [3, 4, 5]])
np.sum(data)
15
np.sum(data, axis=0)
array([3, 5, 7])
np.sum(data, axis=1)
array([ 3, 12])

4 代码

import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


# 计算欧式距离
def Distance(dataSet, centroids, k) -> np.array:
    dis = []
    for data in dataSet:
        diff = np.tile(data, (k, 1)) - centroids  # 行数上复制k份，方便作差
        temp1 = diff ** 2
        temp2 = np.sum(temp1, axis=1)  # 按行相加
        dis_temp = temp2 ** 0.5
        dis.append(dis_temp)
    dis = np.array(dis)  # 转换为一个array类型
    return dis


# 更新质心
def Update_cen(dataSet, centroids, k):
    # 计算每个样本到质心的距离，返回值是array数组
    distance = Distance(dataSet, centroids, k)
    # print("输出所有样本到质心的距离：", distance)
    # 分组并计算新的质心
    minIndex = np.argmin(distance, axis=1)  # axis=1 返回每行最小值的索引
    # print("输出最小值索引", minIndex)
    newCentroids = pd.DataFrame(dataSet).groupby(minIndex).mean()
    # print("新的质心(dataframe)：", newCentroids)
    newCentroids = newCentroids.values
    # print("新的质心(值）：", newCentroids)

    # 计算变化量
    changed = newCentroids - centroids
    return changed, newCentroids


# k-means 算法实现
def kmeans(dataSet, k):
    # (1) 随机选定k个质心
    centroids = random.sample(dataSet, k)
    print("随机选定两个质心：", centroids)

    # (2) 计算样本值到质心之间的距离，直到质心的位置不再改变
    changed, newCentroids = Update_cen(dataSet, centroids, k)
    while np.any(changed):
        changed, newCentroids = Update_cen(dataSet, newCentroids, k)
    centroids = sorted(newCentroids.tolist())

    # (3) 根据最终的质心，计算每个集群的样本
    cluster = []
    dis = Distance(dataSet, centroids, k)  # 调用欧拉距离
    minIndex = np.argmin(dis, axis=1)
    for i in range(k):
        cluster.append([])
    for i, j in enumerate(minIndex):  # enumerate()可同时遍历索引和遍历元素
        cluster[j].append(dataSet[i])

    return centroids, cluster


# 创建数据集
def createDataSet():
    return [[1, 1], [1, 2], [2, 1], [6, 4], [6, 3], [5, 4]]


if __name__ == '__main__':
    dataset = createDataSet()  # type(dataset)='list'
    centroids, cluster = kmeans(dataset, 2)  # 2 代表的是分为2类=2个质心
    print('质心为：%s' % centroids)
    print('集群为：%s' % cluster)
    # x = list(np.array(dataset).T[0])
    # y = list(np.array(dataset).T[1])
    plt.scatter(list(np.array(dataset).T[0]), list(np.array(dataset).T[1]), marker='o', color='green', label="数据集" )
    plt.scatter(list(np.array(centroids).T[0]), list(np.array(centroids).T[1]), marker='x', color='red', label="质心")
    plt.show()