URAL 1988 - Planet Ocean Landing【几何&三分答案】

【题意】

在一个星球（是一个球体）表面有一个飞机（坐标(x1,y1,z1)，原点是星球中心），在空中有一个空间站（坐标(x2,y2,z2)），所有值均小于100，现在要使飞机与空间站相遇，飞机的速度是1，空间站速度是v，v是小于等于100的整数。飞机只能沿星球表面飞，而空间站可以任意飞，当然不能进入星球内部。

 

【解答】

首先可以把三维图形转化为二维的，也就是飞机，空间站，原点确定的那一个平面，

为什么是含原点的平面？我们不妨把球体旋转一下，把飞机的初始位置固定在球体的最上边，空间站在球的侧边的上空，显然只有沿过原点平面的路线是最短的。

 

现在能确定三个参量，飞机（设为点A）的高度p，空间站（设为点B）的高度q，以及飞机原点的直线，空间站原点的直线的夹角（角AOB）

求夹角可以用点积 p*q = |p|*|q|*cos<p,q>

注意用叉积=|p|*|q|*sin<p,q>是不推荐的，因为使用asin()函数求角度时，它不可能返回大于pi/2的角度（可以联系反三角函数图像），使用acos()则不会出现这种问题。【差错了三个小时发现是跪在了这里Σ(っ °Д °;)っ 】

现在可以转化为二维图了

 

我们不妨设空间站在x轴上，飞机在x轴上方，因为夹角一定小于180度，所以飞机在x轴上方或者下方是等价的。我们假设在x轴上方。

 

 

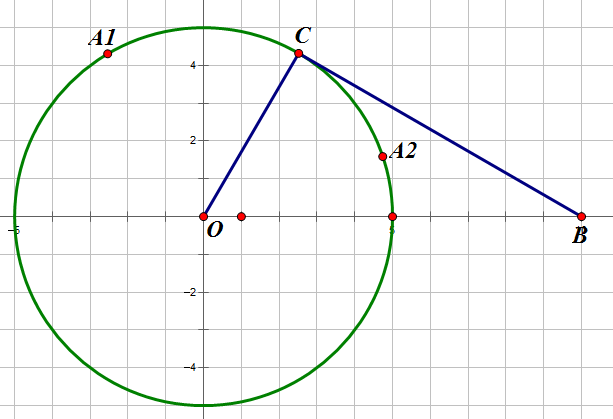
这样成功转化为容易对其思考的二维图形

 

下面就是如何选择相遇点的问题，假设相遇在第一个A1到C点之间，那么空间站一定是先沿圆的切线BC走，再沿弧CA1走，

 

一开始想并不是沿弧走，而是沿折现走，比如说下边这个图

沿ACE走，显然走ABDE更要近一些（三角形一边比另外两边和要短），以此类推，还是走弧最近。

假设相遇点在A2处，那么空间站B就沿之间走到A2，飞船A就沿弧走到A2即可。

 

寻找相遇点可以使用二分，但发现相遇点从A到D（圆与x轴正半轴交点），花费时间可能是先见减后增的，所以需要三分找时间最小值。

 

三分的框架：

while (l<r)

{

    m1=l+(r-l)/3;

    m2=r-(r-l)/3;

    if(find(m1)<find(m2)) r=m2;

    else l=m1;

}

当然也可以二分时间，这样就可以避免三分了。

 

程序代码：

#include <iostream>

#include <iomanip>

#include <fstream>

#include <stdlib.h>

#include <time.h>

#include<cstring>

#include<cstdio>

#include<vector>

#include<string>

#include<algorithm>

#include <limits.h>

#include<cmath>

#include<map>

#include<queue>

#include<set>

using namespace std;



typedef long long LL;

int i,j,k,n,m,x,y,T,ans,big,cas,num,len;

bool flag;



double ms,sp,fl,si,m1,m2,lenp,lenq,l,r,t1,t2;

int v;

struct node

{

    double x,y,z;

}p,q,s;



double leng(node r)

{

    return sqrt(r.x*r.x+r.y*r.y+r.z*r.z);

}



double sz(double x,double y)

{

    return sqrt(x*x+y*y);

}



double getime(double m)

{

    if (m<=ms)

    {

        sp=sz(lenp*sin(m),lenq-lenp*cos(m)) /v;

        fl=(si-m)*lenp;

        return max(sp,fl);

    }else

    {

        fl=(si-m)*lenp;

        sp=(sz(lenp*sin(ms),lenq-lenp*cos(ms)) + (m-ms)*lenp )/v;

        return max(fl,sp);

    }

}



int main()

{

    scanf("%lf%lf%lf",&p.x,&p.y,&p.z);

    scanf("%lf%lf%lf",&q.x,&q.y,&q.z);

    scanf("%d",&v);



    s.x=p.x*q.x;

    s.y=p.y*q.y;

    s.z=p.z*q.z;



    lenp=leng(p);

    lenq=leng(q);

    si=acos((s.x+s.y+s.z)/lenp/lenq);

    ms=acos(lenp/lenq);

    l=0;

    r=si;

    while (r-l>=1e-10)

    {

        m1=(r+2*l)/3;

         m2=(2*r+l)/3;

         t1=getime(m1);

         t2=getime(m2);



        if (t1>t2) l=m1; else r=m2;

    }



    printf("%.6lf\n",getime(l));



    return 0;

}