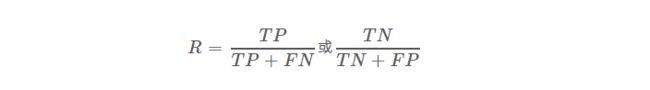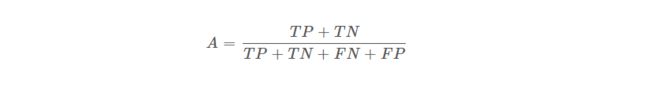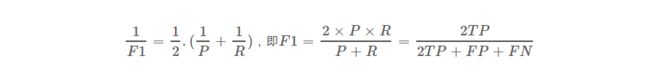机器学习第10天:模型评价方法及代码实现
文章目录
- 一、分类评价指标
-
- 1.精确率(Precision)
- 2.召回率(Recall)
- 3.准确率(Accuracy)
- 4.F1_score
- 二、回归评价指标
-
- 1.平方根误差(RMSE)
- 2.均方误差(MSE)
- 3.平均绝对误差(MAE)
- 4.R方值(R2_score)
这里先引入模型评价相关的概念以及相应的公式,让大家一个大概的理解,知道有这么一回事,在后续文章中我将结合具体实例进行详细的讲解。
一、分类评价指标
混淆矩阵
| 真实\预测 | 正例 | 反例 |
|---|---|---|
| 正例 | TP(真正例) | FN(假反例) |
| 反例 | FP(假正例) | TN(真反例) |
-
TP: 将正例预测为正例(预测正确)
-
FN: 将正例预测为负例(预测错误)
-
FP: 将负例预测为正例(预测错误)
-
TN: 将负例预测为负例(预测正确)
1.精确率(Precision)
定义: 精确率(Precision),是被判定为正例(反例)的样本中,真正的正例样本(反例样本)的比例。举个例子,一个盒子里有20个小球,10个白的10个黑的,现在要找到盒子中的黑球,拿出了8个球其中2个黑6个白的,那么查找精确率为2/6=0.3333。
from sklearn.metrics import precision_score
y_true = [3, 1, 2, 0, 1, 0]
y_pred = [1, 0, 1, 0, 0, 1]
precision_score(y_true, y_pred)
2.召回率(Recall)
定义:召回率(Recall),是被正确分类的正例(反例)样本,占所有正例(反例)样本的比例。举个例子,一个盒子里有20个小球,10个白的10个黑的,现在要找到盒子中的黑球,拿出了8个球其中2个黑6个白的,那么查找召回率为2/10=0.2。
from sklearn.metrics import recall_score
y_true = [3, 1, 2, 0, 1, 0]
y_pred = [1, 0, 1, 0, 0, 1]
recall_score(y_true, y_pred)
3.准确率(Accuracy)
定义: 指的是分类正确的样本数量占样本总数的比例。
import numpy as np
from sklearn.metrics import accuracy_score
y_true = [3, 1, 2, 0, 1, 0]
y_pred = [1, 0, 1, 0, 0, 1]
accuracy_score(y_true, y_pred)
注:逻辑回归LogisticRegression.score()与K-邻近算法KNeighborsClassifier.score()中使用的就是该评价方法。
4.F1_score
定义: 精确率和召回率的调和平均值。
from sklearn.metrics import f1_score
y_true = [3, 1, 2, 0, 1, 0]
y_pred = [1, 0, 1, 0, 0, 1]
f1_score(y_true, y_pred)
二、回归评价指标
1.平方根误差(RMSE)
平方根误差(RMSE),其又被称为RMSD(root mean square deviation),是回归模型中最常用的评价指标。
公式:
R M S E = M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 RM S E=\sqrt{M S E}= \sqrt{\frac{1}{m}\sum_{i=1}^{m}\left(y_i-\hat{y}_i\right)^{2}} RMSE=MSE=m1i=1∑m(yi−y^i)2
- y i y_i yi是第i个样本的真实值
- y ^ \hat y y^是第i个样本的预测值
- m是样本的个数
代码:
from sklearn.metrics import mean_squared_error
y_true = [1,2,4]
y_pred = [1,3,5]
RMSE = mean_squared_error(y_true,y_pred)**0.5
2.均方误差(MSE)
公式:
M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 M S E=\frac{1}{m}\sum_{i=1}^{m}\left(y_i-\hat{y}_i\right)^{2} MSE=m1i=1∑m(yi−y^i)2
- y i y_i yi是第i个样本的真实值
- y ^ \hat y y^是第i个样本的预测值
- m是样本的个数
代码:
from sklearn.metrics import mean_squared_error
y_true = [1,2,4]
y_pred = [1,3,5]
MSE = mean_squared_error(y_true,y_pred)
3.平均绝对误差(MAE)
公式:
M A E = 1 m ∑ i = 1 m ∣ y i − y ^ i ∣ MAE=\frac{1}{m}\sum_{i=1}^{m}\vert{y_i-\hat{y}_i}\vert MAE=m1i=1∑m∣yi−y^i∣
- y i y_i yi是第i个样本的真实值
- y ^ \hat y y^是第i个样本的预测值
- m是样本的个数
代码:
from sklearn.metrics import mean_absolute_error
y_true = [1,2,4]
y_pred = [1,3,5]
MAE = mean_absolute_error(y_true,y_pred)
4.R方值(R2_score)
公式:
R 2 = 1 − ∑ i = 1 m ( y i − y ^ i ) 2 ∑ i = 1 m ( y i − y ˉ i ) 2 R^2 = 1 - \frac{\sum_{i=1}^{m}(y_i-\hat{y}_i)^2}{\sum_{i=1}^{m}(y_i-\bar{y}_i)^2} R2=1−∑i=1m(yi−yˉi)2∑i=1m(yi−y^i)2
- y i y_i yi是第i个样本的真实值
- y ^ \hat y y^是第i个样本的预测值
- m是样本的个数
代码:
from sklearn.metrics import r2_score
y_true = [1,2,4]
y_pred = [1,3,5]
R2 = r2_score(y_true,y_pred)
注:线性回归LinearRegression.score()中使用的就是该评价方法