matlab应力比法,一种考虑隧道围岩应力分布的强度应力比岩爆判据方法与流程

本发明属于地下工程技术领域,具体涉及一种考虑隧道围岩应力分布的强度应力比岩爆判据方法。

背景技术：

高地应力环境中的深部岩体开挖越来越多，岩爆作为深埋长大隧道的重大工程地质问题之一，其预防与控制问题将越来越突出。准确的岩爆预测有助于在设计和施工中采取相应的工程对策，减少或避免岩爆灾害带来的损失。目前对于岩爆的研究理论较多，但基于岩爆理论及岩爆破坏机制而提出的各种理论预测方法，在工程应用中尚存在准确率偏低的问题，因此，针对岩爆判据的研究具有重要的意义。

目前，工程实际中一般釆用简单分级的方法对岩爆进行预测，其中应力比判据在应变型岩爆的预测中被广泛运用。基于强度理论的应力比岩爆判据多利用工程开挖后岩体所受切向应力或远场最大主应力与围岩单轴抗压强度的比值，包括陶振宇判据，挪威Barton判据，Russense判据，Hoek判据。此外岩爆判据还有能量法，刚度法，岩性法，临界深度法等。由于不能考虑各种因素的综合影响，其结果往往与实际情况出入较大。因此，人们引入了模糊数学方法、灰色系统理论来预测岩爆，并取得了一定的效果，但对各影响因素之间的相互关系很少深入探讨，且预报需人为设定主要因子及各判别因子的权值，但岩爆是一种突发性的复杂灾变过程，专家确定的重要性权值或基于指标值确定的客观权值，很难全面反映影响因素间的相互依赖或相互关联的程度，也限制了它们的应用。神经网络方法、支持向量机方法和距离判别方法等虽然解决了此难题，但它们受知识获取“瓶颈”问题的限制，存在应用局限性。

应变型岩爆主要发生在洞室开挖后切向应力集中的加载过程中，因此，无论是单因素应力比岩爆判据还是多因素非线性预测方法，强度应力比判据常被作为岩爆评价时的关键指标。强度理论主要从岩石的强度和开挖围岩二次集中应力的关系角度出发，简单地以应力相对大小作为破坏判据。但开挖造成的围岩变形破坏不仅依赖于岩体的应力大小，还与应变路径以及它原来的应力历史有关。地下洞室开挖过程中，围岩经历了复杂的应力路径，其围岩切向加载应力在洞壁处较大，并以一定梯度向围岩内部递减，埋深、开挖方式、地质构造等都会对其分布造成影响。因此，单纯考虑围岩应力大小而忽略应力分布的强度判据存在一定的片面性。

综上所述，岩体变形破坏和岩爆过程中应力状态是十分复杂的，在某种意义上具有一定的不确定性，正是由于这种不确定性，简单地以应力大小作为破坏判据是片面的。目前尚未有综合考虑应力大小及分布的岩爆判别方法。

技术实现要素：

本发明的目的是提供一种考虑隧道围岩应力分布的强度应力比岩爆判据方法，以解决上述问题。

本发明解决上述技术问题的技术方案如下：一种考虑隧道围岩应力分布的强度应力比岩爆判据方法，包括以下步骤：

步骤1，提出应力集度的概念，用以表示二次扰动应力在围岩扰动区的集中程度，即围岩应力分布，其物理意义为：反映围岩切向应力由硐壁向围岩内部的衰减变化情况，并利用以下公式计算应力集度，

其中，η用来表示围岩切向的应力集度，式中，R0为开挖洞径，单位m，对于非圆形硐室可以采用当量方法来计算其洞径；σθ为开挖前隧道横截面最大初始应力，单位MPa；σθmax为洞壁切向应力最大值，单位MPa；

步骤2，利用现有的工程数据，得到应力集度、强度应力比及岩爆烈度的实测数据，并将岩爆烈度表示在由强度应力比及应力集度所确定的二维平面内；

步骤3，对岩爆的不同烈度在强度应力比及应力集度所确定的二维平面内进行区间划分，开展强度应力比及应力集度的双参量岩爆烈度经验拟合，并对各烈度区间的拟合结果加以综合量化表达，结合强度应力以及应力集度的大小综合判定岩爆强度。

进一步的，步骤1中应力集度的公式可以进一步简化为

其中，η用来表示围岩切向的应力集度，式中，R0为开挖洞径，单位m，对于非圆形硐室可以采用当量方法来计算其洞径；σθ为开挖前隧道横截面最大初始应力，单位MPa；σθmax为洞壁切向应力最大值，单位MPa。

进一步的，步骤3中结合强度应力以及应力集度的大小综合判定岩爆强度的具体方式如下，

当强度应力比R小于等于0.3时，判定为无岩爆；R大于0.3且小于等于0.4时，判定为弱岩爆；R大于0.4时，结合应力集度η和强度应力R综合判定岩爆强度，当η-2R＜1.5或η-6.8R≥0.7或η/R≥8.6时，判定为弱岩爆，当η-2R≥1.5或η-6.8R＜0.7时，判定为中岩爆，当η-6.8R≥0.7或η/R＜8.6时，判定为强岩爆。

本发明引入应力集度的概念，在总结大量工程岩爆实例的基础上，探讨了岩爆与应力大小及应力分布的相关性关系，在刻画应力场扰动和岩爆强度方面将应力集度参数与强度应力比及岩爆等级相结合，开展了多参量表达式经验拟合，建立更为准确、合理的预测方法。本发明对于提高岩爆灾害的防控水平，降低人员、设备、工期的损失，具有重要的理论价值和应用前景。

具体来说，本发明具有如下技术特点和优点：

1、已有的基于强度理论的岩爆判据仅考虑围岩应力大小而未考虑围岩的应力分布，本发明引入了应力集度的概念，并提出其简化计算方法，结合大量工程实例，将工程得到的岩爆数据表示在由应力集度与强度应力比的二维平面内，开展了多参量表达式经验拟合，所建立的岩爆判据在岩爆预测准确率方面更高。

2、已有的岩爆判据考虑的主要因素主要集中于应力场和岩体力学特性，对于尺寸效应的影响并没有直接涉及，而尺寸效应一直是岩石力学界研究的热点，但缺乏有效的研究手段和计算工具，本判据可从定量的角度将岩爆和尺寸效结合起来。

3、本判据克服了传统强度应力比岩爆判据区间划分不统一的问题。

4、所建立的岩爆判据，应用简单、方便，可指导深埋隧洞工程的设计、施工。

附图说明

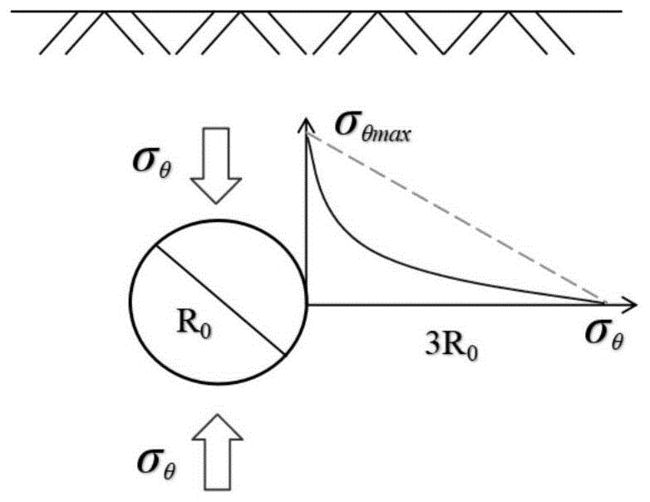
图1为本发明硐室开挖围岩一定深度范围内的切向应力分布形式。

图2为岩爆等级二维分布图。

图3为岩爆等级区域拟合图。

具体实施方式

下面结合附图对本发明技术方案进行详细说明，但是本发明的保护范围不局限于所述实施例。

一种考虑隧道围岩应力分布的强度应力比岩爆判据，具体实施步骤：

步骤1：如图1所示，为考虑应力分布，有必要对围岩应力扰动区做一系列的简化，由理论分析表明，由荷载释放引起的洞周介质应力和位移变化，3倍洞径之外小于5％，因此，假定三倍洞径处等于原岩应力。

由于围岩应力的变化率并非定值，因此，为方便表示二次应力在围岩扰动区的集中程度，简化为三角形，用直线变化率来表示应力分布。由此，引入应力集度参数：

η用来表示围岩切向的应力集度。式中，R0为开挖洞径，单位m，对于非圆形硐室可以采用当量方法来计算其洞径；σθ为开挖前隧道横截面最大初始应力，单位MPa；σθmax为洞壁切向应力最大值，单位MPa。

对于计算来说，我们忽略常数项，进一步简化为

步骤2：结合表1现场工程岩爆资料，计算得到各岩爆洞围岩强度应力比及应力集度η，将计算所得值表示为由强度比和应力集度所确定的二维平面中，如图2所示，以应力集度为x轴，强度应力比为y轴，结合工程现场的资料，得到应力集度、强度应力比及岩爆烈度的实测数据，表示在以应力集度与强度应力比所确定的二维平面内。

步骤3：用MATLAB编程对不同等级岩爆区间分界区域进行拟合，如图3所示，用拟合得到的分界线来建立综合考虑应力大小及应力分布的岩爆强度判据。具体如下：当强度应力比R小于等于0.3时，判定为无岩爆；R大于0.3且小于等于0.4时，判定为弱岩爆；R大于0.4时，结合应力集度η和强度应力R综合判定岩爆强度，当η-2R＜1.5或η-6.8R≥0.7或η/R≥8.6时，判定为弱岩爆，当η-2R≥1.5或η-6.8R＜0.7时，判定为中岩爆，当η-6.8R≥0.7或η/R＜8.6时，判定为强岩爆。

式中强度应力比R＝σθmax/σci，应力集度单位MPa·m-1，σci为围岩单轴抗压强度，单位MPa；其他参数意义同前述。

表1现场工程岩爆资料

参照上述方法，分别对其它地下工程样本的岩爆等级进行预测评价，得到其它样本的预测烈度，将样本的烈度等级预测结果与施工过程中的实际岩爆烈度等级相比较，如表2所示。

表2国内工程岩爆烈度的预测结果及实际结果

由表2的统计对比可以看出，传统的强度应力比岩爆判据的预测准确率仅为40％左右，其中，Russense和Hoek判据的准确率为35.3％，徐林生判据的准确率为41.2％，而本发明在考虑应力分布后的岩爆预测准确率可达到94.1％，说明本发明的技术方案实在岩爆预测方面的准确率更高。

[1]尚彦军，张镜剑，傅冰骏.应变型岩爆三要素分析及岩爆势表达[J]，岩石力学与工程学报，2013(8):1520-1527.

本发明所述技术方案，仅为本发明典型的实施方案，但本发明的保护范围并不局限于此，任何基于本发明的变化和替换，都应该涵盖在本发明的保护范围之内。因此，本发明的保护范围应以权力要求书的保护范围为准。