《Distance-IoU Loss：Faster and Better Learning for Bounding Box Regression》论文笔记
代码地址：DIoU
1. 概述
导读：这篇文章主要的贡献在边界框损失函数的优化上面，传统上使用 L n L_n Ln范数的损失，如smooth-L1或是其对应的改进balanced-L1，但是这些损失函数并不直接与检测框的质量相关。将检测框的质量作为回归的度量就引入IoU损失函数，为了弥补IoU损失函数在不相交的时候不可导的问题引入GIoU，但是GIoU也是存在收敛速度慢且回归不准确（GIoU在两个框相交时退化为IoU损失，且无法很好处理包含的情况）的问题。对此文章提出了将两个框的归一化距离作为损失度量的损失DIoU（Distance IoU），从而加快回归收敛与提升回归精度。在此之外，文章将框的IoU、中心点距离、以及框的宽高比例作为衡量预测与目标的要素，从而得到新的损失度量CIoU（Complete IoU）。另外，文章将提出的DIoU用作NMS的度量也会带来性能的提升。
边界框的损失函数从 l n l_n ln的范数损失到IoU损失的转换是直接将度量标准作为损失函数的过程，对应的IoU数学表达为：
I o U = ∣ B ∩ B g t ∣ ∣ B ∪ B g t ∣ IoU=\frac{|B\cap B^{gt}|}{|B\cup B^{gt}|} IoU=∣B∪Bgt∣∣B∩Bgt∣
则采用其作为边界框的回归损失，其定义为：
L I o U = 1 − ∣ B ∩ B g t ∣ ∣ B ∪ B g t ∣ L_{IoU}=1-\frac{|B\cap B^{gt}|}{|B\cup B^{gt}|} LIoU=1−∣B∪Bgt∣∣B∩Bgt∣
但是，上面的IoU-Loss存在边界框不相交的时候无法产生损失梯度的问题，对此的解决办法就再在外面套一个大框，从而得到的新的损失函数GIoU：
L G I o U = 1 − I o U + ∣ C − B ∪ B g t ∣ ∣ C ∣ L_{GIoU}=1-IoU+\frac{|C-B\cup B^{gt}|}{|C|} LGIoU=1−IoU+∣C∣∣C−B∪Bgt∣
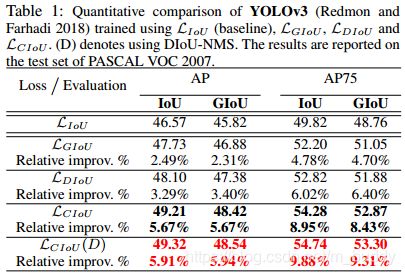
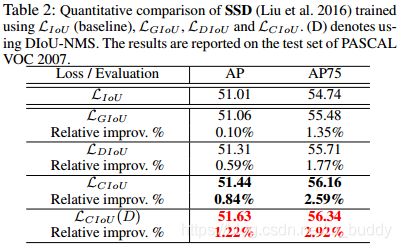
上述的损失函数解决了在不相交情况下不可导的问题，但是却存在收敛速度慢与性能不佳的问题，见下图是GIoU与文章提出的DIoU的比较：
上图中可以看出，GIoU在开始的时候需要将检测结果方法使其与目标框相交，之后才开始缩小检测结果与GT重合，这就带来了需要较多的迭代次数才能收敛问题，特别是对于水平与垂直框的情况下。此外，其在包含情况下检测框的性能无法有效度量，见下图所示
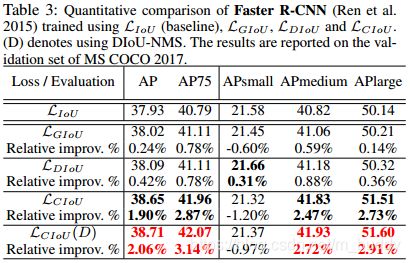
文章将上面涉及到的三种损失函数的错误画出进行对比：
2. 损失函数
文中将基于IoU的损失定义为如下形式：
L = 1 − I o U + R ( B , B g t ) L=1-IoU+R(B,B^{gt}) L=1−IoU+R(B,Bgt)
其中的计算函数 R R R就是文章中着重修正的地方。
2.1 DIoU损失
这里首先引出DIoU，后面的CIoU也是在这个基础上进行改进（增加长宽比例约束）得到的。这将额外的惩罚项由原有GIoU中的定义替换为了下面的形式：
R D I o U = ρ 2 ( b , b g t ) c 2 R_{DIoU}=\frac{\rho^2(b,b^{gt})}{c^2} RDIoU=c2ρ2(b,bgt)
其中， b , b g t b,b^{gt} b,bgt是 B , B g t B,B^{gt} B,Bgt的中心点， ρ ( ⋅ ) \rho(\cdot) ρ(⋅)是欧几里得距离， c c c是包含预测框与目标框的最小矩形的对角线长度（参考GIoU中C的定义）。上诉的几个参数在几何上的表示见下图所示：
则新的DIoU损失函数就被定义为：
L I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 L_IoU=1-IoU+\frac{\rho^2 (b,b^{gt})}{c^2} LIoU=1−IoU+c2ρ2(b,bgt)
DIoU与IoU、GIoU的关系：
- 1）DIoU依然是具有尺度不变性的；
- 2）与GIoU一样在两个框不相交的时候也能产生梯度，然后进行回归；
- 3）在检测框与预测框完全匹配的时候，他们之间的损失值为： L I o U = L G I o U = L D I o U = 0 L_{IoU}=L_{GIoU}=L_{DIoU}=0 LIoU=LGIoU=LDIoU=0，当两个框离得很远的时候： L G I o U = L D I o U → 2 L_{GIoU}=L_{DIoU} \rightarrow 2 LGIoU=LDIoU→2
DIoU损失相比IoU与GIoU的优势：
- 1）从图1与3可以看出DIoU收敛速度更快；
- 2）在两个框包含、水平与垂直方向的时候，DIoU仍能快速回归，而在这样的情况下GIoU退化为IoU损失；
2.2 CIoU损失
上面提出的DIoU是只考虑了框的位置关系，但是并没有考虑检测框与目标框的几何关系，因而这里还对框的几何关系做了约束，这里的约束是通过引入度量 v v v实现的，其定义为：
v = 4 π 2 ( a r c t a n w g t h g t − a r c t a n w h ) 2 v=\frac{4}{\pi^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})^2 v=π24(arctanhgtwgt−arctanhw)2
对于这个新引入的度量使用参数 α \alpha α进行调和，因而新的损失函数就可以定义为：
L C I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α v L_{CIoU}=1-IoU+\frac{\rho^2(b,b^{gt})}{c^2}+\alpha v LCIoU=1−IoU+c2ρ2(b,bgt)+αv
其中，参数 α = v ( 1 − I o U ) + v \alpha=\frac{v}{(1-IoU)+v} α=(1−IoU)+vv。
对于新引入的惩罚维度 v v v中的 w , h w,h w,h的梯度计算表达为：
∂ v ∂ w = 8 π 2 ( a r c t a n w g t h g t − a r c t a n w h ) ∗ h w 2 + h 2 \frac{\partial v}{\partial w}=\frac{8}{\pi^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})*\frac{h}{w^2+h^2} ∂w∂v=π28(arctanhgtwgt−arctanhw)∗w2+h2h
∂ v ∂ h = − 8 π 2 ( a r c t a n w g t h g t − a r c t a n w h ) ∗ w w 2 + h 2 \frac{\partial v}{\partial h}=-\frac{8}{\pi^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})*\frac{w}{w^2+h^2} ∂h∂v=−π28(arctanhgtwgt−arctanhw)∗w2+h2w
其中由于 w 2 + h 2 w^2+h^2 w2+h2的范围很小，作为被除数会导致较大的梯度，这样会导致网络不稳定，因而文中将最后一项设置为 1 w 2 + h 2 = 1 \frac{1}{w^2+h^2}=1 w2+h21=1
2.3 使用DIoU改进NMS
之前的NMS操作直接使用IoU剔除多余的检测框，在引入DIoU之后则新的剔除规则被描述为：
s i = { s i , I o U − R D I o U ( M , B i ) < ϵ 0 , I o U − R D I o U ( M , B i ) ≥ ϵ s_i = \begin{cases} s_i, & \text{$IoU-R_{DIoU}(M,B_i)\lt\epsilon$} \\ 0, & \text{$IoU-R_{DIoU}(M,B_i)\ge\epsilon$} \end{cases} si={si,0,IoU−RDIoU(M,Bi)<ϵIoU−RDIoU(M,Bi)≥ϵ
其中， s i s_i si是检测框分类置信度， ϵ \epsilon ϵ是NMS的阈值。
3. 实验结果
baseline为YOLO-V3
baseline为SSD
baseline为Faster RCNN
