经典算法系列之(三):七大查找——二分查找
活动地址:CSDN21天学习挑战赛
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。
一.什么是二分查找?
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
二.基本思想
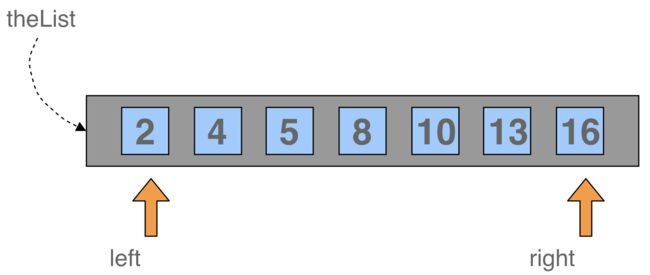
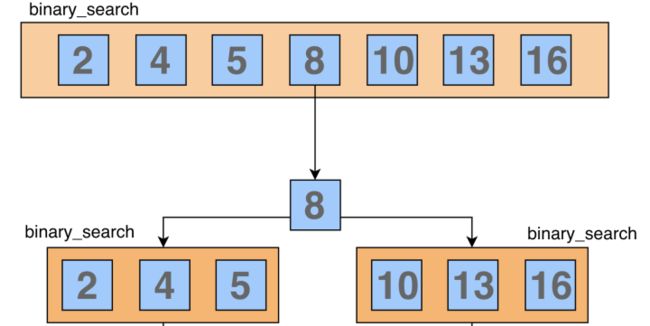
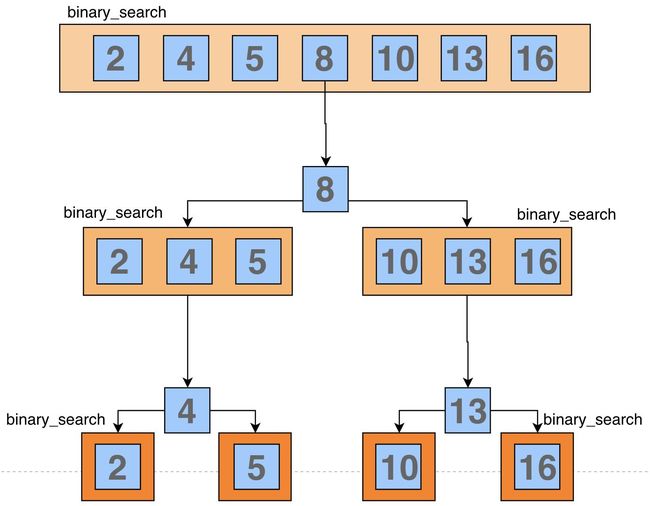
首先用要查找的关键字key与中间位置的结点的关键字相比较,这个中间结点把线性表分成了两个子表,若比较结果相等则查找完成;若不相等,再根据k与该中间节点关键字的的比较大小来去确定下一步查找哪个子表(如果我们把一个线性表想成是水平的,如果key值大于中间节点,则在右边的子表继续查找;如果key值小于中间值,则在左边的子表继续查找),这样递归下去,直到找到满足条件的节点或者该线性表中没有这样的节点。
图解:
1.
2.
3.
三.二分查找的优缺点
优点:
比较次数少,查找速度快,平均性能好。
缺点:
必须要求待查表为有序表(若为无序数组,分成两份查找没有意义,排序本身也要耗费时间);插入删除困难(曾删操作需要移动大量的节点)
四.时间以及空间复杂度
1.时间复杂度分析:
最坏的情况下:两种方式时间复杂度一样:O(log2 N)
最好情况下:O(1)
2.空间复杂度分析:
算法的空间复杂度并不是计算实际占用的空间,而是计算整个算法的辅助空间单元的个数
1.循环方式:
由于辅助空间是常数级别的所以:
空间复杂度是O(1);
2. 递归方式:
递归的次数和深度都是log2 N,每次所需要的辅助空间都是常数级别的:
空间复杂度:O(log2N )
五.二分查找的注意事项
1.while 中的循环条件:left < right 还是 left <= right
2.对于右侧边界的处理:right = middle 还是 right =middle-1对于以上细节的区分处理主要取决于查找区间的形式:左闭右闭区间 还是 左闭右开区间
3.间值mid的取法可能是学会二分法后,几乎是必遇的一个问题。很多人往往是用上述伪代码中的mid=(low+high)/2来取,这样的写法在low和high的值很大的时候就可能存在溢出的问题,像C,C++等,int、long这些都是有范围的,这样写轻则得不到结果,重则死循环程序崩溃,虽然这种情况在业务操作中极少出现,但还是建议用mid=low+(high-low)/2来取。
六.使用条件
因为二分查找需要方便定位查找的区域,所以其存储结构必须具有随机存取的特性,即该查找方式仅适用于线性表的顺序存储结构,不适用于链式存储结构,且元素要求按关键字或对象的某一属性有序排列。
六.代码实现:
流程
先判断为否为有顺序的表,然后想好是找位置还是找次数,最后判断使用递归还是非递归,记得确定好中值(mid),不要越界。
查找某数的位置(或存在性)
1.非递归
1 //返回"-1"表示为找到
2 //否则返回目标的下标(若有多个,只是其中一个)
3 int binary_searchs(int * arr, int x, int l, int r)
4 {
5 int lt = l, rt = r;
6 while (lt <= rt)
7 {
8 int mid = (lt + rt) >> 1;
9 if (arr[mid] == x) return mid;
10 else if (arr[mid] < x)
11 lt = mid + 1;
12 else
13 rt = mid - 1;
14 }
15 return -1;
16 }2.递归
int binary_searchs(int *arr, int target, int l, int r)
{
if (l > r) return -1;
int mid = (l + r) >> 1;
if (arr[mid] == target)
return mid;
else if (arr[mid] > target)
binary_search(arr, target, l, mid - 1);
else
binary_search(arr, target, mid + 1, r);
}
//返回"-1"表示为找到
//否则返回目标的下标(若有多个,只是其中一个)查找某数出现的次数
1.非递归
1 int binary_searchs(int *arr, int target,int l, int r)
2 {
3 int res = 0;
4 while (l <= r)
5 {
6 int mid = (l + r) >> 1;
7 if (arr[mid] == target)
8 {
9 if (l == r)
10 {
11 res++;
12 break;
13 }
14 for (int i = mid + 1; i <= r; i++)
15 if (arr[mid] == arr[i])
16 res++;
17 for (int i = mid - 1; i >= l; i--)
18 if (arr[mid] == arr[i])
19 res++;
20 res++;
21 break;
22 }
23 else if (arr[mid] < target)
24 l = mid + 1;
25 else if (arr[mid] > target)
26 r = mid - 1;
27 }
28 return res;
29 }2.递归
1 //返回target的出现次数
2 //返回0意味着不存在
3 int binary_search(int *arr, int target, int l, int r)
4 {
5 if (l > r) return 0;
6 int mid = (l + r) >> 1;
7 if (arr[mid] == target)
8 return 1 + binary_search(arr, target, l, mid - 1) + binary_search(arr, target, mid + 1, r);
9 else if (arr[mid] > target)
10 binary_search(arr, target, l, mid - 1);
11 else
12 binary_search(arr, target, mid + 1, r);
13 }