科学计算库 —— Numpy
Numpy
- 1 Numpy介绍
- 2 数组的属性
- 3 数组的操作
-
- 3.1 创建数组
- 3.2 数组的索引、切片
- 3.3 修改形状
- 3.4 修改类型
- 3.5 数组的去重
- 4 数组的运算
-
- 4.1 数组中运算
- 4.2 数组间运算
- 5 矩阵运算
1 Numpy介绍
Numpy(Numerical Python)是一个开源的Python科学计算库,用于快速处理任意维度的数组。
- Numpy数组是同质数组,即所有元素的数据类型必须相同
- Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务,使用Numpy比直接使用Python要简洁的多。
- Numpy使用
ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器。
import numpy as np
# 创建ndarray
score = np.array(
[[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])
print(score)
"""
array([[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])
"""
使用Python列表可以存储一维数组,通过列表的嵌套可以实现多维数组,那么为什么还需要使用Numpy的ndarray呢?
在这里我们通过一段代码运行来体会到ndarray的好处:
import random
import time
import numpy as np
a = []
for i in range(100000000):
a.append(random.random())
# 通过%time魔法方法, 查看当前行的代码运行一次所花费的时间
%time sum1=sum(a)
b=np.array(a)
%time sum2=np.sum(b)
"""
CPU times: user 852 ms, sys: 262 ms, total: 1.11 s
Wall time: 1.13 s
CPU times: user 133 ms, sys: 653 µs, total: 133 ms
Wall time: 134 ms
"""
机器学习的最大特点就是大量的数据运算,那么如果没有一个快速的解决方案,那可能现在python也在机器学习领域达不到好的效果。
ndarray为什么可以这么快?
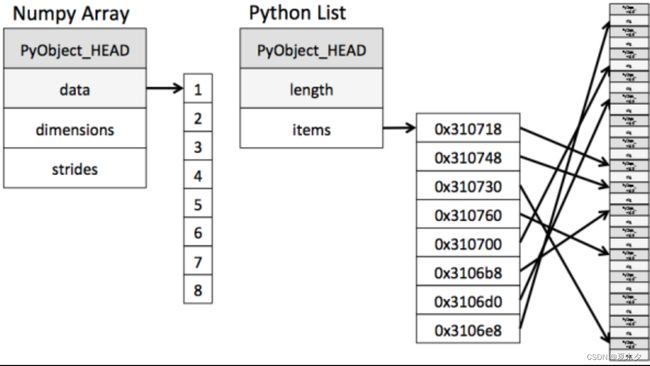
(1) 内存块风格
ndarray在存储数据的时候,数据与数据的地址都是连续的,这样就给使得批量操作数组元素时速度更快。这是因为ndarray中的所有元素的类型都是相同的,而Python列表中的元素类型是任意的,所以ndarray在存储元素时内存可以连续,而python原生list就只能通过寻址方式找到下一个元素,这虽然也导致了在通用性能方面Numpy的ndarray不及Python原生list,但在科学计算中,Numpy的ndarray就可以省掉很多循环语句,代码使用方面比Python原生list简单的多。
(2)ndarray支持并行化运算(向量化运算)
numpy内置了并行运算功能,当系统有多个核心时,做某种计算时,numpy会自动做并行计算
(3)效率远高于纯Python代码
Numpy底层使用C语言编写,内部解除了GIL(全局解释器锁),其对数组的操作速度不受Python解释器的限制,所以,其效率远高于纯Python代码。
2 数组的属性
import numpy as np
# 创建不同形状的数组
a = np.array([[1,2,3],[4,5,6]])
b = np.array([10,2,3,4])
c = np.array([[[1,2,3],[4,5,6]],[[1,2,3],[4,5,6]]])
# 分别打印出形状
print(a.shape) # (2, 3)
print(b.shape) # (4,)
print(c.shape) # (2, 2, 3)
改变数组的形状
a.shape=(3,2)
print(a)
"""
array([[1, 2],
[3, 4],
[5, 6]])
"""
改变数组的形状,前提是数组的个数要够
(2)数组的维度
print(a.ndim) # 2
print(b.ndim) # 1
print(c.ndim) # 3
(3)数组中的元素个数
print(a.size) # 6
print(b.size) # 4
print(c.size) # 12
(3)单个数组元素的大小(字节)
print(a.itemsize) # 4
print(b.itemsize) # 4
print(c.itemsize) # 4
(4)数组元素的类型
print(a.dtype) # dtype('int32')
3 数组的操作
3.1 创建数组
(1)生成0和1的数组
np.zeros(shape, dtype)和np.zeros_like(ndarray, dtype)np.ones(shape, dtype)和np.ones_like(ndarray, dtype)
>>> import numpy as np
>>> a = np.zeros(10)
>>> a
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
>>> b = np.ones_like(a,dtype="int64")
>>> b
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int64)
该生成数组的方式,元素类型默认为
float64
(2)从现有数组生成
>>> a = np.array([[1,2,3],[4,5,6]])
# 从现有的数组当中创建
>>> a1 = np.array(a)
# 相当于索引的形式,并没有真正的创建一个新的
>>> a2 = np.asarray(a)
# 改变数组a第一个元素的值
>>> a[0,0]=100
>>> a1
array([[1, 2, 3],
[4, 5, 6]])
>>> a2
array([[100, 2, 3],
[ 4, 5, 6]])
(3)生成随机数组
① 正态分布
正态分布基础
正态分布是一种概率分布。正态分布是具有两个参数μ和σ的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ是此随机变量的标准差,所以正态分布记作N(μ,σ )。

μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
方差:是在概率论和统计方差衡量一组数据时离散程度的度量

其中M为平均值,n为数据总个数,σ 为标准差,σ ^2可以理解一个整体为方差
方差越小,数据越稳定,曲线越高瘦
正态分布创建方式
-
np.random.randn(d0, d1, …, dn)从标准正态分布中返回一个或多个样本值 -
np.random.standard_normal(size=None)返回指定形状的标准正态分布的数组 -
np.random.normal(loc=0.0, scale=1.0, size=None)正态分布- loc:float,此概率分布的均值
- scale:float,此概率分布的标准差
- size:输出样本数目,为
int或tuple类型
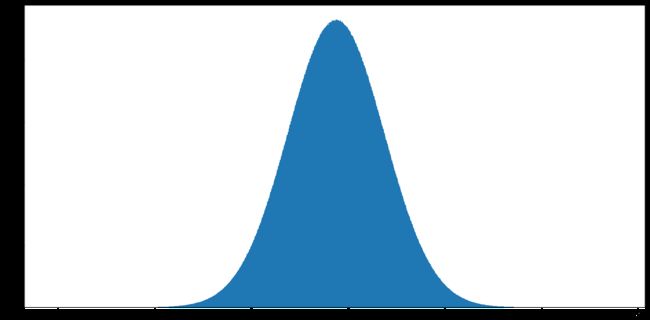
import numpy as np
import matplotlib.pyplot as plt
# 生成均匀分布的随机数
x1 = np.random.normal(1.75, 1, 100000000) # 输出样本为int整型
# 画图看分布状况
# 1)创建画布
plt.figure(figsize=(20, 10), dpi=100)
# 2)绘制直方图
plt.hist(x1, 1000) # 1000组
# 3)显示图像
plt.show()
# 创建符合正态分布的4只股票5天的涨跌幅数据
>>> stock_change = np.random.normal(0, 1, (4, 5)) # 输出样本为数组
>>> stock_change
array([[ 0.68999755, -1.6207249 , 0.98207475, -0.57027007, 0.22092417],
[ 0.56208104, 2.04490099, -0.3562128 , 1.04113141, -0.28646248],
[ 0.4141092 , -0.42319679, 0.80749131, 0.16229998, 0.98407121],
[-0.8845948 , -0.99775534, -1.11351838, 0.775468 , -0.91367774]])
② 均匀分布
np.random.rand(d0, d1, ..., dn)返回[0.0,1.0)内的一组均匀分布的数。np.random.uniform(low=0.0, high=1.0, size=None)从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high.
参数介绍:
- low: 采样下界,float类型,默认值为0;
- high: 采样上界,float类型,默认值为1;
- size: 输出样本数目,为int或元组(tuple)类型,例如,size=(m,n,k), 则输出mnk个样本,缺省时输出1个值。
返回值:ndarray类型,其形状和参数size中描述一致。
np.random.randint(low, high=None, size=None, dtype='l')从一个均匀分布中随机采样,生成一个整数或N维整数数组,
取数范围:若high不为None时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数。
import numpy as np
import matplotlib.pyplot as plt
# 生成均匀分布的随机数
x2 = np.random.uniform(-1, 1, 100000000)
# 画图看分布状况
# 1)创建画布
plt.figure(figsize=(10, 10), dpi=100)
# 2)绘制直方图
plt.hist(x=x2, bins=1000) # x代表要使用的数据,bins表示要划分区间数
# 3)显示图像
plt.show()
(4)生成固定范围的数组
① np.linspace (start, stop, num, endpoint)创建一个指定数量的等差数列
参数:
- start:序列的起始值
- stop:序列的终止值
- num:要生成的等间隔样例数量,默认为50
- endpoint:序列中是否包含stop值,默认为ture
# 生成等间隔的数组
>>> np.linspace(0, 100, 11)
array([ 0., 10., 20., 30., 40., 50., 60., 70., 80., 90., 100.])
② np.logspace(start,stop, num) 创建等比数列(默认以10为底)
参数:
- num:要生成的等比数列数量,默认为50
# 生成10^x
>>> np.logspace(0, 2, 3)
array([ 1., 10., 100.])
③ np.arange(start,stop, step, dtype)创建一个指定步长的等差数组
参数
- step:步长,默认值为1
>>> np.arange(10, 30, 2)
array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28])
3.2 数组的索引、切片
二维数组索引方式:
>>> stock_change[0,:3]
array([ 0.68999755, -1.6207249 , 0.98207475])
三维数组索引方式:
>>> a1 = np.array([ [[1,2,3],[4,5,6]], [[12,3,34],[5,6,7]]])
>>> a1
array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[12, 3, 34],
[ 5, 6, 7]]])
# 索引、切片
>>> a1[0, 0, 1] # 2
3.3 修改形状
(1)ndarray.reshape(shape, order)
- 返回一个具有相同数据域,但shape不一样的视图
- 行、列不进行互换
# 在转换形状的时候,一定要注意数组的元素匹配
>>> stock_change.reshape([5, 4])
array([[ 0.68999755, -1.6207249 , 0.98207475, -0.57027007],
[ 0.22092417, 0.56208104, 2.04490099, -0.3562128 ],
[ 1.04113141, -0.28646248, 0.4141092 , -0.42319679],
[ 0.80749131, 0.16229998, 0.98407121, -0.8845948 ],
[-0.99775534, -1.11351838, 0.775468 , -0.91367774]])
>>> stock_change.reshape([-1,10]) # 数组的形状被修改为: (2, 10), -1: 表示通过待计算
array([[ 0.68999755, -1.6207249 , 0.98207475, -0.57027007, 0.22092417,
0.56208104, 2.04490099, -0.3562128 , 1.04113141, -0.28646248],
[ 0.4141092 , -0.42319679, 0.80749131, 0.16229998, 0.98407121,
-0.8845948 , -0.99775534, -1.11351838, 0.775468 , -0.91367774]])
注意:stock_change自身的形状并没有改变
(2)ndarray.resize(new_shape)
- 修改数组本身的形状(需要保持元素个数前后相同)
- 行、列不进行互换
>>> stock_change.resize([5, 4])
>>> stock_change
array([[ 0.12023882, -1.01334009, -0.96260835, 1.35681109],
[-2.338144 , -0.03747404, -0.41182821, -0.30680214],
[ 0.9536047 , -1.17634426, -0.16533181, -0.14403163],
[-0.14038189, 0.72956787, -1.12202168, 1.03254905],
[ 1.29231532, -0.42151677, 0.35123619, 0.24053709]])
# 查看修改后结果
>>> stock_change.shape # (5, 4)
(3)ndarray.T
- 数组的转置
- 将数组的行、列进行互换
>>> stock_change.T.shape # (4, 5)
3.4 修改类型
(1)ndarray.astype(type)返回修改了类型之后的数组
>>> stock_change.dtype # dtype('float64')
>>> stock_change.astype(np.int64)
>>> stock_change.dtype # dtype('float64')
(2)ndarray.tostring([order])或者ndarray.tobytes([order])
>>> arr = np.array([[[1, 2, 3], [4, 5, 6]], [[12, 3, 34], [5, 6, 7]]])
>>> arr.tostring()
b'\x01\x00\x00\x00\x02\x00\x00\x00\x03\x00\x00\x00\x04\x00\x00\x00\x05\x00\x00\x00\x06\x00\x00\x00\x0c\x00\x00\x00\x03\x00\x00\x00"\x00\x00\x00\x05\x00\x00\x00\x06\x00\x00\x00\x07\x00\x00\x00'
3.5 数组的去重
>>> import numpy as np
>>> temp = np.array([[1, 2, 3, 4],[3, 4, 5, 6]])
>>> temp
array([[1, 2, 3, 4],
[3, 4, 5, 6]])
>>> np.unique(temp)
array([1, 2, 3, 4, 5, 6])
4 数组的运算
4.1 数组中运算
(1)逻辑运算
# 生成10名同学,5门功课的数据
>>> score = np.random.randint(40, 100, (10, 5))
# 取出最后4名同学的成绩,用于逻辑判断
>>> test_score = score[6:, 0:5]
# 逻辑判断, 如果成绩大于60就标记为True 否则为False
>>> test_score > 60
array([[False, False, True, True, True],
[ True, True, True, True, True],
[ True, False, True, False, True],
[ True, True, False, False, True]])
# BOOL赋值, 将满足条件的设置为指定的值-布尔索引
>>> test_score[test_score > 60] = 1
>>> test_score
array([[46, 54, 1, 1, 1],
[ 1, 1, 1, 1, 1],
[ 1, 51, 1, 45, 1],
[ 1, 1, 49, 43, 1]])
(2)统计运算
在数据挖掘/机器学习领域,统计指标的值也是我们分析问题的一种方式。常用的指标如下:
min(a, axis)返回数组的最小值或沿轴的最小值。max(a, axis])返回数组的最大值或沿轴的最大值median(a, axis)沿指定轴计算中值mean(a, axis, dtype)沿指定轴计算算术平均值std(a, axis, dtype)计算沿指定轴的标准差var(a, axis, dtype)计算沿指定轴的方差np.argmax(axis)最大元素对应的下标np.argmin(axis)最小元素对应的下标
axis=0代表跨行,即一列, axis=1代表跨列,即一行
# 接下来对于前四名学生,进行一些统计运算
# 指定列 去统计
>>> temp = score[:4, 0:5]
>>> temp
array([[84, 63, 47, 88, 55],
[75, 70, 69, 83, 62],
[74, 50, 69, 73, 43],
[58, 54, 86, 97, 69]])
# 接下来对于前四名学生,进行一些统计运算
# 指定列 去统计
>>> temp = score[:4, 0:5]
>>> print("前四名学生,各科成绩的最大分:{}".format(np.max(temp, axis=0)))
>>> print("前四名学生,各科成绩的最小分:{}".format(np.min(temp, axis=0)))
>>> print("前四名学生,各科成绩波动情况:{}".format(np.std(temp, axis=0)))
>>> print("前四名学生,各科成绩的平均分:{}".format(np.mean(temp, axis=0)))
>>> print("前四名学生,各科成绩最高分对应的学生下标:{}".format(np.argmax(temp, axis=0)))
前四名学生,各科成绩的最大分:[84 70 86 97 69]
前四名学生,各科成绩的最小分:[58 50 47 73 43]
前四名学生,各科成绩波动情况:[ 9.3641604 7.79021823 13.8451255 8.6710726 9.60143218]
前四名学生,各科成绩的平均分:[72.75 59.25 67.75 85.25 57.25]
前四名学生,各科成绩最高分对应的学生下标:[0 1 3 3 3]
(3)通用判断函数
① np.all()
# 判断前两名同学的成绩[0:2, :]是否全及格
>>> np.all(score[0:2, :] > 60)
False
② np.any()
# 判断前两名同学的成绩[0:2, :]是否有大于90分的
>>> np.any(score[0:2, :] > 80)
True
(4)三元运算符
通过使用np.where能够进行更加复杂的运算
# 判断前四名学生,前四门课程中,成绩中大于60的置为1,否则为0
temp = score[:4, :4]
np.where(temp > 60, 1, 0)
复合逻辑需要结合np.logical_and和np.logical_or使用
# 判断前四名学生,前四门课程中,成绩中大于60且小于90的换为1,否则为0
np.where(np.logical_and(temp > 60, temp < 90), 1, 0)
# 判断前四名学生,前四门课程中,成绩中大于90或小于60的换为1,否则为0
np.where(np.logical_or(temp > 90, temp < 60), 1, 0)
4.2 数组间运算
(1)数组与数
>>> arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
>>> arr
array([[1, 2, 3, 2, 1, 4],
[5, 6, 1, 2, 3, 1]])
>>> arr + 1
array([[2, 3, 4, 3, 2, 5],
[6, 7, 2, 3, 4, 2]])
>>> arr / 2
array([[0.5, 1. , 1.5, 1. , 0.5, 2. ],
[2.5, 3. , 0.5, 1. , 1.5, 0.5]])
# 可以对比python列表的运算,看出区别
>>> a = [1, 2, 3, 4, 5]
>>> a * 3
[1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5]
(2)数组与数组
>>> arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
>>> arr2 = np.array([[1, 2, 3, 4], [3, 4, 5, 6]])
>>> arr1+arr2 # 不可以进行运算
广播机制
数组在进行矢量化运算时,要求数组的形状是相等的。当形状不相等的数组执行算术运算的时候,就会出现广播机制,该机制会对数组进行扩展,使数组的shape属性值一样,这样,就可以进行矢量化运算了。下面通过一个例子进行说明:
>>> arr1 = np.array([[0],[1],[2],[3]])
>>> arr1.shape
(4, 1)
>>> arr2 = np.array([1,2,3])
>>> arr2.shape
(3,)
>>> arr1+arr2
array([[1, 2, 3],
[2, 3, 4],
[3, 4, 5],
[4, 5, 6]])
广播机制实现了两个或两个以上数组的运算,即使这些数组的shape不是完全相同的,只需要满足如下任意一个条件即可。
- 数组的某一维度等长
- 其中一个数组的某一维度为1
>>> arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
>>> arr1
array([[1, 2, 3, 2, 1, 4],
[5, 6, 1, 2, 3, 1]])
>>> arr1.shape
(2, 6)
>>> arr2 = np.array([[1], [3]])
>>> arr2
array([[1],
[3]])
>>> arr.shape
(2, 1)
>>> arr1+arr2
array([[2, 3, 4, 3, 2, 5],
[8, 9, 4, 5, 6, 4]])
5 矩阵运算
>>> a = np.array([[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]])
>>> b = np.array([[0.7], [0.3]])
>>> np.matmul(a, b)
array([[81.8],
[81.4],
[82.9],
[90. ],
[84.8],
[84.4],
[78.6],
[92.6]])
>>> np.dot(a,b)
array([[81.8],
[81.4],
[82.9],
[90. ],
[84.8],
[84.4],
[78.6],
[92.6]])
注意:二者都是矩阵乘法。
np.matmul中禁止矩阵与标量的乘法。 在矢量乘矢量的內积运算中,np.matmul与np.dot没有区别。