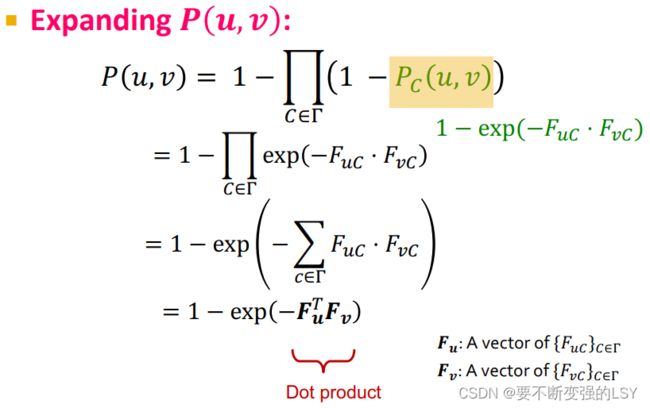【从零开始】CS224W-图机器学习 学习笔记4.2:Community Structure in Networks(2)——BigCLAM算法
课程主页:CS224W | Home
课程视频链接:【斯坦福】CS224W:图机器学习( 中英字幕 | 2019秋)
文章目录
1 前言
2 重叠社团发现算法——BigCLAM算法
2.1 算法主要步骤
2.2 AGM模型(Community-Affiliation Graph Model)
2.3 算法思路:通过拟合图来发现社团
2.4 BigCLAM算法
3 总结
4 参考资料
1 前言
上一节介绍了模块度![]() 和Louvain算法,Louvain算法适用于不重叠的(Non-overlapping)社团发现,但是我们现实生活中很多社团其实是存在重叠的(Overlapping),反映在邻接矩阵上如下图:
和Louvain算法,Louvain算法适用于不重叠的(Non-overlapping)社团发现,但是我们现实生活中很多社团其实是存在重叠的(Overlapping),反映在邻接矩阵上如下图:
下面就介绍另一种重叠的社团发现算法——BigCLAM算法。
2 重叠社团发现算法——BigCLAM算法
2.1 算法主要步骤
- 第一步:定义一个基于节点-社团隶属关系的生成图的模型(Community Affiliation Graph Model (AGM))
- 第二步:给定一个图G,假设其由AGM模型生成,迭代找到能生成最接近图G的AGM模型
- 通过这种方式,我们就能发现图中的社团。
2.2 AGM模型(Community-Affiliation Graph Model)
通过节点-社区隶属关系(左图)生成相应的网络(右图)。
参数:节点V,社区C ,成员关系M,每个社区C有个概率![]() (表示社区c内的节点之间生成边的概率)
(表示社区c内的节点之间生成边的概率)
这样,对与属于多个社团的节点对,其相连概率就是:
对于该公式进行分类讨论,可得到:
- 当两个节点在同一个社区c时,即只有一种成员关系
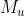 时,节点之间以
时,节点之间以 的概率进行相连:
的概率进行相连:
- 当两个节点不属于同一个社区时,节点之间没有边进行相连:
![]()
注:这看起来并不合理,所以会假设有一个“epsilon”社区,所有节点都属于它,但是epsilon会很小。这样,任意两个节点之间都会有一个很小的概率能建立连接,即![]()
- 当两个节点属于两个社区时,即存在两种不同成员关系
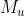 和
和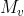 时:
时:
注:因为![]() 和
和![]() 都小于1,所以
都小于1,所以![]() 一定大于
一定大于![]() 和
和![]() 。从社交网络上理解,就是两个人所处的共同圈子越多,他们认识的可能性就越大。
。从社交网络上理解,就是两个人所处的共同圈子越多,他们认识的可能性就越大。
AMG模型是在重叠社区挖掘的时候引入的,但并不意味着AMG模型只能生成有重叠社区的网络。事实上,其非常灵活,可以生成不同类型的社团结构:
2.3 算法思路:通过拟合图来发现社团
社团发现的过程其实正是构建上述节点-社团隶属关系的二分图模型的过程,即上文“用AMG模型生成图”过程的逆过程。也就是说,给定一个图G,我们需要找到一个二分图模型F,且得到相关的参数。
解决这个问题的思路关键在于:已知真实图![]() ,找到模型
,找到模型![]() ,使得由
,使得由![]() 生成的图和真实的图
生成的图和真实的图![]() 尽量接近,也就是使得
尽量接近,也就是使得![]() 关于
关于![]() 的条件概率最大,也就是极大似然估计(Maximum Likelihood Estimation,MLE)。
的条件概率最大,也就是极大似然估计(Maximum Likelihood Estimation,MLE)。
那么,我们就需要找到一个计算条件概率![]() 的高效的方法,并遍历模型
的高效的方法,并遍历模型![]() ,其中条件概率
,其中条件概率 ![]() 最大的模型
最大的模型![]() 就是我们需要的社团结构。
就是我们需要的社团结构。
在AGM算法中,![]() 表示的是两个结点之间产生连边的概率。在真实网络G中,两点相连的时候
表示的是两个结点之间产生连边的概率。在真实网络G中,两点相连的时候![]() ,两点不相连的时候
,两点不相连的时候 ![]() 。在模型F中,为了让它更贴合真实网络G,我们希望相连的两点之间的概率尽可能大,不相连的两点之间的概率尽可能小。这样就得到我们的目标函数:
。在模型F中,为了让它更贴合真实网络G,我们希望相连的两点之间的概率尽可能大,不相连的两点之间的概率尽可能小。这样就得到我们的目标函数:
有边就乘以产生连边的概率![]() ,没有边乘以不产生连边的概率,即
,没有边乘以不产生连边的概率,即![]() ,不断更新F的参数,就使得
,不断更新F的参数,就使得![]() 的增大,使F模型生成的G越来越接近给定的真实的G。
的增大,使F模型生成的G越来越接近给定的真实的G。
而BigCLAM算法的思想也是一样的,但是在概率![]() 和目标函数的形式上做了改进,增加了成员关系M上的权重。
和目标函数的形式上做了改进,增加了成员关系M上的权重。
2.4 BigCLAM算法
和AGM模型相比,BigCLAM模型在AGM的基础上进行了松弛(Relax),即增添了成员关系强度。
定义一个参量![]() ,表示节点u属于社团A的成员关系的强度。对于AGM的二部图,每个节点u和社团之间的成员关系M转变成一个向量
,表示节点u属于社团A的成员关系的强度。对于AGM的二部图,每个节点u和社团之间的成员关系M转变成一个向量![]() 。向量的维度是社团的数量,比如有3个社团就是3维。 u属于的社团对应的位置就是1,不属于的社团就是0。
。向量的维度是社团的数量,比如有3个社团就是3维。 u属于的社团对应的位置就是1,不属于的社团就是0。
由此,我们就可以重新定义社团c内节点间的连接概率![]() :
:
![]()
在这个式子中,因为![]() ,所以有
,所以有![]() ,使得
,使得![]() ,另外,在这个式子中可能出现的两种特殊情况:
,另外,在这个式子中可能出现的两种特殊情况:
得到新的![]() 后,我们就可以进一步扩展
后,我们就可以进一步扩展![]() :(连乘放到幂里变成连加)
:(连乘放到幂里变成连加)
注:因为社团的数量可能会很多,所以这里用![]() 表示所有社团的集合。
表示所有社团的集合。
再把得到的![]() 带入到
带入到![]() 公式中,得到:
公式中,得到:
再将此结果取对数,得到我们的目标函数![]() :
:
使用梯度上升的方法来优化目标函数的参数,使log-likelihood提升:(下面这个公式的推导太复杂了,我也没推出来,先放一个Jure的推导结果)
注: 在Jure的课件里,F还可以通过训练一个GNN模型来获得,这就是Neural Overlapping Community Detection (NOCD)的key idea,但是因为时间关系,Jure没有继续介绍。先Mark一下,等学完GNN再回来补充吧!
当我们找到了F,就可以生成想要的重叠社团,进而完成了我们的社区发现任务。
3 总结
BigCLAM定义了一个模型,可生成重叠社团结构的网络。给定一个图,BigCLAM的参数(每个节点的成员关系强度)可以通过最大化对数似然估计得到。
4 参考资料
http://snap.stanford.edu/class/cs224w-2019/slides/04-communities.pdf
社区发现算法——BigCLAM 算法_东方小虾米的博客-CSDN博客_bigclam
cs224w 图神经网络 学习笔记(五)Community Structure in Networks_喵木木的博客-CSDN博客