神经网络分类
活动地址:CSDN21天学习挑战赛
概念
感知机
| x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | Y |
|---|---|---|---|
| 1 | 0 | 0 | -1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | -1 |
| 0 | 1 | 0 | -1 |
| 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | -1 |
感知机
- 输入结点
- 输入结点做一个线性变化
- 把线性变化的值做一个符号函数
- 输出到输出结点
eg
y ^ { 1 , 0.3 x 1 + 0.3 x 2 + 0.3 x 3 − 0.4 > 0 − 1 , 0.3 x 1 + 0.3 x 2 + 0.3 x 3 − 0.4 < 0 \hat{y} \begin{cases} 1,\,\,0.3x_1+0.3x_2+0.3x_3-0.4>0\\ -1,\,\,0.3x_1+0.3x_2+0.3x_3-0.4<0 \end{cases} y^{1,0.3x1+0.3x2+0.3x3−0.4>0−1,0.3x1+0.3x2+0.3x3−0.4<0
- 感知机能够通过有限次训练就能学会正确的行为
- 感知机无法执行异或问题
多层感知机
用于解决感知机无法执行异或问题
即用两计算层感知器解决异或问题
| x 1 x_1 x1 | x 2 x_2 x2 | y 1 y_1 y1 | y 2 y_2 y2 | o |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
- 第一层感知机,将(1,0)作为一类,其它作为一类分开,得到第一层感知机结果 y 1 y_1 y1
- 第二层感知机,将(0,1)作为一类,其他作为一类分开,得到第二层感知机结果 y 2 y_2 y2
- 第三层感知机的输入,是前两层感知机的输出,三个点(1,1)(1,0)(0,1),很容易找到一条直线将他们分开,得到的输出就能解决异或问题
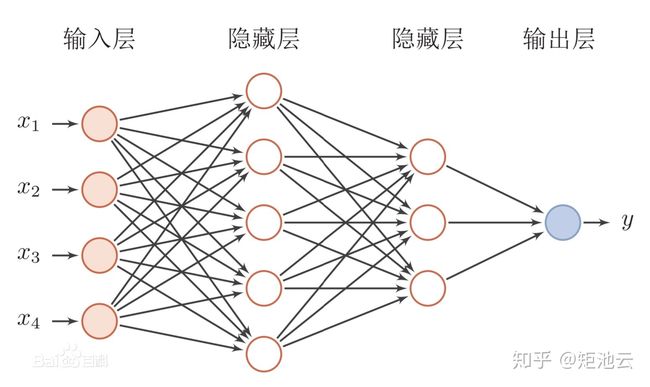
多层人工神经网络
误差反向传播(BP)网络
- 我们得到 o 1 o 2 . . . o n o_1\,\,o_2...o_n o1o2...on的预测值,预测值与真实值存在误差,这部分误差从上再往下进行传播
BP网络模型
-
激活函数
- 必须处处可导
- 一般使用S型函数——sigmoid函数
-
使用S型激活函数是BP网络输入与输出关系
-
输入
n e t = x 1 w 1 + x 2 w 2 + . . . + x n w n net=x_1w_1+x_2w_2+...+x_nw_n net=x1w1+x2w2+...+xnwn -
输出
y = f ( n e t ) = 1 1 + e − n e t y=f(net)=\frac{1}{1+e^{-net}} y=f(net)=1+e−net1
-
后向传播算法理论支撑
-
超参数
∙ 激活函数: S i g m o i d ∙ 损失函数:均方差损失——计算误差 B a t c h s i z e : 1 \bullet 激活函数:Sigmoid\\ \bullet 损失函数:均方差损失——计算误差\\ Batch\,\,\,size:1 ∙激活函数:Sigmoid∙损失函数:均方差损失——计算误差Batchsize:1 -
训练的参数
W e i g h t s ω → , B i a s b → 权值和偏置项 Weights\,\overrightarrow{\omega},Bias\,\overrightarrow{b}\\ 权值和偏置项 Weightsω,Biasb权值和偏置项 -
最小化
E = 1 2 ∑ j = 1 n ( y ^ j − y j ) 2 目的——均方误差尽可能的小 E=\frac{1}{2}\sum_{j=1}^n(\hat y_j-y_j)^2\\ 目的——均方误差尽可能的小 E=21j=1∑n(y^j−yj)2目的——均方误差尽可能的小
D = { ( x 1 → , y 1 → ) , ( x 2 → , y 2 → ) , . . . , ( x n → , y n → ) } , x → ∈ R 3 , y → ∈ R 3 D=\{(\overrightarrow{x_1},\overrightarrow{y_1}),(\overrightarrow{x_2},\overrightarrow{y_2}),...,(\overrightarrow{x_n},\overrightarrow{y_n}) \},\overrightarrow{x}\in R^3,\overrightarrow{y}\in R^3\\ D={(x1,y1),(x2,y2),...,(xn,yn)},x∈R3,y∈R3
——训练集
如何学习权值和偏置项
——梯度下降法
反复进行迭代学习,找到较优的权值和偏置项
激活函数
- 激活函数可以是多种函数
采用梯度下降法
即当前结果 = 上一次迭代结果 − 学习率 ∗ 梯度 θ 0 ← θ 0 − η ∂ f ∂ θ 0 即当前结果=上一次迭代结果-学习率*梯度\\ \theta_0\leftarrow\theta_0-\eta\frac{\partial f}{\partial \theta_0} 即当前结果=上一次迭代结果−学习率∗梯度θ0←θ0−η∂θ0∂f
-
第一种,线性激活函数
一般不使用,因为线性激活函数的梯度为0,则没有办法调整权值
-
Sigmoid函数
-
双面正切函数
-
符号函数
为了解决梯度消失的问题,我们通常补充使用线性整流函数 R e L U ReLU ReLU
f ( x ) = max ( 0 , x ) f ′ ( x ) = I ( x > 0 ) f(x)=\max(0,x)\\ f'(x)=I(x>0) f(x)=max(0,x)f′(x)=I(x>0)
- 解决了部分梯度消失的问题,而且梯度是常数,其权值可以根据这个常数进行调整
- 如果输入是负值,则导致梯度为0
当梯度为0,无法再调整权值时,我们称其为导致了神经元的死亡,我们通常设置一个较小的学习率来解决神经元的死亡
后向传播算法步骤
-
初始化权重
- 循环以下两步,直到满足条件
-
向前传播输入
- 在每个结点加权求和,再代入激活函数
y ^ = s i g n ( ∑ i w i j x i − t j ) \hat{y}=sign(\sum_iw_{ij}x_i-t_j) y^=sign(i∑wijxi−tj)
- 在每个结点加权求和,再代入激活函数
-
向后传播误差
E r r j = O j ( 1 − O j ) ( T j − O j ) E r r j = O j ( 1 − O j ) ∑ k E r r k w j k w i j = w i j + λ E r r j y i t j = t j + λ E r r j T j : 真实的输出 O j : 预测的输出 ∑ k E r r k w j k : 反向传播过来的误差 ∗ 对应权值 λ : 学习率 Err_j=O_j(1-O_j)(T_j-O_j)\\ Err_j=O_j(1-O_j)\sum_kErr_kw_{jk}\\ w_{ij}=w_{ij}+\lambda Err_jy_i\\ t_j=t_j+\lambda Err_j\\ T_j:真实的输出\\ O_j:预测的输出\\ \sum_kErr_kw_{jk}:反向传播过来的误差*对应权值\\ \lambda:学习率 Errj=Oj(1−Oj)(Tj−Oj)Errj=Oj(1−Oj)k∑Errkwjkwij=wij+λErrjyitj=tj+λErrjTj:真实的输出Oj:预测的输出k∑Errkwjk:反向传播过来的误差∗对应权值λ:学习率
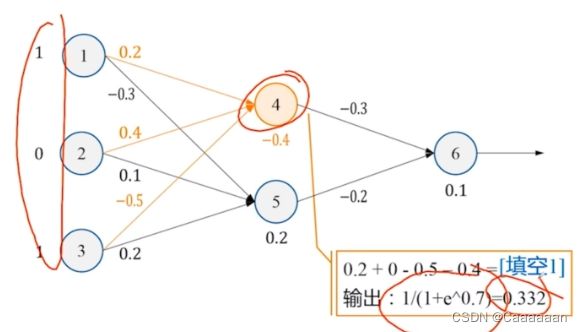
- 边上的值为权值,点下的值为偏置项
——正向传播
——误差反向传播过程
传播到4和5的时候,我们计算出4和5的误差之后,开始调整权值和偏置值
学习率:
- 学习率过大时,一步走的步子大,可以很快到达收敛点,但这个收敛点不一定是最优的收敛点,可能会在最优收敛点来回进行一个徘徊
- 学习率过小,步子很小,需要很多次的迭代次数,才能到达收敛点
得到新的权值和偏置值时,再进行一次正向传播和反向传播
直到误差小到一定程度,或者迭代次数达到阈值
注意事项
-
初始值选择
- 权值向量以及阈值的初始值应设定在一均匀分布的小范围内
- 初始值不能为零,否则性能曲面会趋于鞍点
- 初始值不能太大,否则会远离优化点,导致性能曲面平坦,学习率很慢
-
训练样本输入次序
- 不同,也会造成不一样的学习结果
- 在每一次的学习循环中,输入向量输入网络的次序应使其不同
-
BP算法的学习过程的终止条件
- 权值向量的梯度<给定值
- 均方误差值<给定误差容限值
- 若其推广能力达到目标则予中止
- 可以结合上述各种方式
-
普适近似,精度较多
-
噪声敏感
-
训练耗时,分类较快
编程实践
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd
data_url="diabetes.csv"
df=pd.read_csv(data_url)
X=df.iloc[:,0:8]
y=df.iloc[:,8]
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)
clf=MLPClassifier(solver='sgd',alpha=1e-5,hidden_layer_sizes=(5,2),random_state=1)
clf.fit(X_train,y_train)
参数说明
-
hidden_layer_sizes :例如hidden_layer_sizes=(50, 50),表示有两层隐藏层,第一层隐藏层有50个神经元,第二层也有50个神经元。
-
activation :激活函数,{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu
-
identity:f(x) = x
-
logistic:其实就是sigmod,f(x) = 1 / (1 + exp(-x)).
-
tanh:f(x) = tanh(x).
-
relu:f(x) = max(0, x)
- solver: {‘lbfgs’, ‘sgd’, ‘adam’}, 默认adam,用来优化权重
-
lbfgs:quasi-Newton方法的优化器
-
sgd:随机梯度下降
-
adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器
注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
-
alpha :float,可选的,默认0.0001,正则化项参数
-
batch_size : int , 可选的,默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples),如果solver是’lbfgs’,分类器将不使用minibatch
-
learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
-
‘constant’: 有’learning_rate_init’给定的恒定学习率
-
‘incscaling’:随着时间t使用’power_t’的逆标度指数不断降低学习率learning_rate_ ,effective_learning_rate = learning_rate_init / pow(t, power_t)
-
‘adaptive’:只要训练损耗在下降,就保持学习率为’learning_rate_init’不变,当连续两次不能降低训练损耗或验证分数停止升高至少tol时,将当前学习率除以5.
-
power_t: double, 可选, default 0.5,只有solver=’sgd’时使用,是逆扩展学习率的指数.当learning_rate=’invscaling’,用来更新有效学习率。
-
max_iter: int,可选,默认200,最大迭代次数。
-
random_state:int 或RandomState,可选,默认None,随机数生成器的状态或种子。
-
shuffle: bool,可选,默认True,只有当solver=’sgd’或者‘adam’时使用,判断是否在每次迭代时对样本进行清洗。
-
tol:float, 可选,默认1e-4,优化的容忍度
-
learning_rate_int:double,可选,默认0.001,初始学习率,控制更新权重的补偿,只有当solver=’sgd’ 或’adam’时使用。
-
verbose : bool, 可选, 默认False,是否将过程打印到stdout
-
warm_start : bool, 可选, 默认False,当设置成True,使用之前的解决方法作为初始拟合,否则释放之前的解决方法。
-
momentum : float, 默认 0.9,动量梯度下降更新,设置的范围应该0.0-1.0. 只有solver=’sgd’时使用.
-
nesterovs_momentum : boolean, 默认True, Whether to use Nesterov’s momentum. 只有solver=’sgd’并且momentum > 0使用.
-
early_stopping : bool, 默认False,只有solver=’sgd’或者’adam’时有效,判断当验证效果不再改善的时候是否终止训练,当为True时,自动选出10%的训练数据用于验证并在两步连续迭代改善,低于tol时终止训练。
-
validation_fraction : float, 可选, 默认 0.1,用作早期停止验证的预留训练数据集的比例,早0-1之间,只当early_stopping=True有用
-
beta_1 : float, 可选, 默认0.9,只有solver=’adam’时使用,估计一阶矩向量的指数衰减速率,[0,1)之间
-
beta_2 : float, 可选, 默认0.999,只有solver=’adam’时使用估计二阶矩向量的指数衰减速率[0,1)之间
-
epsilon : float, 可选, 默认1e-8,只有solver=’adam’时使用数值稳定值。
属性说明:
-
classes_:每个输出的类标签
-
loss_:损失函数计算出来的当前损失值
-
coefs_:列表中的第i个元素表示i层的权重矩阵
-
intercepts_:列表中第i个元素代表i+1层的偏差向量
-
n_iter_ :迭代次数
-
n_layers_:层数
-
n_outputs_:输出的个数
-
out_activation_:输出激活函数的名称。
方法说明:
-
fit(X,y):拟合
-
get_params([deep]):获取参数
-
predict(X):使用MLP进行预测
-
predic_log_proba(X):返回对数概率估计
-
predic_proba(X):概率估计
-
score(X,y[,sample_weight]):返回给定测试数据和标签上的平均准确度
-
set_params(**params):设置参数。