吴恩达机器学习课后作业——SVM支持向量机

支持向量机

一、作业内容

在本练习的前半部分，您将对各种示例2D数据集使用支持向量机(svm)。使用这些数据集进行试验将帮助您直观地了解支持向量机的工作方式，以及如何在支持向量机中使用高斯核。在练习的下一部分中，您将使用支持向量机构建一个垃圾邮件分类器。

数据集下载位置(包含吴恩达机器学课后作业全部数据集)：data

二、作业分析

1、支持向量机(SVM)(鲁棒性，大间距分类器)

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的 间隔最大的线性分类器 ，间隔最大使它有别于感知机；SVM还包括 核技巧 ，这使它成为实质上的非线性分类器。 SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。 SVM的的学习算法就是求解凸二次规划的最优化算法。

2、假设函数：
${\theta }^T$X $\ge$ 1，$h_{\theta }$(x) = 1
${\theta }^T$X $\le$ -1，$h_{\theta }$(x) = 0

3、定义y=1时，代价函数为$cos{t}_1$(z)。定义y=0时，代价函数为$cos{t}_0$(z)


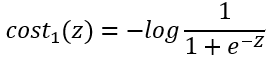
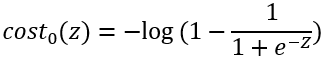
4、支持向量机的代价函数：

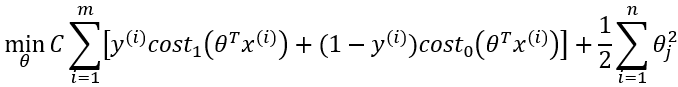
C:误差项惩罚系数
越大，容错率越低,越易过拟合,低偏差,高方差

5、SVM又称为大间隔分类器

向量的基本知识：
(1) $u^T$v=p*||u|| (向量的内积=v在u上投影的长度*u向量的模长)
(2) $u^T$v=$u_1$$v_1$+$u_2$$v_2$ （线代公式）
(3) p（v在u上投影的长度）是有方向的，如果大于90度则为负值。

假设${\theta }_0$=0，且特征数n=2，对于上一节最后的代价函数进行变形，我们可以得到以下等式：

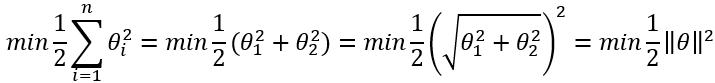
于是我们可以得到SVM决策边界：


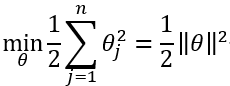
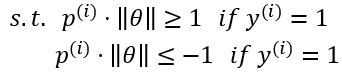
6、核函数：
将低维空间映射到高维空间
可以在低维空间计算出高维空间的点积结果

当出现非线性决策边界时，我们不知道几阶的多项式适合我们，我们可以使用核函数来构造新的特征。

(1) 首先我们定义了一些标记$l^1$、$l^2$、$l^3$。
(2) 接着我们构建了新的特征$f_1$、$f_2$、$f_3$。

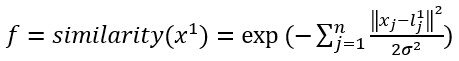
当x和l近似相等时，f等于1。当x和l距离比较远的话，f等于0

基于此，我们假设我们已经求出了最优的参数θ，下面就解释一下如何来进行分类：

(1) 首先是定义了三个标签$l^1$、$l^2$、$l^3$。接着我们放入样本x。
(2) 可以观察到x和$l^1$比较近，所以相似度比较高，则$f_1$≈1。而x和$l^2$、$l^3$比较远，所以相似度较低则$f_2$≈0、$f_3$≈0。
(3) 接着，我们代入表达式就可以计算出等于0.5，是大于0的，所以会分类为1。
(4) 同理我们可以将其他样本进行分类。

7、在实际应用中，我们如何选取标签$l^1$、$l^2$、$l^3$
(1) 将我们拥有的每一个样本点作为新的标记点
(2) 给新特征x,计算x与标记点的距离之和
(3) 构建完成后，使用支持向量机来进行预测
得到${\theta }^{T}f$ ≥ 0，判断y = 1。

8、C和标准差σ的选择

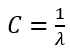
(1) 当C很大的时候，就相当于λ很小，也就相当于没有正则化，所以可能会出现过拟合（低偏差，高方差）。同理可得到相反情况。

(2) 当σ比较大的时候，高斯分布比较缓和，所得到的的曲线也比较缓和，所以会出现欠拟合现象（高偏差，低方差）。当σ比较小的时候，曲线没有那么缓和，就可能出现过拟合现象（低偏差、高方差）。

${\sigma }^2$：
(1)${\sigma }^2$大，特征变化较缓，高偏差，低方差。
(2)${\sigma }^2$小，特征变化较快，低偏差，高方差

9、逻辑回归与SVM比较：
逻辑回归对异常值敏感，SVM对异常值不敏感(抗噪能力强)——支持向量机改变非支持向量样本并不会引起决策面的变化；但是逻辑回归中改变任何样本都会引起决策面的变化。

对于大部分情况神经网络表现都很好，但是训练慢。且SVM是凸优化问题，因此总会找到一个全局最小值，不用担心局部极小的情况。

选择
当特征数量多、训练集数量较少时，一般选用逻辑回归或者不带核函数的SVM（线性核函数）
当特征数量少、训练集数量适中时，一般选用带高斯核函数的SVM
当特征数量少、训练集数量很大时，一般选用逻辑回归或者不带核函数的SVM（如果用高斯核函数可能过慢）

10、在python中使用高斯核函数：

(1) Scikit-learn(sklearn)是机器学习中常用的第三方模块，对常用的机器学习方法进行了封装，包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类(Clustering)等方法。里面包含了SVM的程序，直接调用调节参数即可。

(2) svm.SVC( ) 可以选择C值，以及核函数，调用之后先fit，再predict，predict时输入为一个二维数组，因此在画等高线的时候需要先把网格展开成二维数组进行predict再重新组成网格画图。在选择核函数时可以自己定义，例如：svm.SVC(kernel=my_kernel)，内置核函数默认为rbf高斯核,其中包含一个gamma关键词，gamma默认为1/n_features。

(3) gamma越小，模型复杂度越低，gamma越大，模型复杂度越高。

三、代码实战

在本练习中，我们将使用支持向量机（SVM）来构建垃圾邮件分类器。 我们将从一些简单的2D数据集开始使用SVM来查看它们的工作原理。 然后，我们将对一组原始电子邮件进行一些预处理工作，并使用SVM在处理的电子邮件上构建分类器，以确定它们是否为垃圾邮件。

引入所需函数库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
from sklearn import svm

首先我们要看一下这个简单的二维数据集，看看线性SVM如何对数据集进行不同的C值（类似于线性/逻辑回归中的正则化项）

我们将其用散点图表示，其中类标签由符号表示（+表示正类，o表示负类）。

# 加载数据
raw_data = loadmat('data/ex6data1.mat')

data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = raw_data['y']

positive = data[data['y'].isin([1])]
negative = data[data['y'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')
ax.legend()
plt.show()

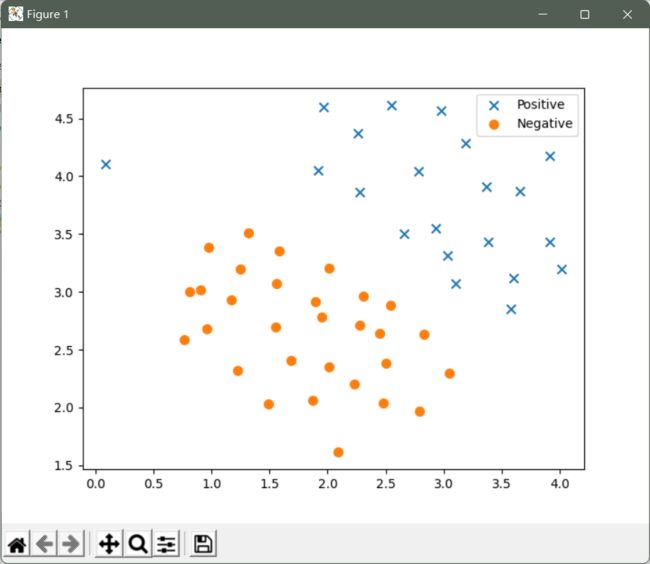
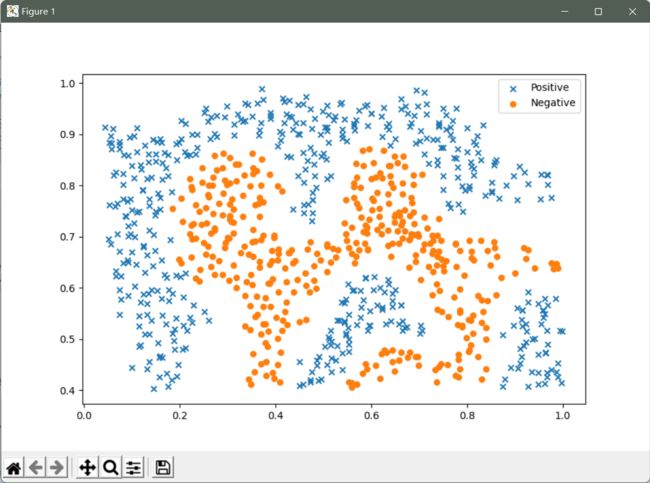
我们注意到，还有一个异常的正例在其他样本之外。 这些类仍然是线性分离的，但它非常紧凑。 我们要训练线性支持向量机来学习类边界。

在这个练习中，我们没有从头开始执行SVM的任务，所以我要用scikit-learn。

我们先设定误差项惩罚系数C=1

svc = svm.LinearSVC(C=1, loss='hinge', max_iter=1000)
svc.fit(data[['X1', 'X2']], data['y'])
svc.score(data[['X1', 'X2']], data['y'])

结果:

0.9803921568627451

然后，让我们将C的值增大到100

svc2 = svm.LinearSVC(C=100, loss='hinge', max_iter=1000)
svc2.fit(data_1[['X1', 'X2']], data_1['y'])
print(svc2.score(data_1[['X1', 'X2']], data_1['y']))

结果：

0.9411764705882353

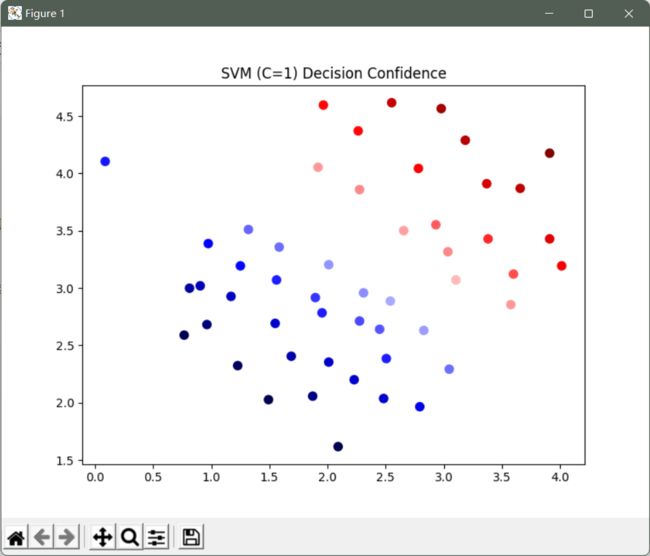
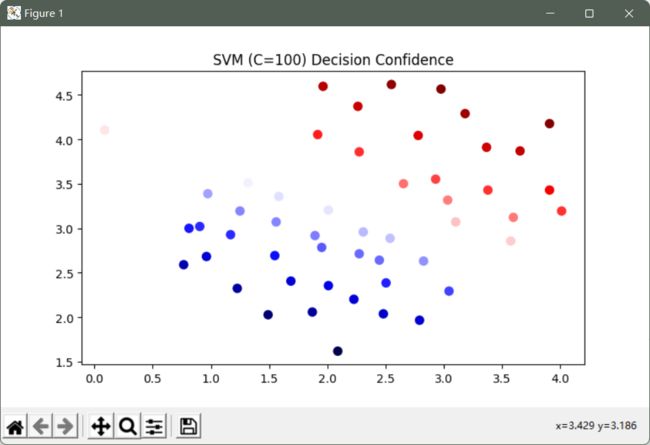
这次我们得到了训练数据的完美分类，但是通过增加C的值，我们创建了一个不再适合数据的决策边界。

我们可以通过查看每个类别预测的置信水平来看出这一点，这是该点与超平面距离的函数。

C=1的置信水平

data_1['SVM 1 Confidence'] = svc.decision_function(data_1[['X1', 'X2']])
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data_1['X1'], data_1['X2'], s=50, c=data_1['SVM 1 Confidence'], cmap='seismic')
ax.set_title('SVM (C=1) Decision Confidence')
plt.show()

C=100的置信水平

data_1['SVM 2 Confidence'] = svc2.decision_function(data_1[['X1', 'X2']])
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data_1['X1'], data_1['X2'], s=50, c=data_1['SVM 2 Confidence'], cmap='seismic')
ax.set_title('SVM (C=100) Decision Confidence')
plt.show()

现在我们将从线性SVM转移到能够使用内核进行非线性分类的SVM。 我们首先负责实现一个高斯核函数。 虽然scikit-learn具有内置的高斯内核，但为了实现更清楚，我们将从头开始实现。

# 高斯核函数
def gaussian_kernel(x1, x2, sigma):
    return np.exp(-(np.sum((x1 - x2) ** 2) / (2 * (sigma ** 2))))

实现一个高斯函数验证训练结果是否与预期值相符

x1 = np.array([1.0, 2.0, 1.0])
x2 = np.array([0.0, 4.0, -1.0])
sigma = 2

gaussian_kernel(x1, x2, sigma)

0.32465246735834974

该结果与练习中的预期值相符。

接下来，我们将检查另一个数据集，这次用非线性决策边界。

raw_data_2 = loadmat('ex6data2.mat')

data_2 = pd.DataFrame(raw_data_2['X'], columns=['X1', 'X2'])
data_2['y'] = raw_data_2['y']

positive = data_2[data_2['y'].isin([1])]
negative = data_2[data_2['y'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['X1'], positive['X2'], s=30, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=30, marker='o', label='Negative')
ax.legend()
plt.show()

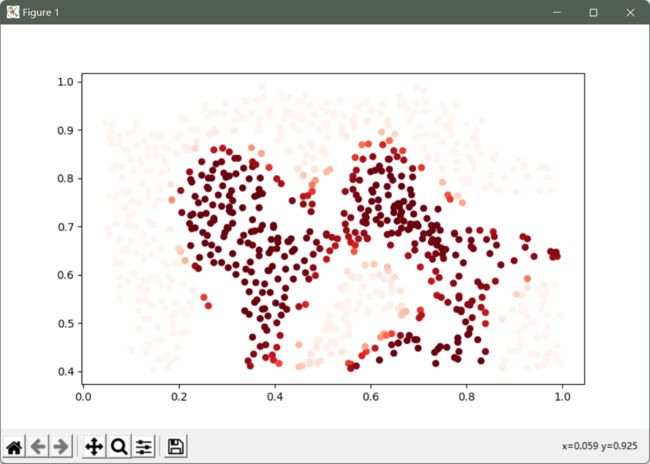
对于该数据集，我们将使用内置的RBF内核构建支持向量机分类器，并检查其对训练数据的准确性。

为了可视化决策边界，这一次我们将根据实例具有负类标签的预测概率来对点做阴影。

svc = svm.SVC(C=100, gamma=10, probability=True)
svc.fit(data_2[['X1', 'X2']], data_2['y'])
data_2['Probability'] = svc.predict_proba(data_2[['X1', 'X2']])[:,0]

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(data_2['X1'], data_2['X2'], s=30, c=data_2['Probability'], cmap='Reds')
plt.show()

从结果可以看出，它们大部分是正确的。

对于第三个数据集，我们给出了训练和验证集，并且基于验证集性能为SVM模型找到最优超参数。

# 加载数据
raw_data_3 = loadmat('ex6data3.mat')
X = raw_data_3['X']
Xval = raw_data_3['Xval']
y = raw_data_3['y'].ravel()
yval = raw_data_3['yval'].ravel()

# 基于验证集性能为SVM模型找到最优超参数
C_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
gamma_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]

best_score = 0
best_params = {'C': None, 'gamma': None}
for C in C_values:
    for gamma in gamma_values:
        svc = svm.SVC(C=C, gamma=gamma)
        svc.fit(X, y)
        score = svc.score(Xval, yval)

        if score > best_score:
            best_score = score
            best_params['C'] = C
            best_params['gamma'] = gamma

print(best_score, best_params)

得出最优超参数

0.965 {'C': 0.3, 'gamma': 100}

现在，我们将进行第二部分的练习。 在这一部分中，我们的目标是使用SVM来构建垃圾邮件过滤器。

# 加载数据集
spam_train = loadmat('spamTrain.mat')
spam_test = loadmat('spamTest.mat')

每个文档已经转换为一个向量，其中1899个维对应于词汇表中的1,899个单词。 它们的值为二进制，表示文档中是否存在单词。

# 每个文档已经转换为一个向量
# 它们的值为二进制，表示文档中是否存在单词
X = spam_train['X']
Xtest = spam_test['Xtest']
y = spam_train['y'].ravel()
ytest = spam_test['ytest'].ravel()

训练评估是用一个分类器拟合测试数据的问题。

使用SVM来构建垃圾邮件过滤器

svc = svm.SVC()
svc.fit(X, y)

计算训练集和测试集的精确度。

# np.round()浮点数取整
# 一般该函数遵循四舍五入原则，但是需要特别注意的是，当整数部分以0结束时，round函数一律是向下取整
# 例：np.round(10.5) >>> 10.0
print('Training accuracy = {0}%'.format(np.round(svc.score(X, y) * 100, 2)))
print('Test accuracy = {0}%'.format(np.round(svc.score(Xtest, ytest) * 100, 2)))

结果;

Training accuracy = 99.32%
Test accuracy = 98.7%

参考链接：https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
https://blog.csdn.net/weixin_41799019/article/details/118355127?spm=1001.2014.3001.5502