无监督特征对齐的迁移学习理论框架
0、前言
文献《基于无监督特征对齐的变负载下滚动轴承故障诊断方法》引入迁移学习中能够实现无监督领域适应的子空间对齐(subspace alignment,SA)算法并进行改进,提出将核映射方法与 SA 算法相结合。将训练数据和测试数据映射到相同高维空间,在高维空间的子空间进行特征对齐,以增加数据类间区分性,实现不同负载下源领域特征向目标领域特征对齐。具体理论可参考该文献。
1、无监督特征对齐
首先,究竟应该如何理解“对齐”?先看下述分析。
无监督特征对齐,顾名思义即不需要应用样本的标签信息。文章所述子空间对齐方法步骤如下:第一步,对不同领域的特征样本数据分别采用PCA方法确定投影矩阵,并将其作为源领域和目标领域子空间的基;第二步,采用线性变换的形式使得源领域子空间的基向目标领域子空间的基靠近,即实现源领域子空间和目标领域子空间的对齐,可以看出文章阐述的“对齐”更多的含义是对源域数据的投影矩阵H进行变换,使得变换后的结果尽可能接近目标域的投影矩阵(这样真的准确吗?)。还有为什么是“接近”而不直接“重合”呢?(重合意味着将源域的投影矩阵H强行等于目标域的投影矩阵B)为什么不这样呢?而且H变换后所得的矩阵A虽然接近目标域投影矩阵B,但是此时的A已经不能反应源域数据的分布特性了!谈不上A接近B就等价于两领域数据分布特性一致。所以文章不应该是直接对H进行变换,而应该是对源域数据本身进行变换,使得变换后数据空间的基接近或等于目标域数据空间的基。
此外,文中无监督特征对齐第一步采用PCA方法确定子空间的基,PCA确定的投影方向可以最大化投影后特征的分布方差,即子空间的基能反应原始数据的全局分布特性(这句话没毛病)。对齐两领域子空间的基使得两领域数据经过投影后的分布特征尽可能相似(真的是这样吗?投影矩阵接近即映射方向接近,但并不代表两领域数据经过投影后就接近啊!)。我们要的是最后的两领域数据分布接近,这是后续将不同领域数据进行联合分类训练或者回归训练建模的基础。
而且文章采用PCA方法是刻画不同领域数据的全局分布特性,有一定局限性。是否可以同时考虑局部和全局分布特性呢?当然这样做的难点是求取的投影矩阵很难满足正交条件(PCA求取的投影矩阵满足正交条件)。
综上所述 ,本人看该篇文一片雾水,理论没有说服我,所谓的“子空间基的对齐”并不是真正的两领域数据子空间对齐。而且真正的子空间对齐(subspace alignment,SA)算法目标函数也是对源域数据进行变换,以变换后的源域数据与目标域数据的Frobenius 范数值最小为目标求取变换矩阵。源域数据与目标域数据的Frobenius 范数值小意味着两领域数据全局分布很接近,可以简单粗暴理解为距离接近,是"一家人"。
2、无监督特征对齐的迁移学习理论框架
本人根据自己对SA算法的理解,并且考虑非线性特征降维以及联合分布特性等因素,提出一种无监督特征对齐迁移学习理论框架。
2.1 数据准备
① 源域:![]()
② 目标域:![]()
③求取目标域投影矩阵(基):![]() (反应目标域数据分布特性)
(反应目标域数据分布特性)
④定义源域转换矩阵:![]()
⑤假设转换后源域数据对应的投影矩阵(基)等于![]() (基对齐)
(基对齐)
⑥ 如果③中投影矩阵的求取是以最大化全局信息保留为原则,那么 源域转换矩阵求解的目标函数为:
![]()
约束条件: ![]() ,定义
,定义![]() 为
为![]() 最大m个特征值对应的特征向量矩阵。(m为降维后的特征维数)
最大m个特征值对应的特征向量矩阵。(m为降维后的特征维数)
⑦求解上述目标函数,可得源域转换矩阵![]() ,转换后的源域数据变成:
,转换后的源域数据变成:
![]()
此时的![]() 与目标域
与目标域![]() 数据结构一致(基对齐),为后续的特征提取和分类建模都做好了数据准备。接下来对
数据结构一致(基对齐),为后续的特征提取和分类建模都做好了数据准备。接下来对![]() 和
和![]() 进行联合特征提取和分类模型训练,可以弥补
进行联合特征提取和分类模型训练,可以弥补![]() 单独建模时数据量不够充分导致的模型泛化性能不够的问题。
单独建模时数据量不够充分导致的模型泛化性能不够的问题。
注意:上述是数据准备阶段的大致流程,步骤③中投影矩阵的求取方式实际上不唯一。以最大化全局方差信息保留为原则(即PCA方法)是线性化、非监督的典型方式,所得投影矩阵也满足正交条件。
2.2 特征提取
特征提取考虑三种形式:筛选、嵌入、抽象转换(神经网络提取的抽象特征)
筛选:就是特征筛选,从原有的特征中选一些重要的特征出来构成代表特征集。至于怎么判断重要就看各位如何选择了,基于不同的出发点选择出来的代表特征集也不尽相同(正所谓萝卜青菜各有所爱嘛)。
嵌入:对原有特征进行转换(线性或者非线性)得到新的特征表达,常见的就是PCA、KPCA基于全局方差信息;LPP、NPE、LE等流行学习方式;线性判别分析、fisher判别分析等监督降维方法;以及各种典型方法上的非线性化改进、参数改进、监督改进等等等等。。。
抽象转换:利用神经网络进行变换,特征输入神经网络,经过各层网络的抽象转换,形成抽象表达。(最火的就是深度学习嘛!)
特征提取方法太多,这里就不一一列举了,上述只是个人对特征提取进行了大致的归类(认知有限,仅供参考!!)
2.3 分类建模
特征提取完毕就可以进行分类建模了
分类方法也太多了,只要能将特征与标签对应起来的方法都可以是特定问题的分类方法。关键就看怎么将特征与标签对应起来了。针对特定分类问题,没有所谓最好的,只有更适合的分类模型。
3、结果验证
上述的框架包含三个层面,但是很明显后面两个层面是建立在第一个层面(数据准备)的基础上,第一个层面(特征对齐)才和标题更加密切相关,本文不对二、三层面做太多延申,只验证第一层面工作的意义。
验证方式:验证源域数据进行转换后与目标域联合建模相较于目标域数据单独训练建模的优势。
验证结果:
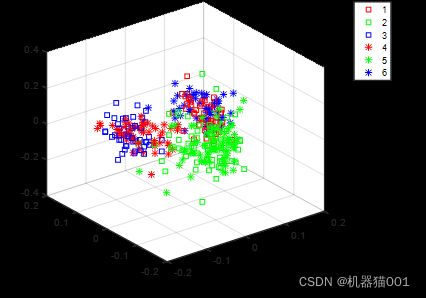
这是转换之前源域数据与目标域数据可视化情况(同颜色代表同类别,同现状代表同数据源):可以看出源域目标域数据分布差异大,不同类别相互重叠,对分类很不利。
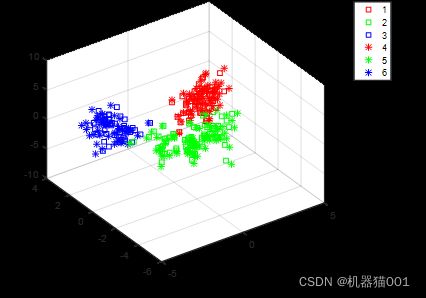
这是转换后的数据可视化情况(同颜色代表同类别,同现状代表同数据源):可以看出源域数据转换后与目标域数据重合度很高,因此转换后的源域数据可以和目标域数据一起进行建模,提高目标域的分类精度。
分类效果:采用相同分类器(SVM)进行分类建模
上图所示:所提迁移学习方法的分类准确率达到68%,直接将未转换的源域数据域目标域数据一起建模得到的分类准确率为26%,只利用目标域数据分类效果为41%。acc3甚至低于acc2是因为源域数据和目标域数据分布差异太大引起的(图1所示),反而干扰模型建立。acc1高出acc2超过20%,可见所提迁移学习框架是有效的。