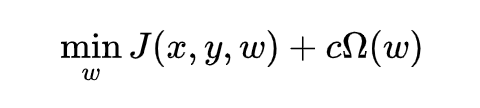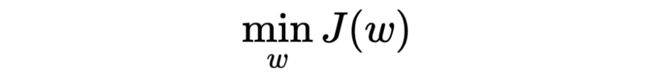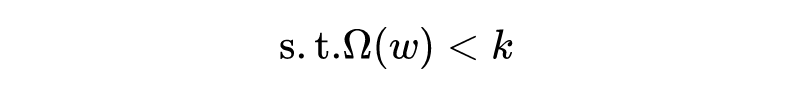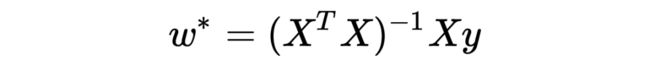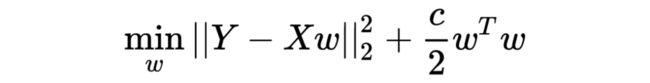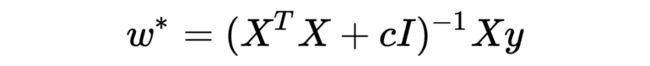全面讨论泛化 (generalization) 和正则化 (regularization)

来源：PaperWeekly
本文约8400字，建议阅读15分钟
本文和大家全面讨论机器学习和深度学习中的泛化和正则化。

模型泛化能力，是设计和评估一个机器学习 or 深度学习方法时无比重要的维度，所以我想通过一系列文章，与大家全面地讨论机器学习和深度学习中的泛化（generalization）/正则化（regularization），一方面从多角度理解模型的泛化问题，另一方面，从泛化角度来解释机器学习和深度学习中的很多方法（norm panalty, weight decay, dropout, parameter sharing等许多）。

这里的大部分内容基于 Ian Goodfellow 的《Deep Learning》一书第七章“Regularization for Deep Learning”（墙裂推荐！），并结合一些其他文章和我自己的经验。

这个系列的主要内容有：

引子

1. 定义：正则化（regularization）是所有用来降低算法泛化误差（generalization error）的方法的总称。

2. 正则化的手段多种多样，是以提升 bias 为代价降低 variance。

3. 现实中效果最好的深度学习模型，往往是【复杂的模型（大且深）】+【有效的正则化】。

目录：正则化方法（Regularizer）

1. Norm penalty：常用 L1/L2 regularization，理论机制不同，按特征方向重要性，L1 以阈值“削砍”参数分量，L2 “缩水”参数分量；深度学习中的实现方式有【weight decay】和【硬约束（重投影）】两种，各有不足。

2. L2-regularization 的特殊作用：解决【欠定问题】，调整协方差矩阵（covariance matrix）使其可逆。

3. Dropout layer 与 batchnorm layer：dropout 本质是一种 ensemble method；dropout 与 batchnorm 用于 regression 时有弊端；同时使用时理论上有冲突。

4. 深度学习的 Early stopping：减少 overfit 之后无意义的训练。 

1.引子（可以速读或略过哦）

定义：正则化（regularization）是所有用来降低算法泛化误差（generalization error）的方法的总称。

在机器学习中，为了让模型不局限于训练集上，我们通常采用很多手段来降低测试集误差（test error），或者说泛化误差（generalization error），未见过的新样本，我们也希望模型能表现良好。这些手段和方法又往往是以训练误差（training error）升高为代价的。所有用来降低泛化误差的手段和方法统称为正则化（regularization）；单独一种手段，可以称之为一个 regularizer。

手段多样，是以提升 bias 为代价降低 variance。

正则化的手段和方法多种多样，常见的比如给模型添加约束、给目标函数加惩罚项（其实是一种软约束）、模型集成（ensemble method）等等。采用约束或惩罚的手段，所起的作用可以是：融入先验（prior knowledge）、使模型变简单、把欠定问题转化成正定/超定问题（比如样本数量低于特征维度时，linear regression 无法使用，需要 ridge regression 才能有解）等等。

在深度学习中，对模型添加正则化，是以提升偏差（bias）为代价降低方差（variance）。一个有效的 regularizer，就是要很好地折中平衡 bias 和 variance，使 variance 大幅降低，而又不过度增加 bias。

现实中，效果最好的深度学习模型往往是【复杂的模型（大且深）】+【有效的正则化】。

现实的深度学习任务，比如处理图像、音频、文本，往往本身就是复杂的，因此我们设计复杂的神经网络结构，提供足够的模型容量（model capacity），才有可能描述输入-输出之间的复杂映射。神经网络中的参数取不同的值对应不同的模型，这些所有可能的模型构成了一个模型集（model class），大多数情况下，即使我们用复杂的结构，真实的映射也不在我们所选择的这个 model class 中。

然而，我们却又只有有限的数据，用有限的数据训练一个模型，即使真实的映射在 model class 中，我们一定能找到吗？不一定！因为训练使用的损失函数（loss）是经验损失（emperical loss，在训练样本上计算损失），并非真实损失（所有可能样本的损失），最终找到的模型只是在训练集上损失小。因此，我们不能放任样本过于复杂、只拟合训练数据，所以需要正则化。

下面就来逐一讨论不同的 regularizer 吧！

2.Norm Penalty，及其深度学习中的实现方式

假设模型输入为 ，输出为 ，参数为 ，在训练模型的过程中，解决优化问题  来求解参数 。Norm penalty 就是在原本的目标函数上，添加一个基于参数 norm 的惩罚项 ，新优化问题变成了：

 是个超参数，用来调整惩罚的力度， 相当于没有 regularization， 增加代表强化 regularization，实际使用过程中往往通过交叉验证来调整。 理论上是基于 L-p norm（任意 p）的函数，但常用的是 L1 和 L2-norm。

L1-regularization：基于 L1-norm 的惩罚项（向量 L1-norm 定义：），添加在回归模型也叫LASSO，优化问题变成了 ，能起到增强  稀疏性（sparsity）的特殊效果，在需要稀疏特征提取（feature selection）的情况下非常重要。

比如物体识别，如果一只猫的图片，头有点像狐狸，身子有点像狗，我们希望输出 ，而不是 猫狐狸狗 。另外，稀疏性表示（sparse representation）本身是一类 regularization，除了基于 L1 penalty 的方法，还有很多方式，我们之后会讨论到。

L2-regularization：模型的优化问题变成了 ，它在几乎所有的 ML 模型都可以用，也真的太常用了。

L1-regularization 促进稀疏性，L2-regularization 能降低模型容量，减少 overfitting，这已经是耳熟能详的。但从理论上看，他们究竟起了什么作用、怎样起的作用呢？我们先谈 L2，再谈 L1。

2.1 从理论角度看L2-regularization的机制

模型： 

从求解过程来看： ML 模型往往通过梯度下降法（gradient decent）来迭代更新参数，在第 k 个 iteration，更新公式为：， 是 learning rate。易见，L2-norm penalty 是通过在每一次迭代时以固定比例缩小、衰减参数，来避免复杂的模型。 基于此的实现手段称为 weight decay 我们稍后提到它的具体问题。

从最终解的结果来看： 添加 L2-regularization 后得到的解，相比于没有 regularization，究竟有什么区别？假设  为原优化问题的最优解，即 ，而  为加了 regularization 后的最优解，即 ，特征值分解提供了很好的视角。

首先我们对问题做一个简化，假设  为二次函数（quadratic function），如果它不是，那我们就在  周围对  做 quadratic 近似， 可以表达为 ，这里的 H 是 Hessian 矩阵。我们知道， 的最优解是一阶导 = 0 的解，也就有 ，也就有 。

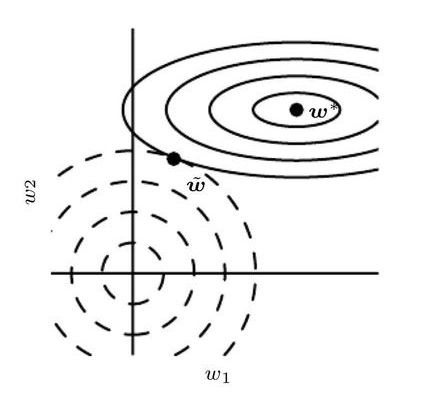
我们得到了  与  之间的变换关系，答案即将揭晓了！让我们做个特征值分解 ，得到 ，答案来了： 在 H 特征向量的方向上进行了缩放  ！ 具体地，在第  个方向上的参数分量，以  的倍率缩小，显然，特征值越小的方向，也就是不重要的方向上，缩小的程度越严重！

总结一下就是，L2-regularization 使重要方向上（目标函数非常敏感的方向）参数分量获得保存，在不重要的方向上得到衰减减，来实现精简参数的效果！

▲ L2-regularization 的工作机理：在不重要的方向上（图中横向：特征值小，目标函数不敏感）大幅衰减参数，在重要的方向上（图中纵向，特征值大，目标函数敏感）小幅衰减参数，最终实现降低模型复杂度的作用

2.2 从理论角度看L1-regularization的机制

模型： 

从求解过程来看： 由于 L1-norm 在  处不可导，我们无法使用梯度，而需要次梯度（subgradient）。在第 k 个 iteration，更新公式为：， 是 learning rate。易见，相比于没有 regularization，L1-regularization 在更新时额外根据参数的符号来调整，如果参数为正，就减少一点，如果为负，就增加一点，这样就使得参数向 0 靠近。因此，L1-regularization 是通过在每一次迭代时，依据符号调整数值，使其趋近于 0。

从最终解的结果来看： 我们以一个进一步简化的情况来讨论，假设 Hessian 矩阵  是对角线矩阵，（实际可能不是，但我们这里只想看一个最简单直观的例子），并假设对角线上的每个值 （保证目标函数是凸函数），我们和之前一样，对加入了 L1-regularization 的目标函数做一个二次函数近似 ，可以推导得出，L1-regularization 的最优解满足 。

答案揭晓了！L1-regularization 使低于一定阈值的参数全部清 0，高于阈值的参数减少一部分，来精简参数并迫使参数稀疏！具体地，在第  个维度上，如果 ，参数被直接逼成 0，这就造成了稀疏性；反之如果大于这个阈值，这个维度上的参数值被减少一定量，但溢出阈值的那部分被保留下来。

2.3 实现方式：weight decay与reprojection

具体地在 ML 和 DL 中，norm penalty 一般有两种方式实现，各有优劣。

第一种，最常用的，是 weight decay，根据 gradient descent 时的 update rule，我们只需要在每一次迭代对参数做一点衰减，尤其对于 L2-regularization，参数只需乘一个缩放引子。关于 weight decay 的使用和优劣有一些值得注意的地方。

1. 不作用于 bias：norm regularization 往往只用于限制 weights，我们基本不会对 bias 施加 regularization。因为 bias 本身不太会导致 variance 和 overfitting。当前的深度学习框架，weight decay 默认只作用于每一层 layer 的 weights。如果手动写 ML 模型，这一点要特别注意。

2. 给每层 NNlayer 不同的 decay？研究发现,在神经网络中，有时候每一层 layer 使用不同的 weight decay 常数会得到更好的效果。但是可能的组合太多了，很难找到最正确的配置。

第二种实现方式，是重投影，或者说硬约束法，这种方法求解的是一个与  等价的有约束优化问题：

它将参数的 norm 项作为一个“硬约束”来处理，而不是添加到目标函数中。具体如何实现呢？在每次 gradient descent 后，我们需要做一个重投影（reprojection），将参数投影到可行域  中最近的点。现有的研究提出了在神经网络中实施硬约束的策略：

• 对每一层神经网络的参数矩阵，约束其列向量的 norm，而不是整个矩阵的 norm。这样可以有效防止某一个神经元的 weight 过大。分析发现，这其实等价于对每个神经元的 weight，用不同的常数来做 weight decay。

然而，这两种实现方式各有优缺点，下面逐一分析：

1. weight decay 无差别地持续衰减参数会造成 dead unit：比较大型的任务中，我们训练很多个 epochs，即使我们常把 weight decay 常数设置的很小（比如 1e-4），经过很多次迭代更新，如果优化问题是非凸的，模型容易陷入一个参数值很小的局部最优点。

尤其在训练神经网络中，很可能造成死亡神经元（dead unit），也就是由于这里的参数太小，神经元的输出很小，对整体模型没什么存在的意义。而相比之下，硬约束的方式只有在   的时候才进行重投影， 时不操作，这样不会无差别地让参数趋向原点。

2. 重投影稳定性更高，可以使用较大的 learning rate。Hinton 的研究提出使用硬约束+大 learning rate 来快速探索参数，并保持稳定性。

3. 超参数的选择：当我们明确知道  中  的理想值，比如，我们明确想要  是一个 one-hot vector，也就是 ，那么重投影的方式可能更有用，如果采用 weight decay，我们很难准确找到对应某个  的那个合适的常数 ，因为它们之间没有明确的映射关系，我们不得不尝试不同的超参数来寻找最佳的值。

4. 选定常数后，weight decay 可以在更新参数的同时一步实现，但重投影则需要额外的步骤。

3.L2-regularization与【欠定问题】

上面提到的 L2-regularization，在特殊情况下，能使无法求解的欠定问题变得可解。这个角度并不是 regularization，但也是值得注意。

在 linear regression 模型中，我们知道，求解 linear regression  可以直接写出解析解（closed-form solution），需要对协方差矩阵 （covariance matrix）求逆：

然而，当样本数量 N 小于特征维度 D，这是个欠定的（underdetermined/under-constrained）问题，协方差矩阵不可逆，它的尺寸是 DxD，而秩是 。这意味着最大似然估计不存在。

此时的解决方案之一就是采用ridge regression，优化问题变成了

数学上与 L2-regularization 一模一样， 此时的解变成了

求逆的矩阵一个满秩的可逆矩阵，使欠定问题得以求解。从特征值的角度解释，协方差矩阵的特征值都是非负的，ridge regression 使所有特征值增加 c，保证所有特征值都为正，矩阵变得可逆。

4.Dropout layer

Dropout 与 batchnorm layer，是神经网络中无比常用的 layer，本文讨论一下他们促进泛化的机理、弊端、以及理论上存在的冲突。

4.1 促进泛化的机理是什么呢

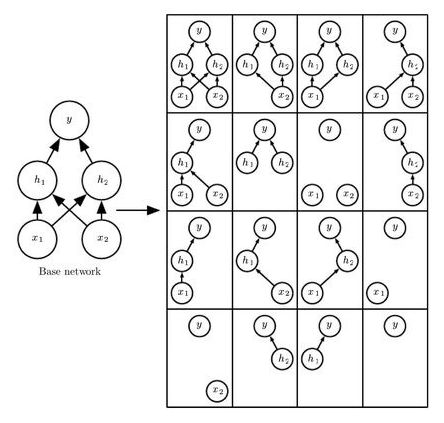
Dropout 是一种计算量低，但效果强大的 regularization。它的本质是一种集成模型（emsemble method），为什么这样说呢？在训练时，dropout layer 是通过随机生成一个蒙版（mask），按一定的概率，将部分神经元遮住，只使用剩余的神经元计算这一次的输出，下一个 iteration，生成一个新的随机 mask，遮住另一部分神经元。这样，各种可能的 mask 遮盖模型后，其实产生了各种各样的子模型，如图所示：

▲ Dropout layer：原模型用不同的遮盖方式，对应不同的子模型，训练的过程其实是在训练这些子模型的集合

训练神经网络的过程，其实是训练这些子模型的集合，也就是一堆子模型构成的 ensemble model。原理上，ensembling 本身对不同模型的输出取（加权）平均，解决了单个模型不稳定的问题，降低了 variance。我们之后会单独讲讲 ensemble method。

当然，这并不是 100% 地复刻 ensemble method，为什么呢？ 为了使有 dropout 和关掉 dropout（测试的时候 dropout 关闭）产生的输出结果具有相同的期望值，我们往往在训练时缩放参数或者神经元的值，比如，如果 dropout p=0.5，训练时可以将神经元们的输出 x2，来弥补缺少一部分神经元所带来的输出的损失，或者神经元的值不变，将参数 x2 来计算输出；也有一种方法是，训练不做改变，在测试（inference）的时候，让参数 x0.5。

但这种缩放不是完美的，当模型中有非线性的 hidden unit 时，输出结果的期望只是对 ensemble 输出期望值得一个近似，如果模型完全是现行的，输出的期望值被证明是完全等于 emsemble 的。

Dropout 的成功不是源于训练时的随机性，而是源于结合多个子模型时这种 bagging 效果，是一种“集体的智慧”。

另外，研究发现，dropout 应用于线性回归时，等价于一种 weight decay，但每个输入特征的 weight decay 常数不同，取决于这个特征的 variance。在其他线性模型上也有同样的结论。然而对深度模型，dropout不等价于 weight decay。

4.2 什么情况下dropout没有用，甚至使结果变差？

1. 模型不够大，足够复杂的模型才能抵消 dropout 带来的模型容量的降低；

2. 数据集很大很大，此时几乎所有的 regularization 方法都没什么作用了，且引入 dropout 运算增加的弊端远远盖过了 regularization 带来的好处；

3. 有标签的训练数据（labeled data）太少，研究发现此时贝叶斯神经网络（bayesian neural network）性能远超 dropout，半监督学习也胜过 dropout。

4.3 与batchnorm一起使用时的问题：variance shift

实际上，我们经常发现 dropout 和 batchnorm 一起使用，比如 DNN 中这样搭配

layers = [
            nn.Linear(in_size, 1024),
            nn.BatchNorm1d(1024),
            nn.ReLU(),
            nn.Dropout(0.2),
            ......

然而，有研究提出，dropout 和 batchnorm 一起用时有可能会使效果变差，这是因为，当我们结束训练进入测试时，dropout 会改变一个神经元的方差（variance），而 batchnorm 由于归一化，在测试时，则会致力于保持训练时所累积的统计方差。这种 variance 上的冲突，被称为 variance shift，研究发现他会导致测试阶段不稳定。有兴趣的可以详细阅读这篇文章“Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift”。

尽管理论上存在这样的冲突，在目前的很多开源模型中，不难发现两者搭配使用却如此的流行并且具有可观的性能，这一理论的冲突也被多数人所忽视。更确切的结论可能还需要进一步的研究和验证。

5.Early stopping

在训练复杂模型时，我们可能经常发现，在训练了很多epoch后，测试误差先减少后有逐渐增加，此时意味着模型产生了过拟合（overfitting），已经变得不好了。

为了获得测试误差最低，泛化能力最好的模型，我们可以采用 early stopping，在训练时注意阶段性地保存模型，当发现 overfitting 时，就可以停止训练节省时间，并返回测试结果最好的模型。

听起来好像是一些废话，但从泛化的角度上看，early stopping 实现了一个模型选择（model selection）的过程，而且努力减少了不必要的训练。

大致上，early stopping 需要一下几个元素：

• 预热时长 -n：先预训练 n 个 epochs，不测试模型，之后开始训练+测试+训练+测试.....

• 耐心 -p：当连续 p 个 epochs 都观测到测试结果变差，则放弃训练

• 最佳模型：训练过程中保存和更新迄今为止的最佳模型

具体的 early stopping 算法也有很多变体，比如预热时在小数据集上训练若干 epochs，之后在完整数据集上训练并测试若干 epochs，中途若测试误差高于预热时的训练误差，则放弃训练。

编辑：王菁
校对：林亦霖