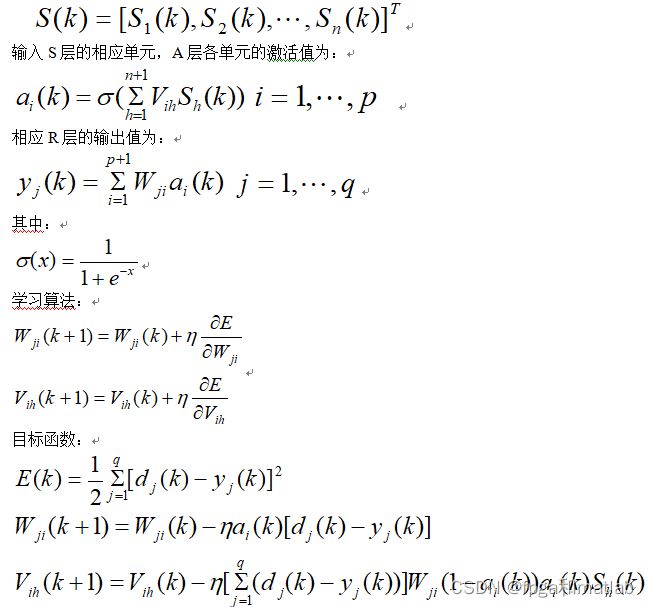基于神经网络的预测模型控制器matlab仿真
目录
一、理论基础
二、案例背景
1.问题描述
2.思路流程
三、部分MATLAB仿真
四、仿真结论分析
五、参考文献
一、理论基础
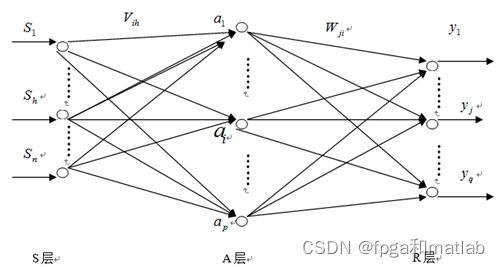
简单的介绍一下BP神经网络：
给定一组样本：
MPC方法一个潜在的弱点是优化问题必须能严格地按要求推算，尤其是在非线性系统中。模型预测控制已经广泛地应用于线性MPC问题中，但为了减小在线计算时的计算量，该部分的计算为离线。
一个非常强大的函数逼近器为神经网络，它能很好地用于表示非线性模型或控制器。基于模型跟踪控制的方法已经普遍地应用在神经网络控制，这种方法的一个局限性是它不适合于不稳定地逆系统，基此本文研究了基于优化控制技术的方法。
许多基于神经网络的方法已经提出了应用在优化控制问题方面，该优化控制的目标是最小化一个与控制相关的代价函数。一个方法是用一个神经网络来逼近与优化控制问题相关联的动态程式方程的解。
考虑一个离散非线性控制系统：
为在K+N时刻时的无穷小，得出当
时的无穷优化控制问题的解，同样就能得到有穷优化问题。对于非线性系统，优化控制问题一般无闭式解，因此，本文研究强力和不最理想的方法。在模型预测控制（MPC）中，控制信号的确定是通过在每个采样时刻输入序列为
时，最小化代价函数（2）。只有优化输入序列的第一个元素u（k）作为系统的输入，在下一个采样时刻k+1，新的优化问题是对于给定的优化控制问题而言的。在这种方法中，终止条件
可以看作是一个当时刻K+N趋于无穷时最小化代价函数的逼近器，但实际上更多的是用于保证闭环的稳定性。模型预测控制方法有一个非线性的缺点，且需要通过在每个采样时刻得到受约束的优化问题，同时需要通过在线计算来实现。
二、案例背景
1.问题描述
CV 是冷水阀的开度 in % CV
Oat 是外界温度 单位是摄氏度
ZT 是室内温度 单位是摄氏度
CV_V OAT_V和ZT_V 都是用来做模型校准的；
CV，OAT和ZT （30天）是用来做模型训练的。
目的是通过控制冷水阀的开度来调节室内温度，目前该系统采用的是一个简单的比列调节控制。
2.思路流程
1. 建一个神经网络预测模型
2. 通过这个模型计算出一个优化的冷水阀的控制路径，因为没法连接到实际系统上，只要是open loop的就可以。
三、部分MATLAB仿真
仿真程序如下所示：
clc;
clear;
close all;
warning off;
addpath 'func\'
%%
%初始化参数
%初始化参数
%仿真时间长度
ALL_Times = 200;
%神经网络学习率
Learn_Rate = 0.1;
Alpha = 0.05;
%网络维度
Nums = 10;
Nums2 = 4;
%初始化随机权值
w2 = rand(Nums,1);
w2d1 = w2;
w2d2 = w2;
%初始化随机权值
w1 = rand(Nums2,Nums);
w1d1 = w1;
w1d2 = w1;
dw1 = zeros(size(w1));
u_1 = 0;
y_1 = 0;
I = zeros(Nums,1);
Iout = zeros(Nums,1);
FI = zeros(Nums,1);
State = zeros(Nums2,1);
t = 0.001.*(1:ALL_Times);
%%
%参考轨迹
%参考轨迹
yr = zeros(ALL_Times,1);
yr = func_reference(ALL_Times);
number1 = 25;
number2 = 16;
Set_Vlaue = 10;
yout_1 = 0;
cube_define;
%%
%循环仿真
%循环仿真3
for k=2:2*ALL_Times-10
if k <= ALL_Times%在线辨识学习
%控制器
[yout,Errs,u] = func_controller0(y_1,K,e,Set_Vlaue,u,A0,k,ALL_Times,number1,number2);
%输出
ym = func_ym0(yr,u,k,ALL_Times);
%计算误差
e(k) = ym(k)-yout(k);
State(1) = yout(k);
State(2) = yout(k-1);
State(3) = u(k);
State(4) = u(k-1);
%在线神经网络训练
%Inner network
for j=1:1:Nums
I(j) = State'*w1(:,j);
Iout(j) = 1/(1+exp(-I(j)));
end
%Output of network
err_estimate(k) = w2'*Iout;
e1(k) = err_estimate(k)-e(k);
%Updata the weight
w2 = w2d1-(Learn_Rate*0.1*e1(k))*Iout+Alpha*(w2d1-w2d2);
for j=1:1:Nums
FI(j)=exp(-I(j))/(1+exp(-I(j)))^2;
end
for i=1:1:Nums2
for j=1:1:Nums
dw1(i,j)=e1(k)*Learn_Rate*FI(j)*w2(j)*State(i);
end
end
w1 = w1d1+dw1+Alpha*(w1d1-w1d2);
w1d2 = w1d1;
w1d1 = w1;
w2d2 = w2d1;
w2d1 = w2;
else
%开始实际的工作
Ind = k-ALL_Times+2;
%被控对象
yout(Ind) = func_system_model(y_1,u_1);
%控制器输出
[Uk_1,Y0,u_1,yout_1,e,SetPoint_Vlaue,Errs,Det,u] = func_controller(yout,A0,err_estimate,u,Ind,ALL_Times,Set_Vlaue,number1,K,number2);
%辨识输出
[State,err_estimate,e,temp]=func_Bpann(I,Iout,err_estimate,yr,u,Ind,ALL_Times,State,w1,w2,Nums);
if Ind-ALL_Times <= 0
ym(Ind) = temp;
else
ym(Ind) = temp+yr(ALL_Times)*u(Ind-ALL_Times);
end
if Ind+1-ALL_Times <= 0
ym1(Ind+1) = temp;
else
ym1(Ind+1) = temp+yr(ALL_Times)*u(Ind+1-ALL_Times);
end
%延迟
%延迟
State(1) = yout(Ind);
State(2) = yout(Ind-1);
State(3) = u(Ind);
State(4) = u(Ind-1);
end
end
Start = 1;
Ends = length(yout)-10;
y_real = yout(Start:Ends);
y_pred = ym(Start:Ends);
y_pred1 = ym1(Start:Ends);
U_cont = u(Start:Ends);
Times = t(Start:Ends);
figure;
subplot(211);
plot(Times,y_pred,'b','linewidth',2);
hold on
plot(Times,y_real,'r','linewidth',1);
hold off
grid on
legend('预测输出','模型输出');
xlabel('Time')
ylabel('振幅')
subplot(212);
plot(Times,U_cont,'k','linewidth',2);
legend('控制u')
xlabel('Time')
ylabel('振幅')
grid on
figure;
subplot(211);
plot(Times,y_pred1,'b','linewidth',2);
legend('预测输出')
xlabel('Time')
ylabel('振幅')
grid on
subplot(212);
plot(Times,abs(y_real-y_pred),'r','linewidth',2);
xlabel('Time')
ylabel('误差')
grid on
Err = abs(mean(y_real(round(length(y_real)/2):end)-y_pred(round(length(y_pred)/2):end)));
disp('误差：');
Err
四、仿真结论分析
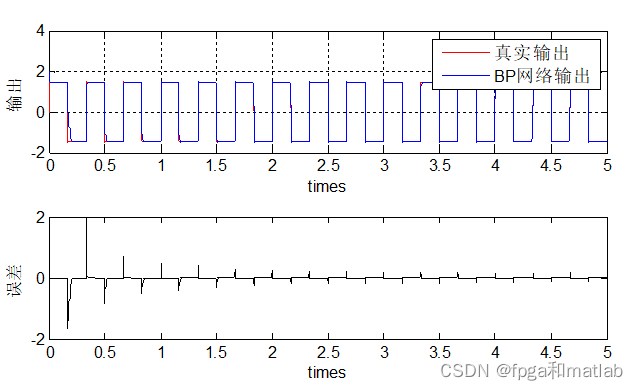
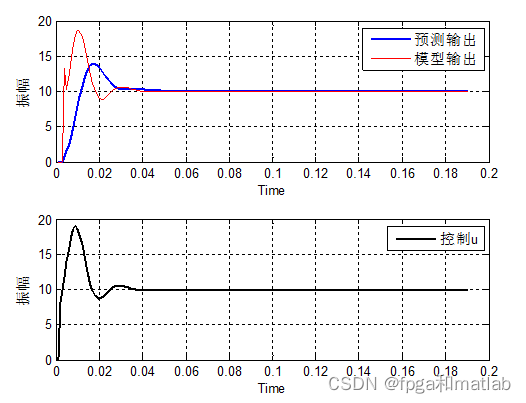
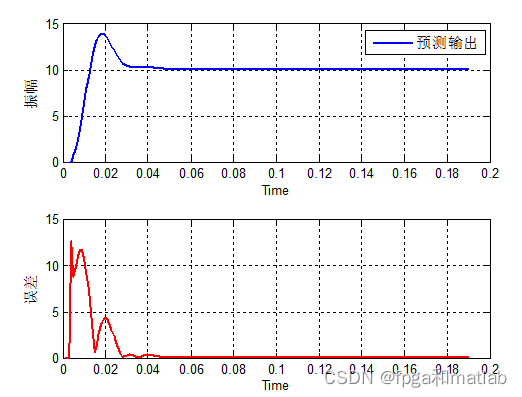
这里，我们将系统的模型简化为一个简单的控制对象，在实际中，我们只需要对其进行替换即可。具体的仿真如下所示：
预测模型就是一个基于神经网络的辨识系统。通过这个模型，可以获得系统的辨识结果，在通过该模型的在线学习之后获得辨识结果，然后再系统的后面时刻，即可通过该辨识结果进行模型预测控制输出。
五、参考文献
[1]高龙, 杨奕, 任晓琳,等. 基于BP神经网络的空气源热泵温度MPC策略[J]. 控制工程, 2021, 28(9):8.A08-22