吴恩达机器学习课后作业

01-linear regression

线性回归预备知识

假设函数与损失函数：

梯度下降函数

为了方便运算，我们需要将各个函数计算转为矩阵计算
（一）假设函数向量化

（二）损失函数向量化

（三）梯度下降函数向量化

综上

单变量线性回归（ 一个特征值）

入口 利润

#开发人员：肖本杰
#阶   段 ：学习
#开发时间：2022/8/1 17:02
#单变量线性回归 一个特征值

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
'''
numpy :科学计算库，处理多维数组，进行数据分析
pandas :是基于NumPy 的一种工具，该工具是为了
        解决数据分析任务而创建的
Matplotlib:Python 的 2D绘图库
matplotlib.pyplot：提供一个类似matlab的绘图框架
'''

#导入文件#
data = pd.read_csv('ex1data1.txt',sep=',',names=['population','profit']) #读取文件   names列表指定列名
# print(data.head())  #查看前五个数据
# print(data.tail())  #查看后五个数据
# print(data.describe()) #查看数据描述

#可视化#
'''
画散点图
data.plot.scatter('population','profit',c='b',label='population',s=30)
第一个参数为横轴名称，第二个参数为纵轴名称，第三个参数为颜色，第四个参数为标签，第五个参数为散点大小
'''
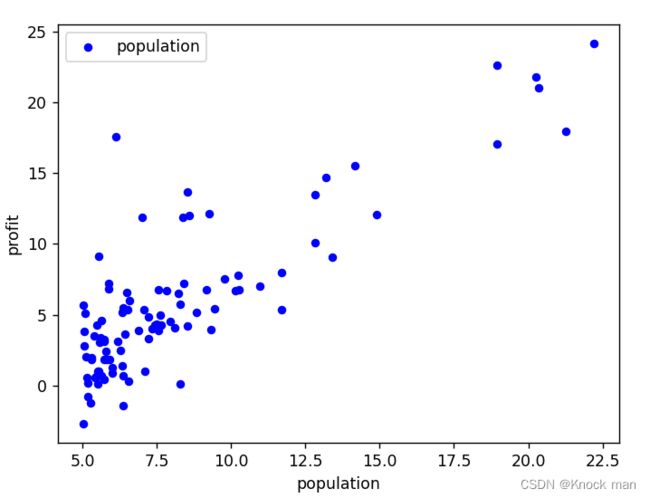
data.plot.scatter('population','profit',c='b',label='population',s=20)
plt.show()

#在第一列插入一列1
'''
DataFrame.insert(loc, column, value, allow_duplicates=False)
1. loc: 插入的列索引
2. column: 插入列的标签,字符串
3. value ：插入列的值
'''
data.insert(0,'ones',1) #插入
#print(data.head())
'''
   ones  population   profit
0     1      6.1101  17.5920
1     1      5.5277   9.1302
2     1      8.5186  13.6620
3     1      7.0032  11.8540
4     1      5.8598   6.8233
'''

#切片取出数据集形成矩阵
'''
data.iloc[起始行:终止行,起始列，终止列]
'''
X = data.iloc[:,0:2]  #所有行，0列和1列
#print(x.head())
y = data.iloc[:,2:]
#print(y.head())

#将数据转化为数组
X = X.values
y = y.values
y = y.reshape(97,1) #y转化为二维数组方便运算

#定义损失函数
def costFunction(X,y,theta):
    inner = np.power(X @ theta - y,2)
    return np.sum(inner)/(2 * len(X))

#初始化theta
theta = np.zeros((2,1))  #初始theta全为0
print(costFunction(X,y,theta))

#梯度下降函数
def gradienDescent(X,y,theta,alpha,iters):
    costs = []
    for i in range(iters):
        theta = theta - (X.T @ (X@theta - y)) * alpha / len(X)  #迭代梯度下降
        cost = costFunction(X,y,theta) #代价函数值保存
        costs.append(cost)
    return theta,costs

#初始化α，迭代次数
alpha = 0.02
iters = 2000

theta,costs = gradienDescent(X,y,theta,alpha,iters)

#可视化代价函数图像
fig,ax = plt.subplots()
ax.plot(np.arange(iters),costs) #画直线图
ax.set(xlabel = 'iters',ylabel='cost',title = 'cost vs iters')  #设置横纵轴意义
plt.show()

x = np.linspace(y.min(),y.max(),100) #代表横坐标取值
y_ = theta[0,0]+theta[1,0] * x #拟合直线函数


#拟合函数可视化
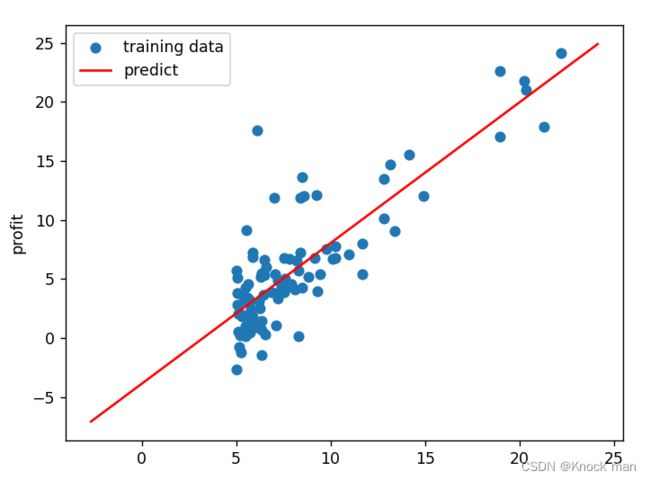
fig,ax = plt.subplots()
ax.scatter(X[:,1:2],y,label='training data') #画散点图

ax.plot(x,y_,'r',label='predict') #画假设函数直线图
ax.legend()
ax.set(label='population',ylabel='profit')
plt.show()

画特征值散点图

梯度下降过程（损失函数变化曲线）

最终假设函数的拟合效果

单变量线性回归（ 多个特征值）

房屋大小 房间数 价格

#开发人员：肖本杰
#阶   段 ：学习
#开发时间：2022/8/13 15:05
#单变量线性回归 多个特征值
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#读取文件
data = pd.read_csv('ex1data2.txt',sep=',',names=['size','bedrooms','price']) #读取文件   names列表指定列名

#特征归一化
def normalize_feature(data):
    return (data - data.mean()) / data.std() #（数据 - 平均值）/方差
data = normalize_feature(data)
print(data.head())

#特征值可视化
data.plot.scatter('size','price',c='b',label='bedrooms',s=20)  #画卧室数与价格的散点图
plt.show()
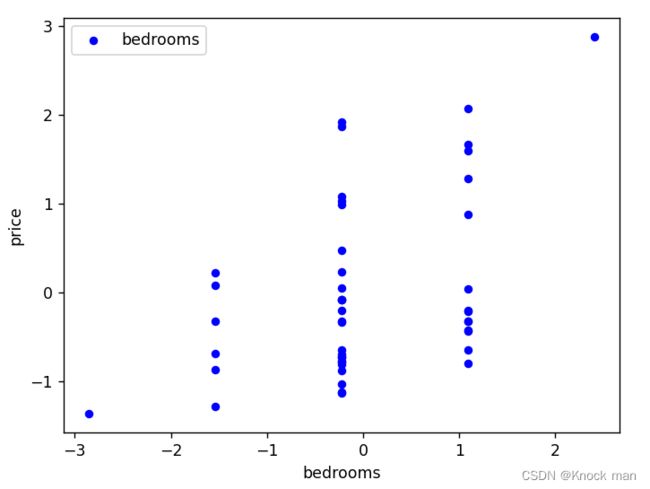
data.plot.scatter('bedrooms','price',c='b',label='bedrooms',s=20)   #画房间大小与价格的散点图
plt.show()

#插入一列1
data.insert(0,'ones',1) #插入
print(data.head())
#构造数据集
X = data.iloc[:,0:3]
y = data.iloc[:,3:4]

#将dadaframe转成数组
X = X.values #(47,3)
y = y.values #(47,)
y = y.reshape(47,1)

#损失函数
def costFunction(X,y,theta):
    inner = np.power(X@theta - y,2)
    return np.sum(inner)/(2*len(X))

theta = np.zeros((3,1))

#梯度下降函数
def gradienDescent(X,y,theta,alpha,iters):
    costs = []
    for i in range(iters):
        theta = theta - (X.T @ (X@theta - y)) * alpha / len(X)  #迭代梯度下降
        cost = costFunction(X,y,theta) #代价函数值保存
        costs.append(cost)
    return theta,costs

#不同的alpha的效果
candinate_alpha = [0.0003,0.003,0.03,0.001,0.01]
iters = 2000

#绘图
fig,ax = plt.subplots()
for alpha in candinate_alpha:
    _,costs = gradienDescent(X,y,theta,alpha,iters)
    ax.plot(np.arange(iters),costs,label = alpha)
    ax.legend()
ax.set(xlabel='iters',ylabel='cost',title='cost vs iters')
plt.show()

房间大小特征与价格的散点图

房间数量特征与价格的散点图

不同的学习率，损失函数的下降情况

单变量线性回归（ 正规方程）

人口 利润

#开发人员：肖本杰
#阶   段 ：学习
#开发时间：2022/8/13 15:05
#单变量线性回归 多个特征值

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv('ex1data1.txt',sep=',',names=['population','profit'])
data.insert(0,'ones',1) #插入#print(data.head())
X = data.iloc[:,0:2]  #所有行，0列和1列
y = data.iloc[:,2:]
X = X.values
y = y.values
y = y.reshape(97,1) #y转化为二维数组方便运算

#正规方程函数
def normalEquation(X,y):
    theta = np.linalg.inv(X.T @ X) @ X.T @ y
    return theta
theta = normalEquation(X,y)
print(theta)