吴恩达机器学习课后作业——多元分类

一、手写多分类

一、作业内容

自动手写数字识别在今天被广泛使用——从识别信封上的邮政编码(邮政编码)到识别银行支票上写的金额。在本练习中，您将使用逻辑回归和神经网络来识别手写数字(从0到9)。您将扩展之前的逻辑回归实现，并将其应用于one-vs-all分类。
数据集下载位置(包含吴恩达机器学课后作业全部数据集)：data

二、作业分析

1、数据以.mat格式储存，mat格式是matlab的数据存储格式，按照矩阵保存，与numpy数据格式兼容，适合于各种数学运算，因此主要使用numpy进行运算。

2、数据中有5000个训练样例，其中每个训练样例是一个20×20像素灰度图像的数字，每个像素由一个浮点数表示，该浮点数表示该位置的灰度强度。每个20×20像素的网格被展开成一个400维的向量。这些每个训练样例都变成数据矩阵X中的一行。这就得到了一个5000×400矩阵X，其中每一行都是手写数字图像的训练样例。训练集的第二部分是一个包含训练集标签的5000维向量y，“0”的数字标记为“10”，而“1”到“9”的数字按自然顺序标记为“1”到“9”。

3、多元分类：如果我们要分成的类数大于2，我们通常就称之为多分类问题。对于多元分类问题的原理，我们也称为“一对余”方法。

4、我们可以将多元分类问题转化为n个二元分类问题，对于n个独立的二元分类问题，可以分别拟合n个分类器，$h_{\theta }^1$(x)、$h_{\theta }^2$(x)、…$h_{\theta }^n$(x)，也就是产生了n个决策边界。

5、当我们进行预测的时候，我们给出一个新的输入值x，然后我们需要在这三个分类器中分别运行输入x，然后选择$h_{\theta }^i$(x)最大的类别，也就是选择可行度最高的、分类效果最好的，我们预测y就是那个值。

6、读入.mat文件
(1)Scipy：是一个高级的科学计算库，它和Numpy联系很密切
(2)Scipy一般都是操控Numpy数组来进行科学计算
(3)Scipy有很多子模块可以应对不同的应用，例如插值运算，优化算法，图像处理，数学统计等。
(4)scipy.io：数据输入输出
(5)loadmat

7、关于模型训练所用到的代价函数和梯度下降等知识点，见上一章，逻辑回归。

三、代码实战

引入所需函数库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from  scipy.io import loadmat
from scipy.optimize import minimize

首先我们加载数据，并将我们的逻辑回归实现修改为完全向量化（即没有“for”循环）。这是因为向量化代码除了简洁外，还能够利用线性代数优化，并且通常比迭代代码快得多。

# 加载数据
data = loadmat('ex3data1.mat')
# 图像在martix X中表示为400维向量(其中有5000个)
# print(data['X'].shape, data['y'].shape)
# (5000, 400) (5000, 1)

rows = data['X'].shape[0]
params = data['X'].shape[1]

all_theta = np.zeros((10, params + 1))

X = np.insert(data['X'], 0, values=np.ones(rows), axis=1)

theta = np.zeros(params + 1)

y_0 = np.array([1 if label == 0 else 0 for label in data['y']])
y_0 = np.reshape(y_0, (rows, 1))

首先我们编写sigmoid 函数，用以得到逻辑回归模型的假设函数

# sigmoid 函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

然后我们再编写代价函数来评估结果

# 代价函数
def cost(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:, 1:theta.shape[1]], 2))
    return np.sum(first - second) / len(X) + reg

如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对0 进行正则化，所以梯度下降算法将分两种情形：

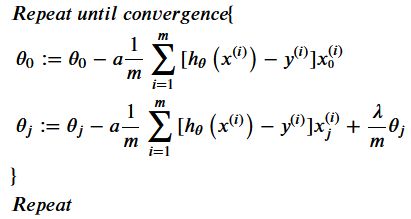
以下是原始代码是使用for循环的梯度函数：

# 梯度下降(使代价函数最小化)
def gradient_with_loop(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)

    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)

    error = sigmoid(X * theta.T) - y

    for i in range(parameters):
        term = np.multiply(error, X[:,i])

        if(i == 0):
            grad[i] = np.sum(term) / len(X)
        else:
            #theta正则化
            grad[i] = (np.sum(term) / len(X) + (learningRate / len(X)) * theta[:,i])
    return grad

向量化代码除了简洁外，还能够利用线性代数优化，并且通常比迭代代码快得多。
向量化的梯度函数

# 向量化梯度函数
def gradient(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)

    parameters = int(theta.ravel().shape[1])
    error = sigmoid(X * theta.T) - y

    grad = ((X.T * error) / len(X)).T + ((learningRate / len(X)) * theta)

    # 截距梯度没有正则化
    grad[0, 0] = np.sum(np.multiply(error, X[:,0])) / len(X)

    return np.array(grad).ravel()

现在我们可以开始构建分类器，对于这个任务，我们有10个可能的类，并且由于逻辑回归只能一次在2个类之间进行分类，我们需要多类分类的策略。
在本练习中，我们的任务是实现一对一全分类方法，其中具有k个不同类的标签就有k个分类器，每个分类器在“类别 i”和“不是 i”之间决定。 我们将把分类器训练包含在一个函数中，该函数计算10个分类器中的每个分类器的最终权重，并将权重返回为K*(特征数+1)数组，其中n是参数数量。

# 构建分类器
def ones_vs_all(X, y, num_labels, learning_rate):
    rows = X.shape[0]
    params = X.shape[1]

    # k X (n + 1)数组中每个分类器的参数
    all_theta = np.zeros((num_labels, params + 1))

    # 要加上偏置单元的列，也就是加上一列全1
    X = np.insert(X, 0, values=np.ones(rows), axis=1)

    # 标签是1-indexed而不是0-indexed
    # 遍历每一种分类器
    for i in range(1, num_labels + 1):
        # 初始化当前分类器的theta数组
        theta = np.zeros(params + 1)
        # 因为在进行二元分类时，真实值只可能为0和1
        # 多元分类中，采用的是一对多的思想
        # 因此下面这行就是除了当前分类，其他y值全部设置为0
        y_i = np.array([1 if label == i else 0 for label in y])
        y_i = np.reshape(y_i, (rows, 1))

        # 最小化目标函数
        fmin = minimize(fun=cost, x0=theta, args=(X, y_i, learning_rate), method='TNC', jac=gradient)
        
        # 将当前分类器的theta数组整合到总的theta数组中
        # 通过fmin.x可以获得对应的theta
        all_theta[i-1,:] = fmin.x

    return all_theta

最后我们使用训练完毕的分类器预测每个图像的标签。
我们将计算每个类的类概率，对于每个训练样本（使用向量化代码），并将输出类标签为具有最高概率的类。

# 使用训练完毕的分类器预测每个图像的标签
def predict_all(X, all_theta):
    rows = X.shape[0]
    params = X.shape[1]
    num_labels = all_theta.shape[0]

    # 和之前一样，插入一些以匹配形状
    # 插入偏置单元，也就是全为1的列
    X = np.insert(X, 0, values=np.ones(rows), axis=1)

    # 转化为矩阵
    X = np.matrix(X)
    all_theta = np.matrix(all_theta)

    # 计算每个类在每个训练实例上的类概率
    h = sigmoid(X * all_theta.T)

    # 以最大概率创建索引数组
    h_argmax = np.argmax(h, axis=1)

    # 因为我们的数组是0-indexed的，所以我们需要为真标签预测添加一个indexed
    h_argmax = h_argmax + 1

    return h_argmax

我们可以使用predict_all函数为每个实例生成类预测，看看我们的分类器是如何工作的。

# 使用predict_all函数为每个实例生成类预测
all_theta = ones_vs_all(data['X'], data['y'], 10, 1)
y_pred = predict_all(data['X'], all_theta)
correct = [1 if a == b else 0 for (a, b) in zip(y_pred, data['y'])]
accuracy = (sum(map(int, correct)) / float(len(correct)))
print('accuracy = {0}%'.format(accuracy * 100))

输出准确率

accuracy = 94.46%

参考链接：https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
https://blog.csdn.net/m0_51933492/article/details/123892518?spm=1001.2014.3001.5502