wespten

密码学与加密算法详解

一、密码学概述

密码学已经从第一代广泛应用的密码学算法（比如已经退役的 MD5 跟 DES），发展到现代密码学算法（如 SHA-3, Argon2 以及 ChaCha20）。

让我们首先跟一些基本的密码学概念混个脸熟：

哈希函数，如 SHA-256, SHA3, RIPEMD 等
散列消息认证码 HMAC
密钥派生函数 KDF，如 Scrypt
密钥交换算法，如 Diffie-Hellman 密钥交换协议
对称密钥加密方案，如 AES-256-CTR-HMAC-SHA-256
使用公私钥的非对称密钥加密方案，如 RSA 和 ECC, secp256k1 曲线跟 Ed25519 密码系统
数字签名算法，如 ECDSA
熵（entropy）与安全随机数生成
量子安全密码学

上述这些概念涉及到技术被广泛应用在 IT 领域，如果你有过一些开发经验，可能会很熟悉其中部分名词。如果不熟也没任何关系，本书的目的就是帮你搞清楚这些概念。

这个系列的文章会按上面给出的顺序，依次介绍这些密码学概念以及如何在日常开发中使用它们。

不过在开始学习之前，我们先来了解一下什么是密码学，以及密码学的几大用途。

1、什么是密码学

密码学（Cryptography）是提供信息安全和保护的科学。它在我们的数字世界中无处不在，当你打开网站时、发送电子邮件时、连接到 WiFi 网络时，使用账号密码登录 APP 时、使用二步认证验证码认证身份时，都有涉及到密码学相关技术。因此开发人员应该对密码学有基本的了解，以避免写出不安全的代码。至少也得知道如何使用密码算法和密码库，了解哈希、对称密码算法、非对称密码算法（cipher）与加密方案这些概念，知晓数字签名及其背后的密码系统和算法。

2、密码学的用途

1. 加密与密钥

密码学的一大用途，就是进行数据的安全存储和安全传输。这可能涉及使用对称或非对称加密方案加密和解密数据，其中一个或多个密钥用于将数据从明文转换为加密形式或者相反。

对称加密（如 AES、Twofish 和 ChaCha20）使用相同的密钥（一个密钥）来加密和解密消息，而非对称加密使用公钥密码系统（如 RSA 或 ECC）和密钥对（两个密钥）来进行这两项操作。

单纯使用加密算法是不够的，这是因为有的加密算法只能按块进行加密，而且很多加密算法并不能保证密文的真实性、完整性。因此现实中我们通常会使用加密方案进行数据的加密解密。加密方案是结合了加密算法、消息认证或数字签名算法、块密码模式等多种算法，能同时保证数据的安全性、真实性、完整性的一套加密方案，如 AES-256-CTR-HMAC-SHA-256、ChaCha20-Poly1305 或 ECIES-secp256k1-AES-128-GCM。后面我们会学到，加密方案的名称就是使用到的各种密码算法名称的组合。

2. 数字签名与消息认证

密码学提供了保证消息真实性（authenticity）、完整性（integrity）和不可否认性（non-repudiation）的方法：数字签名算法与消息认证（MAC）算法。

大多数数字签名算法（如 DSA、ECDSA 和 EdDSA）使用非对称密钥对（私钥和公钥）干这个活：消息由私钥签名，签名由相应的公钥验证。在银行系统中，数字签名用于签署和批准付款。在区块链签名交易中，用户可以将区块链资产从一个地址转移到另一个地址，确保转移操作的真实、完整、不可否认。

消息认证算法（如 HMAC）和消息认证码（MAC 码）也是密码学的一部分。MAC 跟数字签名的功能实际上是一致的，区别在于 MAC 使用哈希算法或者对称加密系统。

3. 安全随机数

密码学的另一个部分，是熵（entropy，不可预测的随机性）和随机数的安全生成（例如使用 CSPRNG）。

安全随机数理论上是不可预测的，开发人员需要关心的是你使用的随机数生成器是否足够安全。很多编程语言中被广泛使用的随机数生成器都是不安全的（比如 Python 的 random 库），如果你在对安全有严格要求的场景下使用了这种不安全的随机生成器，可能会黑客被预测到它生成的随机数，导致系统或者 APP 被黑客入侵。

4. 密钥交换

密码学定义了密钥交换算法（如 Diffie-Hellman 密钥交换和 ECDH）和密钥构建方案，用于在需要安全传输消息的两方之间安全地构建加密密钥。这种算法通常在两方之间建立新的安全连接时执行，例如当你打开一个现代 HTTPS 网站或连接到 WiFi 网络时。

5. 加密哈希与 Password 哈希

密码学提供了加密哈希函数（如 SHA-3 和 BLAKE2）将消息转换为消息摘要/数字指纹（固定长度的散列），确保无法逆向出原始消息，并且几乎不可能找到具有相同哈希值的两条不同消息。

例如，在区块链系统中，哈希用于生成区块链地址、交易 ID 以及许多其他算法和协议。在 Git 中，加密哈希用于为文件和提交生成唯一 ID。

而密钥派生函数（如 Scrypt 和 Argon2）通过从基于文本的 Password 安全地派生出哈希值（或密钥），并且这种算法还通过注入随机参数（盐）和使用大量迭代和计算资源使密码破解速度变慢。

密码学也被用于密钥（一个非常大的、保密的数字）的生成。因为人类只擅长记忆字符形式的 Password/Passphrases，而各种需要加密算法需要的密钥，都是一个非常大的、保密的数字。

3、混淆与扩散

在密码学当中，香农提出的混淆（confusion）与扩散（diffusion）是设计安全密码学算法的两个原则。

混淆使密文和对称加密中密钥的映射关系变得尽可能的复杂，使之难以分析。如果使用了混淆，那么输出密文中的每个比特位都应该依赖于密钥和输入数据的多个部分，确保两者无法建立直接映射。混淆常用的方法是「替换」与「排列」。

「扩散」将明文的统计结构扩散到大量密文中，隐藏明文与密文之间的统计学关系。使单个明文或密钥位的影响尽可能扩大到更多的密文中去，确保改变输入中的任意一位都应该导致输出中大约一半的位发生变化，反过来改变输出密文的任一位，明文中大约一半的位也必须发生变化。扩散常用的方法是「置换」。

这两个原则被包含在大多数散列函数、MAC 算法、随机数生成器、对称和非对称密码算法中。

4、密码库

说了这么多，作为一个程序员，我学习密码学的目的，只是了解如何在编程语言中使用现代密码库，并从中挑选合适的算法、使用合适的参数。

程序员经常会自嘲日常复制粘贴，但是在编写涉及到密码学的代码时，一定要谨慎处理！盲目地从 Internet 复制/粘贴代码或遵循博客中的示例可能会导致安全问题；曾经安全的代码、算法或者最佳实践，随着时间的推移也可能变得不再安全。

二、哈希函数

哈希函数，或者叫散列函数，是一种从任何一种数据中创建一个数字指纹（也叫数字摘要）的方法，散列函数把数据压缩（或者放大）成一个长度固定的字符串。

哈希函数的输入空间（文本或者二进制数据）是无限大，但是输出空间（一个固定长度的摘要）却是有限的。将「无限」映射到「有限」，不可避免的会有概率不同的输入得到相同的输出，这种情况我们称为碰撞（collision）。

一个简单的哈希函数是直接对输入数据/文本的字节求和。它会导致大量的碰撞，例如 hello 和 ehllo 将具有相同的哈希值。

更好的哈希函数可以使用这样的方案：它将第一个字节作为状态，然后转换状态（例如，将它乘以像 31 这样的素数），然后将下一个字节添加到状态，然后再次转换状态并添加下一个字节等。这样的操作可以显着降低碰撞概率并产生更均匀的分布。

1、加密哈希函数

加密哈希函数（也叫密码学哈希函数）是指一类有特殊属性的哈希函数。

一个好的「加密哈希函数」必须满足抗碰撞（collision-resistant）和不可逆（irreversible）这两个条件。抗碰撞是指通过统计学方法（彩虹表）很难或几乎不可能猜出哈希值对应的原始数据，而不可逆则是说攻击者很难或几乎不可能从算法层面通过哈希值逆向演算出原始数据。

具体而言，一个理想的加密哈希函数，应当具有如下属性：

快速：计算速度要足够快
确定性：对同样的输入，应该总是产生同样的输出
难以分析：对输入的任何微小改动，都应该使输出完全发生变化
不可逆：从其哈希值逆向演算出输入值应该是不可行的。这意味着没有比暴力破解更好的破解方法
无碰撞：找到具有相同哈希值的两条不同消息应该非常困难（或几乎不可能）

现代加密哈希函数（如 SHA2 和 SHA3）都具有上述几个属性，并被广泛应用在多个领域，各种现代编程语言和平台的标准库中基本都包含这些常用的哈希函数。

2、量子安全性

现代密码学哈希函数（如 SHA2, SHA3, BLAKE2）都被认为是量子安全的，无惧量子计算机的发展。

3、加密哈希函数的应用

1. 数据完整性校验

加密哈希函数被广泛用于文件完整性校验。如果你从网上下载的文件计算出的 SHA256 校验和（checksum）跟官方公布的一致，那就说明文件没有损坏。

但是哈希函数自身不能保证文件的真实性，目前来讲，真实性通常是 TLS 协议要保证的，它确保你在 openssl 网站上看到的「SHA256 校验和」真实无误（未被篡改）。

现代网络基本都很难遇到文件损坏的情况了，但是在古早的低速网络中，即使 TCP 跟底层协议已经有多种数据纠错手段，下载完成的文件仍然是有可能损坏的。这也是以前 rar 压缩格式很流行的原因之一—— rar 压缩文件拥有一定程度上的自我修复能力，传输过程中损坏少量数据，仍然能正常解压。

2. 保存密码

加密哈希函数还被用于密码的安全存储，现代系统使用专门设计的安全哈希算法计算用户密码的哈希摘要，保存到数据库中，这样能确保密码的安全性。除了用户自己，没有人清楚该密码的原始数据，即使数据库管理员也只能看到一个哈希摘要。

3. 生成唯一ID

加密哈希函数也被用于为文档或消息生成（绝大多数情况下）唯一的 ID，因此哈希值也被称为数字指纹。

注意这里说的是数字指纹，而非数字签名。数字签名是与下一篇文章介绍的「MAC」码比较类似的，用于验证消息的真实、完整、认证作者身份的一段数据。

加密哈希函数计算出的哈希值理论上确实有碰撞的概率，但是这个概率实在太小了，因此绝大多数系统（如 Git）都假设哈希函数是无碰撞的（collistion free）。

文档的哈希值可以被用于证明该文档的存在性，或者被当成一个索引，用于从存储系统中提取文档。

使用哈希值作为唯一 ID 的典型例子，Git 版本控制系统（如 3c3be25bc1757ca99aba55d4157596a8ea217698）肯定算一个，比特币地址（如 1BvBMSEYstWetqTFn5Au4m4GFg7xJaNVN2）也算。

4. 伪随机数生成

哈希值可以被当作一个随机数看待，生成一个伪随机数的简单流程如下：

通过随机事件得到一个熵（例如键盘点击或鼠标移动），将它作为最初的随机数种子（random seed）。
添加一个 1 到熵中，进行哈希计算得到第一个随机数
再添加一个 2，进行哈希计算得到第二个随机数
以此类推

当然为了确保安全性，实际的加密随机数生成器会比这再复杂一些

4、安全的加密哈希算法

1. SHA-2, SHA-256, SHA-512

SHA-2，即 Secure Hash Algorithm 2，是一组强密码哈希函数，其成本包括：SHA-256（256位哈希）、SHA-384（384位哈希）、SHA-512（512位哈希）等。基于密码概念「Merkle–Damgård 构造」，目前被认为高度安全。 SHA-2 是 SHA-1 的继任者，于 2001 年在美国作为官方加密标准发布。

SHA-2 在软件开发和密码学中被广泛使用，可用于现代商业应用。其中 SHA-256 被广泛用于 HTTPS 协议、文件完整性校验、比特币区块链等各种场景。

Python 代码示例：

import hashlib, binascii

text = 'hello'
data = text.encode("utf8")

sha256hash = hashlib.sha256(data).digest()
print(f"SHA-256({text}) = ", binascii.hexlify(sha256hash).decode("utf8"))

sha384hash = hashlib.sha384(data).digest()
print(f"SHA-384({text}) = ", binascii.hexlify(sha384hash).decode("utf8"))

sha512hash = hashlib.sha512(data).digest()
print(f"SHA-512({text}) = ", binascii.hexlify(sha512hash).decode("utf8"))

输出如下：

SHA-256('hello') = 2cf24dba5fb0a30e26e83b2ac5b9e29e1b161e5c1fa7425e73043362938b9824
SHA-384('hello') = 59e1748777448c69de6b800d7a33bbfb9ff1b463e44354c3553bcdb9c666fa90125a3c79f90397bdf5f6a13de828684f
SHA-512('hello') = 9b71d224bd62f3785d96d46ad3ea3d73319bfbc2890caadae2dff72519673ca72323c3d99ba5c11d7c7acc6e14b8c5da0c4663475c2e5c3adef46f73bcdec043

2. 更长的哈希值 == 更高的抗碰撞能力

按照设计，哈希函数的输出越长，就有望实现更高的安全性和抗碰撞能力（但也有一些例外）。一般来说，128 位哈希算法比 256 位哈希算法弱，256 位哈希算法比 512 位哈希算法弱。

因此显然 SHA-512 比 SHA-256 更强。我们可以预期，SHA-512 的碰撞概率要比 SHA-256 更低。

3. SHA-3, SHA3-256, SHA3-512, Keccak-256

在输出的哈希长度相同时，SHA-3（及其变体 SHA3-224、SHA3-256、SHA3-384、SHA3-512）被认为拥有比 SHA-2（SHA-224、SHA-256、SHA-384、SHA-512）更高的加密强度。例如，对于相同的哈希长度（256 位），SHA3-256 提供比 SHA-256 更高的加密强度。

SHA-3 系列函数是 Keccak 哈希家族的代表，它基于密码学概念海绵函数。而 Keccak 是SHA3 NIST 比赛的冠军。

与 SHA-2 不同，SHA-3 系列加密哈希函数不易受到长度拓展攻击 Length extension attack.

SHA-3 被认为是高度安全的，并于 2015 年作为美国官方推荐的加密标准发布。

以太坊（Ethereum）区块链中使用的哈希函数 Keccak-256 是 SHA3-256 的变体，在代码中更改了一些常量。

哈希函数 SHAKE128(msg, length) 和 SHAKE256(msg, length) 是 SHA3-256 和 SHA3-512 算法的变体，它们输出消息的长度可以变化。

SHA3 的 Python 代码示例：

import hashlib, binascii

text = 'hello'
data = text.encode("utf8")

sha3_256hash = hashlib.sha3_256(data).digest()
print(f"SHA3-256({text}) = ", binascii.hexlify(sha3_256hash).decode("utf8"))

sha3_512hash = hashlib.sha3_512(data).digest()
print(f"SHA3-512({text}) = ", binascii.hexlify(sha3_512hash).decode("utf8"))

输出：

SHA3-256('hello') = 3338be694f50c5f338814986cdf0686453a888b84f424d792af4b9202398f392
Keccak-256('hello') = 1c8aff950685c2ed4bc3174f3472287b56d9517b9c948127319a09a7a36deac8
SHA3-512('hello') = 75d527c368f2efe848ecf6b073a36767800805e9eef2b1857d5f984f036eb6df891d75f72d9b154518c1cd58835286d1da9a38deba3de98b5a53e5ed78a84976

SHAKE-128('hello', 256) = 4a361de3a0e980a55388df742e9b314bd69d918260d9247768d0221df5262380
SHAKE-256('hello', 160) = 1234075ae4a1e77316cf2d8000974581a343b9eb

4. BLAKE2 / BLAKE2s / BLAKE2b

BLAKE / BLAKE2 / BLAKE2s / BLAKE2b 是一系列快速、高度安全的密码学哈希函数，提供 160 位、224 位、256 位、384 位和 512 位摘要大小的计算，在现代密码学中被广泛应用。BLAKE 进入了SHA3 NIST 比赛的决赛。

BLAKE2 函数是 BLAKE 的改进版本。
BLAKE2s（通常为 256 位）是 BLAKE2 实现，针对 32 位微处理器进行了性能优化。
BLAKE2b（通常为 512 位）是 BLAKE2 实现，针对 64 位微处理器进行了性能优化。

BLAKE2 哈希函数具有与 SHA-3 类似的安全强度，但开发人员目前仍然更倾向于使用 SHA2 和 SHA3。

BLAKE 哈希值的 Python 示例：

import hashlib, binascii

text = 'hello'
data = text.encode("utf8")

blake2s = hashlib.new('blake2s', data).digest()
print("BLAKE2s({text}) = ", binascii.hexlify(blake2s).decode("utf-8"))

blake2b = hashlib.new('blake2b', data).digest()
print("BLAKE2b({text}) = ", binascii.hexlify(blake2b).decode("utf-8"))

输出如下：

BLAKE2s('hello') = 19213bacc58dee6dbde3ceb9a47cbb330b3d86f8cca8997eb00be456f140ca25
BLAKE2b('hello') = e4cfa39a3d37be31c59609e807970799caa68a19bfaa15135f165085e01d41a65ba1e1b146aeb6bd0092b49eac214c103ccfa3a365954bbbe52f74a2b3620c94

5. RIPEMD-160

RIPEMD-160, RIPE Message Digest 是一种安全哈希函数，发布于 1996 年，目前主要被应用在 PGP 和比特币中。

RIPEMD 的 160 位变体在实践中被广泛使用，而 RIPEMD-128、RIPEMD-256 和 RIPEMD-320 等其他变体并不流行，并且它们的安全优势具有争议。

建议优先使用 SHA-2 和 SHA-3 而不是 RIPEMD，因为它们输出的哈希值更长，抗碰撞能力更强。

Python 示例：

import hashlib, binascii

text = 'hello'
data = text.encode("utf8")

ripemd160 = hashlib.new('ripemd160', data).digest()
print("RIPEMD-160({text}) = ", binascii.hexlify(ripemd160).decode("utf-8"))

# => RIPEMD-160({text}) =  108f07b8382412612c048d07d13f814118445acd

6. 其他安全哈希算法

以下是目前流行的强加密哈希函数，它们都可被用于替代 SHA-2、SHA-3 和 BLAKE2：

Whirlpool 发布于 2000 年，此算法输出固定的 512 位哈希值。该算法使用512位的密钥，参考了分组密码的思路，使用轮函数加迭代，算法结构与 AES 相似。
SM3 是中国国密密码杂凑算法标准，由国家密码管理局于 2010 年 12 月公布。它类似于 SHA-256（基于 Merkle-Damgård 结构），输出为 256 位哈希值。
GOST（GOST R 34.11-94）哈希函数是俄罗斯的国家标准，它的输出也是 256 位哈希值。

以下函数是 SHA-2、SHA-3 和 BLAKE 的不太受欢迎的替代品，它们是SHA3 NIST 比赛的决赛入围者

Skein 能够计算出 128、160、224、256、384、512 和 1024 位哈希值。
Grøstl 能够计算出 224、256、384 和 512 位哈希值。
JH 能够计算出 224、256、384 和 512 位哈希值。

5、不安全的加密哈希算法

一些老一代的加密哈希算法，如 MD5, SHA-0 和 SHA-1 被认为是不安全的，并且都存在已被发现的加密漏洞（碰撞）。不要使用 MD5、SHA-0 和 SHA-1！这些哈希函数都已被证明不够安全。

使用这些不安全的哈希算法，可能会导致数字签名被伪造、密码泄漏等严重问题！

另外也请避免使用以下被认为不安全或安全性有争议的哈希算法： MD2, MD4, MD5, SHA-0, SHA-1, Panama, HAVAL（有争议的安全性，在 HAVAL-128 上发现了碰撞），Tiger（有争议，已发现其弱点），SipHash（它属于非加密哈希函数）。

6、PoW 工作量证明哈希函数

区块链中的 Proof-of-Work 工作量证明挖矿算法使用了一类特殊的哈希函数，这些函数是计算密集型和内存密集型的。这些哈希函数被设计成需要消耗大量计算资源和大量内存，并且很难在硬件设备（例如集成电路或矿机）中实现，也就难以设计专用硬件来加速计算。这种哈希函数被称为抗 ASIC（ASIC-resistant）。

大部分工作量证明（Proof-of-Work）算法，都是要求计算出一个比特定值（称为挖掘难度）更大的哈希值。因为哈希值是不可预测的，为了找出符合条件的哈希值，矿工需要计算数十亿个不同的哈希值，再从中找出最大的那个。比如，一个工作量证明问题可能会被定义成这样：已有常数 x，要求找到一个数 p，使 hash(x + p) 的前十个比特都为 0.

有许多哈希函数是专为工作量证明挖掘算法设计的，例如 ETHash、Equihash、CryptoNight 和 Cookoo Cycle. 这些哈希函数的计算速度很慢，通常使用 GPU 硬件（如 NVIDIA GTX 1080 等显卡）或强大的 CPU 硬件（如 Intel Core i7-8700K）和大量快速 RAM 内存（如 DDR4 芯片）来执行这类算法。这些挖矿算法的目标是通过刺激小型矿工（家庭用户和小型矿场）来最大限度地减少挖矿的集中化，并限制挖矿行业中高级玩家们（他们有能力建造巨型挖矿设施和数据中心）的力量。与少数的高玩相比，大量小玩家意味着更好的去中心化。

目前大型虚拟货币挖矿公司手中的主要武器是 ASIC 矿机，因此，现代加密货币通常会要求使用「抗 ASIC 哈希算法」或「权益证明（proof-of-stake）共识协议」进行「工作量证明挖矿」，以限制这部分高级玩家，达成更好的去中心化。

因为工作量证明算法需要消耗大量能源，不够环保，以太坊等区块链已经声明未来将会升级到权益证明（Proof-of-S）这类更环保的算法。

1. ETHash

这里简要说明下以太坊区块链中使用的 ETHash 工作量证明挖掘哈希函数背后的思想。

ETHash 是以太坊区块链中的工作量证明哈希函数。它是内存密集型哈希函数（需要大量 RAM 才能快速计算），因此它被认为是抗 ASIC 的。

ETHash 的工作流程：

基于直到当前区块的整个链，为每个区块计算一个「种子」
从种子中计算出一个 16 MB 的伪随机缓存
从缓存中提取 1 GB 数据集以用于挖掘
挖掘涉及将数据集的随机切片一起进行哈希

2. Equihash

简要解释一下 Zcash、Bitcoin Gold 和其他一些区块链中使用的 Equihash 工作量证明挖掘哈希函数背后的思想。

Equihash 是 Zcash 和 Bitcoin Gold 区块链中的工作量证明哈希函数。它是内存密集型哈希函数（需要大量 RAM 才能进行快速计算），因此它被认为是抗 ASIC 的。

Equihash 的工作流程：

基于直到当前区块的整个链，使用 BLAKE2b 计算出 50 MB 哈希数据集
在生成的哈希数据集上解决「广义生日问题」（从 2097152 中挑选 512 个不同的字符串，使得它们的二进制 XOR 为零）。已知最佳的解决方案（瓦格纳算法）在指数时间内运行，因此它需要大量的内存密集型和计算密集型计算
对前面得到的结果，进行双 SHA256 计算得到最终结果，即 SHA256(SHA256(solution))

更多信息参见 GitHub - tromp/equihash: multi-parameter Equihash proof-of-work multi-threaded C solvers

7、非加密哈希函数

加密哈希函数非常看重「加密」，为了实现更高的安全强度，费了非常多的心思、也付出了很多代价。

但是实际应用中很多场景是不需要这么高的安全性的，相反可能会对速度、随机均匀性等有更高的要求。这就催生出了很多「非加密哈希函数」。

非加密哈希函数的应用场景有很多：

哈希表 Hash Table: 在很多语言中也被称为 map/dict，它使用的算法很简单，通常就是把对象的各种属性不断乘个质数（比如 31）再相加，哈希空间会随着表的变化而变化。这里最希望的是数据的分布足够均匀。
一致性哈希：目的是解决分布式缓存的问题。在移除或者添加一个服务器时，能够尽可能小地改变已存在的服务请求与处理请求服务器之间的映射关系。
高性能哈希算法：SipHash MurMurHash3 等，使用它们的目的可能是对数据进行快速去重，要求就是足够快。

有时我们甚至可能不太在意哈希碰撞的概率。也有的场景输入是有限的，这时我们可能会希望哈希函数具有可逆性。

总之非加密哈希函数也有非常多的应用，但不是本文的主题。这里就不详细介绍了，有兴趣的朋友们可以自行寻找其他资源。

三、MAC与密钥派生函数KDF

1、MAC 消息认证码

MAC 消息认证码，即 Message Authentication Code，是用于验证消息的一小段信息。换句话说，能用它确认消息的真实性——消息来自指定的发件人并且没有被篡改。

MAC 值通过允许验证者（也拥有密钥）检测消息内容的任何更改来保护消息的数据完整性及其真实性。

一个安全的 MAC 函数，跟加密哈希函数非常类似，也拥有如下特性：

快速：计算速度要足够快
确定性：对同样的消息跟密钥，应该总是产生同样的输出
难以分析：对消息或密钥的任何微小改动，都应该使输出完全发生变化
不可逆：从 MAC 值逆向演算出消息跟密钥应该是不可行的。
无碰撞：找到具有相同哈希的两条不同消息应该非常困难（或几乎不可能）

但是 MAC 算法比加密哈希函数多一个输入值：密钥，因此也被称为 keyed hash functions，即「加密钥的哈希函数」。

如下 Python 代码使用 key 跟消息计算出对应的 HMAC-SHA256 值：

import hashlib, hmac, binascii

key = b"key"
msg = b"some msg"

mac = hmac.new(key, msg, hashlib.sha256).digest()

print(f"HMAC-SHA256({key}, {msg})", binascii.hexlify(mac).decode('utf8'))

# => HMAC-SHA256(b'key', b'some msg') = 32885b49c8a1009e6d66662f8462e7dd5df769a7b725d1d546574e6d5d6e76ad

HMAC 的算法实际上非常简单，参考 wiki/HMAC 给出的伪码，编写了下面这个 Python 实现，没几行代码，但是完全 work：

import hashlib, binascii

def xor_bytes(b1, b2):
  return bytes(a ^ c for a, c in zip(b1, b2))

def my_hmac(key, msg, hash_name):
  # hash => (block_size, output_size)
  # 单位是 bytes，数据来源于 https://en.wikipedia.org/wiki/HMAC
  hash_size_dict = {
    "md5": (64, 16),
    "sha1": (64, 20),
    "sha224": (64, 28),
    "sha256": (64, 32),
    # "sha512/224": (128, 28),  # 这俩算法暂时不清楚在 hashlib 里叫啥名
    # "sha512/256": (128, 32),
    "sha_384": (128, 48),
    "sha_512": (128, 64),
    "sha3_224": (144, 28),
    "sha3_256": (136, 32),
    "sha3_384": (104, 48),
    "sha3_512": (72, 64),
  }
  if hash_name not in hash_size_dict:
    raise ValueError("unknown hash_name")

  block_size, output_size = hash_size_dict[hash_name]
  hash_ = getattr(hashlib, hash_name)

  # 确保 key 的长度为 block_size
  block_sized_key = key
  if len(key) > block_size:
    block_sized_key = hash_(key).digest()  # 用 hash 函数进行压缩
  if len(key) < block_size:
    block_sized_key += b'\x00' * (block_size - len(key))  # 末尾补 0
  
  o_key_pad = xor_bytes(block_sized_key, (b"\x5c" * block_size))  # Outer padded key
  i_key_pad = xor_bytes(block_sized_key, (b"\x36" * block_size))  # Inner padded key

  return hash_(o_key_pad + hash_(i_key_pad + msg).digest()).digest()


# 下面验证下
key = b"key"
msg = b"some msg"

mac_ = my_hmac(key, msg, "sha256")
print(f"HMAC-SHA256({key}, {msg})", binascii.hexlify(mac_).decode('utf8'))

# 输出跟标准库完全一致：
# => HMAC-SHA256(b'key', b'some msg') = 32885b49c8a1009e6d66662f8462e7dd5df769a7b725d1d546574e6d5d6e76ad

2、MAC 与哈希函数、数字签名的区别

上一篇文章提到过，哈希函数只负责生成哈希值，不负责哈希值的可靠传递。

而数字签名呢，跟 MAC 非常相似，但是数字签名使用的是非对称加密系统，更复杂，计算速度也更慢。

MAC 的功能跟数字签名一致，都是验证消息的真实性（authenticity）、完整性（integrity）、不可否认性（non-repudiation），但是 MAC 使用哈希函数或者对称密码系统来做这件事情，速度要更快，算法也更简单。

3、MAC 的应用

1. 验证消息的真实性、完整性

这是最简单的一个应用场景，在通信双向都持有一个预共享密钥的前提下，通信时都附带上消息的 MAC 码。接收方也使用「收到的消息+预共享密钥」计算出 MAC 码，如果跟收到的一致，就说明消息真实无误。

注意这种应用场景中，消息是不保密的！

2. AE 认证加密 - Authenticated encryption

常用的加密方法只能保证数据的保密性，并不能保证数据的完整性。

而这里介绍的 MAC 算法，或者还未介绍的基于非对称加密的数字签名，都只能保证数据的真实性、完整性，不能保证数据被安全传输。

而认证加密，就是将加密算法与 MAC 算法结合使用的一种加密方案。

在确保 MAC 码「强不可伪造」的前提下，首先对数据进行加密，然后计算密文的 MAC 码，再同时传输密文与 MAC 码，就能同时保证数据的保密性、完整性、真实性，这种方法叫 Encrypt-then-MAC, 缩写做 EtM. 接收方在解密前先计算密文的 MAC 码与收到的对比，就能验证密文的完整性与真实性。

AE 有一种更安全的变体——带有关联数据的认证加密 (authenticated encryption with associated data，AEAD)。 AEAD 将「关联数据(Associated Data, AD)」——也称为「附加验证数据（Additional Authenticated Data, AAD）」——绑定到密文和它应该出现的上下文，以便可以检测和拒绝将有效密文“剪切并粘贴”到不同上下文的尝试。 AEAD 用于加密和未加密数据一起使用的场景（例如，在加密的网络协议中），并确保整个数据流经过身份验证和完整性保护。换句话说，AEAD 增加了检查某些内容的完整性和真实性的能力。

我们会在第六章「对称加密算法」中看到如何通过 Python 使用 AEAD 加密方案 AES-256-GCM.

3. 基于 MAC 的伪随机数生成器

MAC 码的另一个用途就是伪随机数生成函数，相比直接使用熵+哈希函数的进行伪随机数计算，MAC 码因为多引入了一个变量 key，理论上它会更安全。

这种场景下，我们称 MAC 使用的密钥为 salt，即盐。

next_seed = MAC(salt, seed)

4、KDF 密钥派生函数

我们都更喜欢使用密码来保护自己的数据而不是二进制的密钥，因为相比之下二进制密钥太难记忆了，字符形式的密码才是符合人类思维习惯的东西。

可对计算机而言就刚好相反了，现代密码学的很多算法都要求输入是一个大的数字，二进制的密钥就是这样一个大的数字。因此显然我们需要一个将字符密码（Password）转换成密钥（Key）的函数，这就是密钥派生函数 Key Derivation Function.

直接使用 SHA256 之类的加密哈希函数来生成密钥是不安全的，因为为了方便记忆，通常密码并不会很长，绝大多数人的密码长度估计都不超过 15 位。甚至很多人都在使用非常常见的弱密码，如 123456 admin 生日等等。这就导致如果直接使用 SHA256 之类的算法，许多密码将很容易被暴力破解、字典攻击、彩虹表攻击等手段猜测出来！

KDF 目前主要从如下三个维度提升 hash 碰撞难度：

时间复杂度：对应 CPU/GPU 计算资源
空间复杂度：对应 Memory 内存资源
并行维度：使用无法分解的算法，锁定只允许单线程运算

主要手段是加盐，以及多次迭代。这种设计方法被称为「密钥拉伸 Key stretching」。

因为它的独特属性，KDF 也被称作慢哈希算法。

目前比较著名的 KDF 算法主要有如下几个：

PBKDF2：这是一个非常简单的加密 KDF 算法，目前已经不推荐使用。
Bcrypt：安全性在下降，用得越来越少了。不建议使用。
Scrypt：可以灵活地设定使用的内存大小，在 argon2 不可用时，可使用它。
Argon2：目前最强的密码 Hash 算法，在 2015 年赢得了密码 Hash 竞赛。

如果你正在开发一个新的程序，需要使用到 KDF，建议选用 argon2/scrypt.

Python 中最流行的密码学库是 cryptography，requests 的底层曾经就使用了它（新版本已经换成使用标准库 ssl 了），下面我们使用这个库来演示下 Scrypt 算法的使用：

# pip install cryptography==36.0.1
import os
from cryptography.hazmat.primitives.kdf.scrypt import Scrypt

salt = os.urandom(16)

# derive
kdf = Scrypt(
    salt=salt,
    length=32,
    n=2**14,
    r=8,
    p=1,
)
key = kdf.derive(b"my great password")

# verify
kdf = Scrypt(
    salt=salt,
    length=32,
    n=2**14,
    r=8,
    p=1,
)
kdf.verify(b"my great password", key)

四、安全随机数生成器 CSPRNG

在密码学中，随机性（熵）扮演了一个非常重要的角色，许多密码学算法都要求使用一个不可预测的随机数，只有在生成的随机数不可预测时，这些算法才能保证其安全性。

比如 MAC 算法中的 key 就必须是一个不可预测的值，在这个条件下 MAC 值才是不可伪造的。

另外许多的高性能算法如快速排序、布隆过滤器、蒙特卡洛方法等，都依赖于随机性，如果随机性可以被预测，或者能够找到特定的输入值使这些算法变得特别慢，那黑客就能借此对服务进行 DDoS 攻击，以很小的成本达到让服务不可用的目的。

1、PRNG 伪随机数生成器

Pseudo-Random Number Generators(PRNG) 是一种数字序列的生成算法，它生成出的数字序列的统计学属性跟真正的随机数序列非常相似，但它生成的伪随机数序列并不是真正的随机数序列！因为该序列完全依赖于提供给 PRNG 的初始值，这个值被称为 PRNG 的种子。

算法流程如下，算法的每次迭代都生成出一个新的伪随机数：

如果输入的初始种子是相同的，PRNG 总是会生成出相同的伪随机数序列，因此 PRNG 也被称为 Deterministic Random Bit Generator (DRBG)，即确定性随机比特生成器。

实际上目前也有所谓的「硬件随机数生成器 TRNG」能生成出真正的随机数，但是因为 PRNG 的高速、低成本、可复现等原因，它仍然被大量使用在现代软件开发中。

PRNG 可用于从一个很小的初始随机性（熵）生成出大量的伪随机性，这被称做「拉伸（Stretching）」。

PRNG 被广泛应用在前面提到的各种依赖随机性的高性能算法以及密码学算法中。

2、PRNG 的实现

我们在上一篇文章的「MAC 的应用」一节中提到，一个最简单的 PRNG 可以直接使用 MAC 算法实现，用 Python 实现如下：

import hmac, hashlib
def random_number_generator(seed: bytes, max_num: int):
  state = seed
  counter = 0

  while True:
    state = hmac.new(state, bytes(counter), hashlib.sha1).digest()    
    counter += 1

    # 这里取余实际上是压缩了信息，某种程度上说，这可以保证内部的真实状态 state 不被逆向出来
    yield int.from_bytes(state, byteorder="big") % max_num

# 测试下，计算 20 个 100 以内的随机数
gen = random_number_generator(b"abc", 100)
print([next(gen) for _ in range(20)])
# => [71, 41, 52, 18, 51, 14, 58, 30, 70, 20, 59, 93, 3, 10, 81, 63, 48, 67, 18, 36]

3、随机性 - 熵

如果初始的 PRNG 种子是完全不可预测的，PRNG 就能保证整个随机序列都不可预测。

因此在 PRNG 中，生成出一个足够随机的种子，就变得非常重要了。

一个最简单的方法，就是收集随机性。对于桌面电脑，随机性可以从鼠标的移动点击、按键事件、网络状况等随机输入来收集。这个事情是由操作系统在内核中处理的，内核会直接为应用程序提供随机数获取的 API，比如 Linux/MacOSX 的 /dev/random 虚拟设备。

如果这个熵的生成有漏洞，就很可能造成严重的问题，一个现实事件就是安卓的 java.security.SecureRandom 漏洞导致安卓用户的比特币钱包失窃。

Python 的 random 库的默认会使用当前时间作为初始 seed，这显然是不够安全的——黑客如果知道你运行程序的大概时间，就能通过遍历的方式暴力破解出你的随机数来！

4、CSPRNG 密码学安全随机数生成器

Cryptography Secure Random Number Generators(CSPRNG) 是一种适用于密码学领域的 PRNG，一个 PRNG 如果能够具备如下两个条件，它就是一个 CSPRNG:

能通过「下一比特测试 next-bit test」：即使有人获知了该 PRNG 的 k 位，他也无法使用合理的资源预测第 k+1 位的值
如果攻击者猜出了 PRNG 的内部状态或该状态因某种原因而泄漏，攻击者也无法重建出内部状态泄漏之前生成的所有随机数

有许多的设计都被证明可以用于构造一个 CSPRNG:

基于计数器(CTR)模式下的安全分组密码、流密码或安全散列函数的 CSPRNG
基于数论设计的 CSPRNG，它依靠整数分解问题（IFP）、离散对数问题（DLP）或椭圆曲线离散对数问题（ECDLP）的高难度来确保安全性
CSPRNG 基于加密安全随机性的特殊设计，例如 Yarrow algorithm 和 Fortuna，这俩分别被用于 MacOS 和 FreeBSD.

大多数的 CSPRNG 结合使用来自 OS 的熵与高质量的 PRNG，并且一旦系统生成了新的熵（这可能来自用户输入、磁盘 IO、系统中断、或者硬件 RNG），CSPRNG 会立即使用新的熵来作为 PRNG 新的种子。这种不断重置 PRNG 种子的行为，使随机数变得非常难以预测。

CSPRNG 的用途

加密程序：因为 OS 中熵的收集很缓慢，等待收集到足够多的熵再进行运算是不切实际的，因此很多的加密程序都使用 CSPRNG 来从系统的初始熵生成出足够多的伪随机熵。
其他需要安全随机数的场景 emmmm

5、如何在代码中使用 CSPRNG

多数系统都内置了 CSPRNG 算法并提供了内核 API，Unix-like 系统都通过如下两个虚拟设备提供 CSPRNG:

/dev/random（受限阻塞随机生成器）: 从这个设备中读取到的是内核熵池中已经收集好的熵，如果熵池空了，此设备会一直阻塞，直到收集到新的环境噪声。
/dev/urandom（不受限非阻塞随机生成器）: 它可能会返回内核熵池中的熵，也可能返回使用「之前收集的熵 + CSPRNG」计算出的安全伪随机数。它不会阻塞。

编程语言的 CSPRNG 接口或库如下：

Java: java.security.SecureRandom
Python: secrets 库或者 os.urandom()
C#: System.Security.Cryptography.RandomNumberGenerator.Create()
JavaScript: 客户端可使用 window.crypto.getRandomValues(Uint8Array)，服务端可使用 crypto.randomBytes()

比如使用 Python 实现一个简单但足够安全的随机密码生成器：

import secrets
import string

chars = string.digits + "your_custom_-content" +  string.ascii_letters
def random_string(length: int):
    """生成随机字符串"""
    # 注意，这里不应该使用 random 库！而应该使用 secrets
    code = "".join(secrets.choice(chars) for _ in range(length))
    return code

random_string(24)
# => _rebBfgYs4OtkrPbYtnGmc4n

五、密钥交换 DHKE 与完美前向保密 PFS

在密码学中密钥交换是一种协议，功能是在两方之间安全地交换加密密钥，其他任何人都无法获得密钥的副本。通常各种加密通讯协议的第一步都是密钥交换。密钥交换技术具体来说有两种方案：

密钥协商：协议中的双方都参与了共享密钥的生成，两个代表算法是 Diffie-Hellman (DHKE) 和 Elliptic-Curve Diffie-Hellman (ECDH)
密钥传输：双方中其中一方生成出共享密钥，并通过此方案将共享密钥传输给另一方。密钥传输方案通常都通过公钥密码系统实现。比如在 RSA 密钥交换中，客户端使用它的私钥加密一个随机生成的会话密钥，然后将密文发送给服务端，服务端再使用它的公钥解密出会话密钥。

密钥交换协议无时无刻不在数字世界中运行，在你连接 WiFi 时，或者使用 HTTPS 协议访问一个网站，都会执行密钥交换协议。密钥交换可以基于匿名的密钥协商协议如 DHKE，一个密码或预共享密钥，一个数字证书等等。有些通讯协议只在开始时交换一次密钥，而有些协议则会随着时间的推移不断地交换密钥。

认证密钥交换（AKE）是一种会同时认证相关方身份的密钥交换协议，比如个人 WiFi 通常就会使用 password-authenticated key agreement (PAKE)，而如果你连接的是公开 WiFi，则会使用匿名密钥交换协议。

目前有许多用于密钥交换的密码算法。其中一些使用公钥密码系统，而另一些则使用更简单的密钥交换方案（如 Diffie-Hellman 密钥交换）；其中有些算法涉及服务器身份验证，也有些涉及客户端身份验证；其中部分算法使用密码，另一部分使用数字证书或其他身份验证机制。下面列举一些知名的密钥交换算法：

Diffie-Hellman Key Exchange (DHКЕ) ：传统的、应用最为广泛的密钥交换协议
椭圆曲线 Diffie-Hellman (ECDH)
RSA-OAEP 和 RSA-KEM（RSA 密钥传输）
PSK（预共享密钥）
SRP（安全远程密码协议）
FHMQV（Fully Hashed Menezes-Qu-Vanstone）
ECMQV（Ellictic-Curve Menezes-Qu-Vanstone）
CECPQ1（量子安全密钥协议）

1、Diffie–Hellman 密钥交换

迪菲-赫尔曼密钥交换（Diffie–Hellman Key Exchange）是一种安全协议，它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道安全地协商出一个安全密钥，而且任何窃听者都无法得知密钥信息。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。

DHKE 可以防范嗅探攻击（窃听），但是无法抵挡中间人攻击（中继）。

DHKE 有两种实现方案：

传统的 DHKE 算法：使用离散对数实现
基于椭圆曲线密码学的 ECDH

为了理解 DHKE 如何实现在「大庭广众之下」安全地协商出密钥，我们首先使用色彩混合来形象地解释下它大致的思路。

跟编程语言的 Hello World 一样，密钥交换的解释通常会使用 Alice 跟 Bob 来作为通信双方。现在他俩想要在公开的信道上，协商出一个秘密色彩出来，但是不希望其他任何人知道这个秘密色彩。他们可以这样做：

分步解释如下：

首先 Alice 跟 Bob 沟通，确定一个初始的色彩，比如黄色。这个沟通不需要保密。
然后，Alice 跟 Bob 分别偷偷地选择出一个自己的秘密色彩，这个就得保密啦。
现在 Alice 跟 Bob，分别将初始色彩跟自己选择的秘密色彩混合，分别得到两个混合色彩。
之后，Alice 跟 Bob 再回到公开信道上，交换双方的混合色彩。
- 我们假设在仅知道初始色彩跟混合色彩的情况下，很难推导出被混合的秘密色彩。这样第三方就猜不出 Bob 跟 Alice 分别选择了什么秘密色彩了。
最后 Alice 跟 Bob 再分别将自己的秘密色彩，跟对方的混合色彩混合，就得到了最终的秘密色彩。这个最终色彩只有 Alice 跟 Bob 知道，信道上的任何人都无法猜出来。

DHKE 协议也是基于类似的原理，但是使用的是离散对数（discrete logarithms）跟模幂（modular exponentiations）而不是色彩混合。

2、经典 DHKE 协议

基础数学知识

3、DHKE 密钥交换流程

下面该轮到 Alice 跟 Bob 出场来介绍 DHKE 的过程了，先看图（下面绿色表示非秘密信息，红色表示秘密信息）：

使用 Python 演示下大概是这样：

# pip install cryptography==36.0.1
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.asymmetric import dh

# 1. 双方协商使用两个独特的正整数 g 与 p
## generator => 即基数 g，通常使用 2, 有时也使用 5
## key_size => 模数 p 的长度，通常使用 2048-3096 位（2048 位的安全性正在减弱）
params = dh.generate_parameters(generator=2, key_size=2048)
param_numbers = params.parameter_numbers()
g = param_numbers.g  # => 肯定是 2
p = param_numbers.p  # => 一个 2048 位的整数
print(f"{g=}, {p=}")

# 2. Alice 生成自己的秘密整数 a 与公开整数 A
alice_priv_key = params.generate_private_key()
a = alice_priv_key.private_numbers().x
A = alice_priv_key.private_numbers().public_numbers.y
print(f"{a=}")
print(f"{A=}")

# 3. Bob 生成自己的秘密整数 b 与公开整数 B
bob_priv_key = params.generate_private_key()
b = bob_priv_key.private_numbers().x
B = bob_priv_key.private_numbers().public_numbers.y
print(f"{b=}")
print(f"{B=}")

# 4. Alice 与 Bob 公开交换整数 A 跟 B（即各自的公钥）

# 5. Alice 使用 a B 与 p 计算出共享密钥
## 首先使用 B p g 构造出 bob 的公钥对象（实际上 g 不参与计算）
bob_pub_numbers = dh.DHPublicNumbers(B, param_numbers)
bob_pub_key = bob_pub_numbers.public_key()
## 计算共享密钥
alice_shared_key = alice_priv_key.exchange(bob_pub_key)

# 6. Bob 使用 b A 与 p 计算出共享密钥
## 首先使用 A p g 构造出 alice 的公钥对象（实际上 g 不参与计算）
alice_pub_numbers = dh.DHPublicNumbers(A, param_numbers)
alice_pub_key = alice_pub_numbers.public_key()
## 计算共享密钥
bob_shared_key = bob_priv_key.exchange(alice_pub_key)

# 两者应该完全相等， Alice 与 Bob 完成第一次密钥交换
alice_shared_key == bob_shared_key

# 7. Alice 与 Bob 使用 shared_key 进行对称加密通讯

4、新一代 ECDH 协议

Elliptic-Curve Diffie-Hellman (ECDH) 是一种匿名密钥协商协议，它允许两方，每方都有一个椭圆曲线公钥-私钥对，它的功能也是让双方在完全没有对方任何预先信息的条件下通过不安全信道安全地协商出一个安全密钥。

ECDH 是经典 DHKE 协议的变体，其中模幂计算被椭圆曲线的乘法计算取代，以提高安全性。

ECDH 跟前面介绍的 DHKE 非常相似，只要你理解了椭圆曲线的数学原理，结合前面已经介绍了的 DHKE，基本上可以秒懂。我会在后面「非对称算法」一文中简单介绍椭圆曲线的数学原理，不过这里也可以先提一下 ECDH 依赖的公式（其中 a,b为常数，G 为椭圆曲线上的某一点的坐标 (x,y)）：

(a∗G)∗b=(b∗G)∗a

这个公式还是挺直观的吧，感觉小学生也能理解个大概。下面简单介绍下 ECDH 的流程：

Alice 跟 Bob 协商好椭圆曲线的各项参数，以及基点 G，这些参数都是公开的。
Alice 生成一个随机的 ECC 密钥对（公钥：alicePrivate∗G, 私钥: alicePrivate）
Bob 生成一个随机的 ECC 密钥对（公钥：bobPrivate∗G, 私钥: bobPrivate）
两人通过不安全的信道交换公钥
Alice 将 Bob 的公钥乘上自己的私钥，得到共享密钥 sharedKey=(bobPrivate∗G)∗alicePrivate
Bob 将 Alice 的公钥乘上自己的私钥，得到共享密钥 sharedKey=(alicePrivate∗G)∗bobPrivate
因为前面提到的公式，Alice 与 Bob 计算出的共享密钥应该是相等的

这样两方就通过 ECDH 完成了密钥交换。

而 ECDH 的安全性，则由 ECDLP 问题提供保证。这个问题是说，「通过公开的 kG以及 G这两个参数，目前没有有效的手段能快速求解出 k的值。」

从上面的流程中能看到，公钥就是 ECDLP 中的 kG，另外 G 也是公开的，而私钥就是 ECDLP 中的 k。因为 ECDLP 问题的存在，攻击者破解不出 Alice 跟 Bob 的私钥。

代码示例：

# pip install tinyec  # ECC 曲线库
from tinyec import registry
import secrets

def compress(pubKey):
    return hex(pubKey.x) + hex(pubKey.y % 2)[2:]

curve = registry.get_curve('brainpoolP256r1')

alicePrivKey = secrets.randbelow(curve.field.n)
alicePubKey = alicePrivKey * curve.g
print("Alice public key:", compress(alicePubKey))

bobPrivKey = secrets.randbelow(curve.field.n)
bobPubKey = bobPrivKey * curve.g
print("Bob public key:", compress(bobPubKey))

print("Now exchange the public keys (e.g. through Internet)")

aliceSharedKey = alicePrivKey * bobPubKey
print("Alice shared key:", compress(aliceSharedKey))

bobSharedKey = bobPrivKey * alicePubKey
print("Bob shared key:", compress(bobSharedKey))

print("Equal shared keys:", aliceSharedKey == bobSharedKey)

5、PFS 完美前向保密协议 DHE/ECDHE

前面介绍的经典 DHKE 与 ECDH 协议流程，都是在最开始时交换一次密钥，之后就一直使用该密钥通讯。因此如果密钥被破解，整个会话的所有信息对攻击者而言就完全透明了。

为了进一步提高安全性，密码学家提出了「完全前向保密（Perfect Forward Secrecy，PFS）」的概念，并在 DHKE 与 ECDH 的基础上提出了支持 PFS 的 DHE/ECDHE 协议（末尾的 E 是 ephemeral 的缩写，即指所有的共享密钥都是临时的）。

完全前向保密是指长期使用的主密钥泄漏不会导致过去的会话密钥泄漏，从而保护过去进行的通讯不受密码或密钥在未来暴露的威胁。

下面使用 Python 演示下 DHE 协议的流程（ECDHE 的流程也完全类似）：

# pip install cryptography==36.0.1
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.asymmetric import dh

# 1. 双方协商使用两个独特的正整数 g 与 p
## generator => 即基数 g，通常使用 2, 有时也使用 5
## key_size => 模数 p 的长度，通常使用 2048-3096 位（2048 位的安全性正在减弱）
params = dh.generate_parameters(generator=2, key_size=2048)
param_numbers = params.parameter_numbers()
g = param_numbers.g  # => 肯定是 2
p = param_numbers.p  # => 一个 2048 位的整数
print(f"{g=}, {p=}")

# 2. Alice 生成自己的秘密整数 a 与公开整数 A
alice_priv_key = params.generate_private_key()
a = alice_priv_key.private_numbers().x
A = alice_priv_key.private_numbers().public_numbers.y
print(f"{a=}")
print(f"{A=}")

# 3. Bob 生成自己的秘密整数 b 与公开整数 B
bob_priv_key = params.generate_private_key()
b = bob_priv_key.private_numbers().x
B = bob_priv_key.private_numbers().public_numbers.y
print(f"{b=}")
print(f"{B=}")

# 4. Alice 与 Bob 公开交换整数 A 跟 B（即各自的公钥）

# 5. Alice 使用 a B 与 p 计算出共享密钥
## 首先使用 B p g 构造出 bob 的公钥对象（实际上 g 不参与计算）
bob_pub_numbers = dh.DHPublicNumbers(B, param_numbers)
bob_pub_key = bob_pub_numbers.public_key()
## 计算共享密钥
alice_shared_key = alice_priv_key.exchange(bob_pub_key)

# 6. Bob 使用 b A 与 p 计算出共享密钥
## 首先使用 A p g 构造出 alice 的公钥对象（实际上 g 不参与计算）
alice_pub_numbers = dh.DHPublicNumbers(A, param_numbers)
alice_pub_key = alice_pub_numbers.public_key()
## 计算共享密钥
bob_shared_key = bob_priv_key.exchange(alice_pub_key)

# 上面的流程跟经典 DHKE 完全一致，代码也是从前面 Copy 下来的
# 但是从这里开始，进入 DHE 协议补充的部分

shared_key_1 = bob_shared_key # 第一个共享密钥

# 7. 假设 Bob 现在要发送消息 M_b_1 给 Alice
## 首先 Bob 使用对称加密算法加密消息 M_b
M_b_1 = "Hello Alice, I'm bob~"
C_b_1 = Encrypt(M_b_1, shared_key_1)  # Encrypt 是某种对称加密方案的加密算法，如 AES-256-CTR-HMAC-SHA-256
## 然后 Bob 需要生成一个新的公私钥 b_2 与 B_2（注意 g 与 p 两个参数是不变的）
bob_priv_key_2 = parameters.generate_private_key()
b_2 = bob_priv_key.private_numbers().x
B_2 = bob_priv_key.private_numbers().public_numbers.y
print(f"{b_2=}")
print(f"{B_2=}")

# 8. Bob 将 C_b_1 与 B_2 一起发送给 Alice

# 9. Alice 首先解密数据 C_b_1 得到原始消息 M_b_1
assert M_b_1 == Decrypt(C_b_1, shared_key_1)  # Dncrypt 是某种对称加密方案的解密算法，如 AES-256-CTR-HMAC-SHA-256
## 然后 Alice 也生成新的公私钥 a_2 与 A_2
alice_priv_key_2 = parameters.generate_private_key()
## Alice 使用 a_2 B_2 与 p 计算出新的共享密钥 shared_key_2
bob_pub_numbers_2 = dh.DHPublicNumbers(B_2, param_numbers)
bob_pub_key_2 = bob_pub_numbers_2.public_key()
shared_key_2 = alice_priv_key_2.exchange(bob_pub_key_2)

# 10. Alice 回复 Bob 消息时，使用新共享密钥 shared_key_2 加密消息得到 C_a_1
# 然后将密文 C_a_1 与 A_2 一起发送给 Bob

# 11. Bob 使用 b_2 A_2 与 p 计算出共享密钥 shared_key_2
# 然后再使用 shared_key_2 解密数据
# Bob 在下次发送消息时，会生成新的 b_3 与 B_3，将 B_3 随密文一起发送

## 依次类推

通过上面的代码描述我们应该能理解到，Alice 与 Bob 每次交换数据，实际上都会生成新的临时共享密钥，公钥密钥在每次数据交换时都会更新。即使攻击者破解了花费了很大的代价破解了其中某一个临时共享密钥 shared_key_k（或者该密钥因为某种原因泄漏了），它也只能解密出其中某一次数据交换的信息 M_b_k，其他所有的消息仍然是保密的，不受此次攻击（或泄漏）的影响。

六、对称密钥加密算法

两个常用动词：

加密：cipher 或者 encrypt
解密：decipher 或者 decrypt

另外有几个名词有必要解释：

cipher: 指用于加解密的「密码算法」，有时也被直接翻译成「密码」
cryptographic algorithm: 密码学算法，泛指密码学相关的各类算法
ciphertext: 密文，即加密后的信息。对应的词是明文 plaintext
password: 这个应该不需要解释，就是我们日常用的各种字符或者数字密码，也可称作口令。
passphrase: 翻译成「密码词组」或者「密碼片語」，通常指用于保护密钥或者其他敏感数据的一个 password
- 如果你用 ssh/gpg/openssl 等工具生成或使用过密钥，应该对它不陌生。

在密码学里面，最容易搞混的词估计就是「密码」了，cipher/password/passphrase 都可以被翻译成「密码」，需要注意下其中区别。

1、什么是对称加密

在密码学中，有两种加密方案被广泛使用：「对称加密」与「非对称加密」。

对称加密是指，使用相同的密钥进行消息的加密与解密。因为这个特性，我们也称这个密钥为「共享密钥（Shared Secret Key）」，示意图如下：

现代密码学中广泛使用的对称加密算法（ciphers）有：AES（AES-128、AES-192、AES-256）、ChaCha20、Twofish、IDEA、Serpent、Camelia、RC6、CAST 等。其中绝大多数都是「块密码算法（Block Cipher）」或者叫「分组密码算法」，这种算法一次只能加密固定大小的块（例如 128 位）；少部分是「流密码算法（Stream Cipher）」，流密码算法将数据逐字节地加密为密文流。

通过使用称为「分组密码工作模式」的技术，可以将「分组密码算法」转换为「流密码算法」。

量子安全性

即使计算机进入量子时代，仍然可以沿用当前的对称密码算法。因为大多数现代对称密钥密码算法都是抗量子的（quantum-resistant），这意味当使用长度足够的密钥时，强大的量子计算机无法破坏其安全性。目前来看 256 位的 AES/Twofish 在很长一段时间内都将是 量子安全 的。

2、对称加密方案的结构

我们在第一章「概览」里介绍过，单纯使用数据加密算法只能保证数据的安全性，并不能满足我们对消息真实性、完整性与不可否认性的需求，因此通常我们会将对称加密算法跟其他算法组合成一个「对称加密方案」来使用，这种多个密码学算法组成的「加密方案」能同时保证数据的安全性、真实性、完整性与不可否认性。

一个分组加密方案通常会包含如下几种算法：

将密码转换为密钥的密钥派生算法 KDF（如 Scrypt 或 Argon2）：通过使用 KDF，加密方案可以允许用户使用字符密码作为「Shared Secret Key」，并使密码的破解变得困难和缓慢
分组密码工作模式（用于将分组密码转换为流密码，如 CBC 或 CTR）+ 消息填充算法（如 PKCS7）：分组密码算法（如 AES）需要借助这两种算法，才能加密任意大小的数据
分组密码算法（如 AES）：使用密钥安全地加密固定长度的数据块
- 大多数流行的对称加密算法，都是分组密码算法
消息认证算法（如HMAC）：用于验证消息的真实性、完整性、不可否认性

而一个流密码加密方案本身就能加密任意长度的数据，因此不需要「分组密码模式」与「消息填充算法」。

如 AES-256-CTR-HMAC-SHA256 就表示一个使用 AES-256 与 Counter 分组模式进行加密，使用 HMAC-SHA256 进行消息认证的加密方案。其他流行的对称加密方案还有 ChaCha20-Poly1305 和 AES-128-GCM 等，其中 ChaCha20-Poly130 是一个流密码加密方案。我们会在后面单独介绍这两种加密方案。

3、分组密码工作模式

「分组密码工作模式」可以将「分组密码算法」转换为「流密码算法」，从而实现加密任意长度的数据，这里主要就具体介绍下这个分组密码工作模式（下文简称为「分组模式」或者「XXX 模式」）。

加密方案的名称中就带有具体的「分组模式」名称，如：

AES-256-GCM - 具有 256 位加密密钥和 GCM 分组模式的 AES 密码
AES-128-CTR - 具有 128 位加密密钥和 CTR 分组模式的 AES 密码
Serpent-128-CBC - 具有 128 位加密密钥和 CBC 分组模式的 Serpent 密码

「分组密码工作模式」背后的主要思想是把明文分成多个长度固定的组，再在这些分组上重复应用分组密码算法进行加密/解密，以实现安全地加密/解密任意长度的数据。

某些分组模式（如 CBC）要求将输入拆分为分组，并使用填充算法（例如添加特殊填充字符）将最末尾的分组填充到块大小。也有些分组模式（如 CTR、CFB、OFB、CCM、EAX 和 GCM）根本不需要填充，因为它们在每个步骤中，都直接在明文部分和内部密码状态之间执行异或（XOR）运算.

使用「分组模式」加密大量数据的流程基本如下：

初始化加密算法状态（使用加密密钥 + 初始向量 IV）
加密数据的第一个分组
使用加密密钥和其他参数转换加密算法的当前状态
加密下一个分组
再次转换加密状态
再加密下一分组
依此类推，直到处理完所有输入数据

解密的流程跟加密完全类似：先初始化算法，然后依次解密所有分组，中间可能会涉及到加密状态的转换。

下面我们来具体介绍下 CTR 与 GCM 两个常见的分组模式。

0. 初始向量 IV

介绍具体的分组模式前，需要先了解下初始向量 IV（Initialization Vector）这个概念，它有时也被称作 Salt 或者 Nonce。初始向量 IV 通常是一个随机数，主要作用是往密文中添加随机性，使同样的明文被多次加密也会产生不同的密文，从而确保密文的不可预测性。

IV 的大小应与密码块大小相同，例如 AES、Serpent 和 Camellia 都只支持 128 位密码块，那么它们需要的 IV 也必须也 128 位。

IV 通常无需保密，但是应当足够随机（无法预测），而且不允许重用，应该对每条加密消息使用随机且不可预测的 IV。

一个常见错误是使用相同的对称密钥和相同的 IV 加密多条消息，这使得针对大多数分组模式的各种加密攻击成为可能。

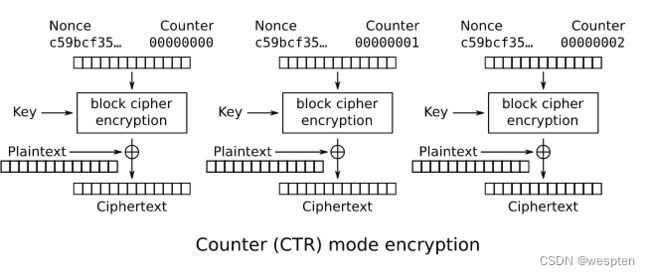
1. CTR (Counter) 分组模式

参考文档: SP 800-38A, Block Cipher Modes of Operation: Methods and Techniques | CSRC

下图说明了「CTR 分组工作模式」的加密解密流程，基本上就是将明文/密文拆分成一个个长度固定的分组，然后使用一定的算法进行加密与解密：

可以看到两图中左边的第一个步骤，涉及到三个参数：

Nonce，初始向量 IV 的别名，前面已经介绍过了。
Counter: 一个计数器，最常用的 Counter 实现是「从 0 开始，每次计算都自增 1」
Key: 对称加密的密钥
Plaintext: 明文的一个分组。除了最后一个分组外，其他分组的长度应该跟 Key 相同

CTR 模式加解密的算法使用公式来表示如下：

公式的符号说明如下：

Python 中最流行的密码学库是 cryptography，requests 的底层曾经就使用了它（新版本已经换成使用标准库 ssl 了），下面我们使用这个库来演示下 AES-256-CTR 算法：

# pip install cryptography==36.0.1
import os
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes

plaintext = b"this is a test message, hahahahahaha~"

# 使用 32bytes 的 key，即使用算法 AES-256-CTR
key = os.urandom(32)
# key => b'\x96\xec.\xc7\xd5\x1b/5\xa1\x10s\x9d\xd5\x10z\xdc\x90\xb5\x1cm">x\xfd \xd5\xc5\xaf\x19\xd1Z\xbb'

# AES 算法的 block 大小是固定的 128bits，即 16 bytes, IV 长度需要与 block 一致
iv = os.urandom(16)
# iv => b'\x88[\xc9\n`\xe4\xc2^\xaf\xdc\x1e\xfd.c>='

# 1. 发送方加密数据
## 构建 AES-256-CTR 的 cipher，然后加密数据，得到密文
cipher = Cipher(algorithms.AES(key), modes.CTR(iv))
encryptor = cipher.encryptor()
ciphertext = encryptor.update(plaintext) + encryptor.finalize()
# ciphertext => b'\x9b6(\x1d\xfd\xde\x96S\x8b\x8f\x90\xc5}ou\x9e\xb1\xbd\x9af\xb8\xdc\xec\xbf\xa3"\x18^\xac\x14\xc8s2*\x1a\xcf\x1d'

# 2. 发送方将 iv + ciphertext 发送给接收方

# 3. 接收方解密数据
# 接收方使用自己的 key + 接收到的 iv，构建 cipher，然后解密出原始数据
cipher = Cipher(algorithms.AES(key), modes.CTR(iv))
decryptor = cipher.decryptor()
decryptor.update(ciphertext) + decryptor.finalize()

从上面的算法描述能感觉到，CTR 算法还蛮简单的。下面我使用 Python 写一个能够 work 的 CTR 实现：


def xor_bytes(a, b):
    """Returns a new byte array with the elements xor'ed.
       if len(a) != len(b), extra parts are discard.
    """
    return bytes(i^j for i, j in zip(a, b))

def inc_bytes(a):
    """ Returns a new byte array with the value increment by 1 """
    out = list(a)
    for i in reversed(range(len(out))):
        if out[i] == 0xFF:
            out[i] = 0
        else:
            out[i] += 1
            break
    return bytes(out)

def split_blocks(message, block_size, require_padding=True):
    """
    Split `message` with fixed length `block_size`
    """
    assert len(message) % block_size == 0 or not require_padding
    return [message[i:i+16] for i in range(0, len(message), block_size)]

def encrypt_ctr(block_cipher, plaintext, iv):
    """
    Encrypts `plaintext` using CTR mode with the given nounce/IV.
    """
    assert len(iv) == 16

    blocks = []
    nonce = iv
    for plaintext_block in split_blocks(plaintext, block_size=16, require_padding=False):
        # CTR mode encrypt: plaintext_block XOR encrypt(nonce)
        o = bytes(block_cipher.encrypt(nonce))
        block = xor_bytes(plaintext_block, o)  # extra parts of `o` are discard in this step
        blocks.append(block)
        nonce = inc_bytes(nonce)

    return b''.join(blocks)

# 加密与解密的算法完全一致
decrypt_ctr = encrypt_ctr

接下来验证下算法的正确性：

# Python 官方库未提供 AES 实现，因此需要先装下这个库：
# pip install pyaes==1.6.1
from pyaes import AES

# AES-256-CTR - plaintext key 都与前面的测试代码完全一致
plaintext = b"this is a test message, hahahahahaha~"
key = b'\x96\xec.\xc7\xd5\x1b/5\xa1\x10s\x9d\xd5\x10z\xdc\x90\xb5\x1cm">x\xfd \xd5\xc5\xaf\x19\xd1Z\xbb'

# 1. 发送方加密数据
# 首先生成一个随机 IV，为了对比，这里使用前面生成好的数据
iv = b'\x88[\xc9\n`\xe4\xc2^\xaf\xdc\x1e\xfd.c>='
aes_cipher = AES(key)
ciphertext = encrypt_ctr(aes_cipher, plaintext, iv)
print("ciphertext =>", bytes(ciphertext)) # 输出应该与前面用 cryptography 计算出来的完全一致
# ciphertext => b'\x9b6(\x1d\xfd\xde\x96S\x8b\x8f\x90\xc5}ou\x9e\xb1\xbd\x9af\xb8\xdc\xec\xbf\xa3"\x18^\xac\x14\xc8s2*\x1a\xcf\x1d'

# 2. 发送方将 ciphertext + iv 发送给接收方

# 3. 接收方使用自己的 key 解密数据
aes_cipher = AES(key)
decrypted_bytes = decrypt_ctr(aes_cipher, ciphertext, iv)
print("decrypted_bytes =>", bytes(decrypted_bytes))
# decrypted_bytes => b"this is a test message, hahahahahaha~"

2. GCM (Galois/Counter) 分组模式

GCM (Galois/Counter) 模式在 CTR 模式的基础上，添加了消息认证的功能，而且同时还具有与 CTR 模式相同的并行计算能力。因此相比 CTR 模式，GCM 不仅速度一样快，还能额外提供对消息完整性、真实性的验证能力。

下图直观地解释了 GCM 块模式（Galois/Counter 模式）的工作原理：

GCM 模式新增的 Auth Tag，计算起来会有些复杂，我们就直接略过了，对原理感兴趣的可以看下 Galois/Counter_Mode_wiki.

3. 如何选用块模式

一些 Tips:

常用的安全块模式是 CBC（密码块链接）、CTR（计数器）和 GCM（伽罗瓦/计数器模式），它们需要一个随机（不可预测的）初始化向量 (IV)，也称为 nonce 或 salt
「CTR（Counter）」块模式在大多数情况下是一个不错的选择，因为它具有很强的安全性和并行处理能力，允许任意输入数据长度（无填充）。但它不提供身份验证和完整性，只提供加密
GCM（Galois/Counter Mode）块模式继承了 CTR 模式的所有优点，并增加了加密消息认证能力。GCM 是在对称密码中实现认证加密的快速有效的方法，强烈推荐
CBC 模式在固定大小的分组上工作。因此，在将输入数据拆分为分组后，应使用填充算法使最后一个分组的长度一致。大多数应用程序使用 PKCS7 填充方案或 ANSI X.923. 在某些情况下，CBC 阻塞模式可能容易受到「padding oracle」攻击，因此最好避免使用 CBC 模式
众所周知的不安全块模式是 ECB（电子密码本），它将相等的输入块加密为相等的输出块（无加密扩散能力）。不要使用 ECB 块模式！它可能会危及整个加密方案。
CBC、CTR 和 GCM 模式等大多数块都支持「随机访问」解密。比如在视频播放器中的任意时间偏移处寻找，播放加密的视频流

总之，建议使用 CTR (Counter) 或 GCM (Galois/Counter) 分组模式。其他的分组在某些情况下可能会有所帮助，但很可能有安全隐患，因此除非你很清楚自己在做什么，否则不要使用其他分组模式！

CTR 和 GCM 加密模式有很多优点：它们是安全的（目前没有已知的重大缺陷），可以加密任意长度的数据而无需填充，可以并行加密和解密分组（在多核 CPU 中）并可以直接解密任意一个密文分组。因此它们适用于加密加密钱包、文档和流视频（用户可以按时间查找）。 GCM 还提供消息认证，是一般情况下密码块模式的推荐选择。

请注意，GCM、CTR 和其他分组模式会泄漏原始消息的长度，因为它们生成的密文长度与明文消息的长度相同。如果您想避免泄露原始明文长度，可以在加密前向明文添加一些随机字节（额外的填充数据），并在解密后将其删除。

4、对称加密算法与对称加密方案

前面啰嗦了这么多，下面进入正题：对称加密算法

安全的对称加密算法

目前应用最广泛的对称加密算法，是 AES 跟 Salsa20 / ChaCha20 这两个系列。

1. AES (Rijndael)

AES（高级加密标准，也称为 Rijndael）是现代 IT 行业中最流行和广泛使用的对称加密算法。AES 被证明是高度安全、快速且标准化的，到目前为止没有发现任何明显的弱点或攻击手段，而且几乎在所有平台上都得到了很好的支持。 AES 是 128 位分组密码，使用 128、192 或 256 位密钥。它通常与分组模式组合成分组加密方案（如 AES-CTR 或 AES-GCM）以处理流数据。在大多数分组模式中，AES 还需要一个随机的 128 位初始向量 IV。

Rijndael (AES) 算法可免费用于任何用途，而且非常流行。很多站点都选择 AES 作为 TLS 协议的一部分，以实现安全通信。现代 CPU 硬件基本都在微处理器级别实现了 AES 指令以加速 AES 加密解密操作。

这里有一个纯 Python 的 AES 实现可供参考: AES encryption in pure Python - boppreh

我们在前面的 CTR 分组模式中已经使用 Python 实践了 AES-256-CTR 加密方案。而实际上更常用的是支持集成身份验证加密（AEAD）的 AES-256-GCM 加密方案，它的优势我们前面已经介绍过了，这里我们使用 Python 演示下如何使用：

# pip install cryptography==36.0.1
import os
from cryptography.hazmat.primitives.ciphers import (
    Cipher, algorithms, modes
)

def encrypt(key, plaintext, associated_data):
    # Generate a random 96-bit IV.
    iv = os.urandom(12)

    # Construct an AES-GCM Cipher object with the given key and a
    # randomly generated IV.
    encryptor = Cipher(
        algorithms.AES(key),
        modes.GCM(iv),
    ).encryptor()

    # associated_data will be authenticated but not encrypted,
    # it must also be passed in on decryption.
    encryptor.authenticate_additional_data(associated_data)

    # Encrypt the plaintext and get the associated ciphertext.
    # GCM does not require padding.
    ciphertext = encryptor.update(plaintext) + encryptor.finalize()

    return (iv, ciphertext, encryptor.tag)

def decrypt(key, associated_data, iv, ciphertext, tag):
    # Construct a Cipher object, with the key, iv, and additionally the
    # GCM tag used for authenticating the message.
    decryptor = Cipher(
        algorithms.AES(key),
        modes.GCM(iv, tag),
    ).decryptor()

    # We put associated_data back in or the tag will fail to verify
    # when we finalize the decryptor.
    decryptor.authenticate_additional_data(associated_data)

    # Decryption gets us the authenticated plaintext.
    # If the tag does not match an InvalidTag exception will be raised.
    return decryptor.update(ciphertext) + decryptor.finalize()


# 接下来进行算法验证

plaintext = b"this is a paintext, hahahahahaha~"
key = b'\x96\xec.\xc7\xd5\x1b/5\xa1\x10s\x9d\xd5\x10z\xdc\x90\xb5\x1cm">x\xfd \xd5\xc5\xaf\x19\xd1Z\xbb'
associated_data = b"authenticated but not encrypted payload"  # 被用于消息认证的关联数据

# 1. 发送方加密消息
iv, ciphertext, tag = encrypt(
    key,
    plaintext,
    associated_data
)

# 2. 发送方将 associated_data iv ciphertext tag 打包发送给接收方

# 3. 接收方使用自己的 key 验证并解密数据
descrypt_text = decrypt(
    key,
    associated_data,
    iv,
    ciphertext,
    tag
)

2. Salsa20 / ChaCha20

Salsa20 及其改进的变体 ChaCha（ChaCha8、ChaCha12、ChaCha20）和 XSalsa20 是由密码学家 Daniel Bernstein 设计的现代、快速的对称流密码家族。 Salsa20 密码是对称流密码设计竞赛 eSTREAM（2004-2008）的决赛选手之一，它随后与相关的 BLAKE 哈希函数一起被广泛采用。 Salsa20 及其变体是免版税的，没有专利。

Salsa20 密码将 128 位或 256 位对称密钥 + 随机生成的 64 位随机数（初始向量）和无限长度的数据流作为输入，并生成长度相同的加密数据流作为输出输入流。

3. ChaCha20-Poly1305

Salsa20 应用最为广泛的是认证加密方案：ChaCha20-Poly1305，即组合使用 ChaCha20 与消息认证算法 Poly1305，它们都由密码学家 Bernstein 设计。

ChaCha20-Poly1305 已被证明足够安全，不过跟 GCM 一样它的安全性也依赖于足够随机的初始向量 IV，另外 ChaCha20-Poly1305 也不容易遭受计时攻击。

在没有硬件加速的情况下，ChaCha20 通常比 AES 要快得多（比如在旧的没有硬件加速的移动设备上），这是它最大的优势。

以下是一个 ChaCha20 的 Python 示例：

# pip install cryptography==36.0.1
import os
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes

plaintext = b"this is a paintext, hahahahahaha~"
key = b'\x96\xec.\xc7\xd5\x1b/5\xa1\x10s\x9d\xd5\x10z\xdc\x90\xb5\x1cm">x\xfd \xd5\xc5\xaf\x19\xd1Z\xbb'
nonce = os.urandom(16)

algorithm = algorithms.ChaCha20(key, nonce)
# ChaCha20 是一个流密码，mode 必须为 None
cipher = Cipher(algorithm, mode=None)

# 1. 加密
encryptor = cipher.encryptor()
ct = encryptor.update(plaintext)

# 2. 解密
decryptor = cipher.decryptor()
decryptor.update(ct)

4. 其他流行的对称加密算法

还有一些其他的现代安全对称密码，它们的应用不如 AES 和 ChaCha20 这么广泛，但在程序员和信息安全社区中仍然很流行：

Serpent - 安全对称密钥分组密码（密钥大小：128、192 或 256 位），公众所有（Public Domain），完全免费
Twofish - 安全对称密钥分组密码（密钥大小：128、192 或 256 位），公众所有（Public Domain），完全免费
Camellia - 安全对称密钥分组密码（分组大小：128 位；密钥大小：128、192 和 256 位），专利算法，但完全免费
- 该算法由三菱和日本电信电话（NTT）在 2000 年共同发明
RC5 - 安全对称密钥分组密码（密钥大小：128 到 2040 位；分组大小：32、64 或 128 位；轮数：1 … 255），短密钥不安全（56 位密钥已被暴力破解） , 专利在 2015 年到期，现在完全免费
RC6 - 安全对称密钥分组密码，类似于 RC5，但更复杂（密钥大小：128 到 2040 位；分组大小：32、64 或 128 位；轮数：1 … 255），专利在 2017 年到期，现在完全免费
IDEA - 安全对称密钥分组密码（密钥大小：128 位），所有专利在均 2012 年前过期，完全免费
CAST (CAST-128 / CAST5, CAST-256 / CAST6) - 安全对称密钥分组密码系列（密钥大小：40 … 256 位），免版税
ARIA - 安全对称密钥分组密码，类似于 AES（密钥大小：128、192 或 256 位），韩国官方标准，免费供公众使用
SM4 - 安全对称密钥分组密码，类似于 AES（密钥大小：128 位），中国官方标准，免费供公众使用
- 由中国国家密码管理局于 2012 年 3 月 21 日发布

具体的算法内容这里就不介绍了，有兴趣或者用得到的时候，可以再去仔细了解。

不安全的对称加密算法

如下这些对称加密算法曾经很流行，但现在被认为是不安全的或有争议的安全性，不建议再使用：

DES - 56 位密钥大小，可以被暴力破解
3DES（三重 DES, TDES）- 64 位密码，被认为不安全，已在 2017 年被 NIST 弃用.
RC2 - 64 位密码，被认为不安全
RC4 - 流密码，已被破解，网上存在大量它的破解资料
Blowfish - 旧的 64 位密码，已被破坏
- Sweet32: Birthday attacks on 64-bit block ciphers in TLS and OpenVPN
GOST - 俄罗斯 64 位分组密码，有争议的安全性，被认为有风险

对称认证加密算法 AE / AEAD

前面「MAC 与密钥派生函数 KDF」中介绍过 AE 认证加密及其变体 AEAD.

一些对称加密方案提供集成身份验证加密（AEAD），比如使用了 GCM 分组模式的加密方案 AES-GCM，而其他加密方案（如 AES-CBC 和 AES-CTR）自身不提供身份验证能力，需要额外添加。

最流行的认证加密（AEAD）方案有如下几个，我们在之前已经简单介绍过它们：

ChaCha20-Poly1305
- 具有集成 Poly1305 身份验证器的 ChaCha20 流密码（集成身份验证 AEAD 加密）
- 使用 256 位密钥和 96 位随机数（初始向量）
- 极高的性能
- 在硬件不支持 AES 加速指令时（如路由器、旧手机等硬件上），推荐使用此算法
AES-256-GCM
- 我们在前面的 GCM 模式一节，使用 Python 实现并验证了这个 AES-256-GCM 加密方案
- 使用 256 位密钥和 128 位随机数（初始向量）
- 较高的性能
- 在硬件支持 AES 加速时（如桌面、服务器等场景），更推荐使用此算法
AES-128-GCM
- 跟 AES-256-GCM 一样，区别在于它使用 128 位密钥，安全性弱于 ChaCha20-Poly1305 与 AES-256-GCM.
- 目前被广泛应用在 HTTPS 等多种加密场景下，但是正在慢慢被前面两种方案取代

今天的大多数应用程序应该优先选用上面这些加密方案进行对称加密，而不是自己造轮子。上述方案是高度安全的、经过验证的、经过良好测试的，并且大多数加密库都已经提供了高效的实现，可以说是开箱即用。

目前应用最广泛的对称加密方案应该是 AES-128-GCM，而 ChaCha20-Poly1305 因为其极高的性能，也越来越多地被应用在 TLS1.2、TLS1.3、QUIC/HTTP3、Wireguard、SSH 等协议中。

5、AES 算法案例：以太坊钱包加密

在这一小节我们研究一个现实中的 AES 应用场景：以太坊区块链的标准加密钱包文件格式。我们将看到 AES-128-CTR 密码方案如何与 Scrypt 和 MAC 相结合，通过字符密码安全地实现经过身份验证的对称密钥加密。

以太坊 UTC / JSON 钱包

在比特币和以太坊等区块链网络中，区块链资产持有者的私钥存储在称为加密钱包的特殊密钥库中。通常，这些加密钱包是本地硬盘上的文件，并使用字符密码加密。

在以太坊区块链中，加密钱包以一种特殊的加密格式在内部存储，称为「UTC / JSON 钱包（密钥库文件）」或「Web3 秘密存储定义」。这是一种加密钱包的文件格式，被广泛应用在 geth 和 Parity（以太坊的主要协议实现）、MyEtherWallet（流行的在线客户端以太坊钱包）、MetaMask（广泛使用的浏览器内以太坊钱包）、ethers.js 和 Nethereum 库以及许多其他与以太坊相关的技术和工具中。

以太坊 UTC/JSON 密钥库将加密的私钥、加密数据、加密算法及其参数保存为 JSON 文本文档。

UTC / JSON 钱包的一个示例如下：

{
  "version": 3,
  "id": "07a9f767-93c5-4842-9afd-b3b083659f04",
  "address": "aef8cad64d29fcc4ed07629b9e896ebc3160a8d0",
  "Crypto": {
    "ciphertext": "99d0e66c67941a08690e48222a58843ef2481e110969325db7ff5284cd3d3093",
    "cipherparams": { "iv": "7d7fabf8dee2e77f0d7e3ff3b965fc23" },
    "cipher": "aes-128-ctr",
    "kdf": "scrypt",
    "kdfparams": {
      "dklen": 32,
      "salt": "85ad073989d461c72358ccaea3551f7ecb8e672503cb05c2ee80cfb6b922f4d4",
      "n": 8192,
      "r": 8,
      "p": 1
      },
    "mac": "06dcf1cc4bffe1616fafe94a2a7087fd79df444756bb17c93af588c3ab02a913"
  }
}

上述 json 内容也是认证对称加密的一个典型示例，可以很容易分析出它的一些组成成分：

kdf: 用于从字符密码派生出密钥的 KDF 算法名称，这里用的是 scrypt
- kdfparams: KDF 算法的参数，如迭代参数、盐等…
ciphertext: 钱包内容的密文，通常这就是一个被加密的 256 位私钥
cipher + cipherparams: 对称加密算法的名称及参数，这里使用了 AES-128-CTR，并给出了初始向量 IV
mac: 由 MAC 算法生成的消息认证码，被用于验证解密密码的正确性
- 以太坊使用截取派生密钥的一部分，拼接上完整密文，然后进行 keccak-256 哈希运算得到 MAC 值
其他钱包相关的信息

默认情况下，密钥派生函数是 scrypt 并使用的是弱 scrypt 参数（n=8192 成本因子，r=8 块大小，p=1 并行化），因此建议使用长而复杂的密码以避免钱包被暴力解密。

七、非对称密钥加密算法 RSA/ECC

1、公钥密码学 / 非对称密码学

在介绍非对称密钥加密方案和算法之前，我们首先要了解公钥密码学的概念。

密码学的历史

从第一次世界大战、第二次世界大战到 1976 年这段时期密码的发展阶段，被称为「近代密码阶段」。在近代密码阶段，所有的密码系统都使用对称密码算法——使用相同的密钥进行加解密。当时使用的密码算法在拥有海量计算资源的现代人看来都是非常简单的，我们经常看到各种讲述一二战的谍战片，基本都包含破译电报的片段。

第一二次世界大战期间，无线电被广泛应用于军事通讯，围绕无线电通讯的加密破解攻防战极大地影响了战局。

公元20世纪初，第一次世界大战进行到关键时刻，英国破译密码的专门机构「40号房间」利用缴获的德国密码本破译了著名的「齐默尔曼电报」，其内容显示德国打算联合墨西哥对抗可能会参战的美国，这促使美国放弃中立对德宣战，从而彻底改变了一战的走势。

1943 年，美国从破译的日本电报中得知山本五十六将于 4 月 18 日乘中型轰炸机，由 6 架战斗机护航，到中途岛视察。美国总统罗斯福亲自做出决定截击山本，山本乘坐的飞机在去往中途岛的路上被美军击毁，战争天才山本五十六机毁人亡，日本海军从此一蹶不振。

此外，在二次世界大战中，美军将印第安纳瓦霍土著语言作为密码使用，并特别征募使用印第安纳瓦霍通信兵。在二次世界大战日美的太平洋战场上，美国海军军部让北墨西哥和亚历桑那印第安纳瓦霍族人使用纳瓦霍语进行情报传递。纳瓦霍语的语法、音调及词汇都极为独特，不为世人所知道，当时纳瓦霍族以外的美国人中，能听懂这种语言的也就一二十人。这是密码学和语言学的成功结合，纳瓦霍语密码成为历史上从未被破译的密码。

在 1976 年 Malcolm J. Williamson 公开发表了现在被称为「Diffie–Hellman 密钥交换，DHKE」的算法，并提出了「公钥密码学」的概念，这是密码学领域一项划时代的发明，它宣告了「近代密码阶段」的终结，是「现代密码学」的起点。

言归正传，对称密码算法的问题有两点：

「需要安全的通道进行密钥交换」，早期最常见的是面对面交换密钥
每个点对点通信都需要使用不同的密钥，密钥的管理会变得很困难
- 如果你需要跟 100 个朋友安全通信，你就要维护 100 个不同的对称密钥，而且还得确保它们不泄漏。

这会导致巨大的「密钥交换」跟「密钥保存与管理」的成本。「公钥密码学」最大的优势就是，它解决了这两个问题：

「公钥密码学」可以在不安全的信道上安全地进行密钥交换，第三方即使监听到通信过程，但是（几乎）无法破解出密钥。
每个人只需要公开自己的公钥，就可以跟其他任何人安全地通信。
- 如果你需要跟 100 个朋友安全通信，你们只需要公开自己的公钥。发送消息时使用对方的公钥加密，接收消息时使用自己的私钥解密即可。
- 只有你自己的私钥需要保密，所有的公钥都可以公开，这就显著降低了密钥的维护成本。

因此公钥密码学成为了现代密码学的基石，而「公钥密码学」的诞生时间 1976 年被认为是现代密码学的开端。

公钥密码学的概念

公钥密码系统的密钥始终以公钥 + 私钥对的形式出现，公钥密码系统提供数学框架和算法来生成公钥+私钥对。公钥通常与所有人共享，而私钥则保密。公钥密码系统在设计时就确保了在预期的算力下，几乎不可能从其公开的公钥逆向演算出对应的私钥。

公钥密码系统主要有三大用途：加密与解密、签名与验证、密钥交换。每种算法都需要使用到公钥和私钥，比如由公钥加密的消息只能由私钥解密，由私钥签名的消息需要用公钥验证。

由于加密解密、签名验证均需要两个不同的密钥，故「公钥密码学」也被称为「非对称密码学」。

比较著名的公钥密码系统有：RSA、ECC（椭圆曲线密码学）、ElGamal、Diffie-Hellman、ECDH、ECDSA 和 EdDSA。许多密码算法都是以这些密码系统为基础实现的，例如 RSA 签名、RSA 加密/解密、ECDH 密钥交换以及 ECDSA 和 EdDSA 签名。

量子安全性

目前流行的公钥密码系统基本都依赖于 IFP（整数分解问题）、DLP（离散对数问题）或者 ECDLP（椭圆曲线离散对数问题），这导致这些算法都是量子不安全（quantum-unsafe）的。

如果人类进入量子时代，IFP / DLP / ECDLP 的难度将大大降低，目前流行的 RSA、ECC、ElGamal、Diffie-Hellman、ECDH、ECDSA 和 EdDSA 等公钥密码算法都将被淘汰。

目前已经有一些量子安全的公钥密码系统问世，但是因为它们需要更长的密钥、更长的签名等原因，目前还未被广泛使用。

一些量子安全的公钥密码算法举例：NewHope、NTRU、GLYPH、BLISS、XMSS、Picnic 等，有兴趣的可以自行搜索相关文档。

2、非对称加密方案简介

非对称加密要比对称加密复杂，有如下几个原因：

使用密钥对进行加解密，导致其算法更为复杂
只能加密/解密很短的消息
- 在 RSA 系统中，输入消息应该被转换为大整数（例如使用 OAEP 填充），然后才能进行加密。
一些非对称密码系统（如 ECC）不直接提供加密能力，需要结合使用更复杂的方案才能实现加解密

此外，非对称密码比对称密码慢非常多。比如 RSA 加密比 AES 慢 1000 倍，跟 ChaCha20 就更没法比了。

为了解决上面提到的这些困难并支持加密任意长度的消息，现代密码学使用「非对称加密方案」来实现消息加解密。又因为「对称加密方案」具有速度快、支持加密任意长度消息等特性，「非对称加密方案」通常直接直接组合使用对称加密算法与非对称加密算法。比如「密钥封装机制 KEM（key encapsulation mechanisms)）」与「集成加密方案 IES（Integrated Encryption Scheme）」

1. 密钥封装机制 KEM

顾名思义，KEM 就是仅使用非对称加密算法加密另一个密钥，实际数据的加解密由该密钥完成。

密钥封装机制 KEM 的加密流程（使用公钥加密传输对称密钥）：

密钥封装机制 KEM 的解密流程（使用私钥解密出对称密钥，然后再使用这个对称密钥解密数据）：

RSA-OAEP, RSA-KEM, ECIES-KEM 和 PSEC-KEM. 都是 KEM 加密方案。

密钥封装（Key encapsulation）与密钥包裹（Key wrapping）

主要区别在于使用的是对称加密算法、还是非对称加密算法：

密钥封装（Key encapsulation）指使用非对称密码算法的公钥加密另一个密钥。
密钥包裹（Key wrapping）指使用对称密码算法加密另一个密钥。

2. 集成加密方案 IES

集成加密方案 (IES) 在密钥封装机制（KEM）的基础上，添加了密钥派生算法 KDF、消息认证算法 MAC 等其他密码学算法以达成更高的安全性。

在 IES 方案中，非对称算法（如 RSA 或 ECC）跟 KEM 一样，都是用于加密或封装对称密钥，然后通过对称密钥（如 AES 或 Chacha20）来加密输入消息。

DLIES（离散对数集成加密方案）和 ECIES（椭圆曲线集成加密方案）都是 IES 方案。

3、RSA 密码系统

RSA 密码系统是最早的公钥密码系统之一，它基于 RSA 问题和整数分解问题（IFP）的计算难度。 RSA 算法以其作者（Rivest–Shamir–Adleman）的首字母命名。

RSA 算法在计算机密码学的早期被广泛使用，至今仍然是数字世界应用最广泛的密码算法。但是随着 ECC 密码学的发展，ECC 正在非对称密码系统中慢慢占据主导地位，因为它比 RSA 具有更高的安全性和更短的密钥长度。

RSA 算法提供如下几种功能：

密钥对生成：生成随机私钥（通常大小为 1024-4096 位）和相应的公钥。
加密解密：使用公钥加密消息（消息要先转换为 [0…key_length] 范围内的整数），然后使用密钥解密。
数字签名：签署消息（使用私钥）和验证消息签名（使用公钥）。
- 数字签名实际上是通过 Hash 算法 + 加密解密功能实现的。后面会介绍到，它与一般加解密流程的区别，在于数字签名使用私钥加密，再使用公钥解密。
密钥交换：安全地传输密钥，用于以后的加密通信。

RSA 可以使用不同长度的密钥：1024、2048、3072、4096、8129、16384 甚至更多位。目前 3072 位及以上的密钥长度被认为是安全的，曾经大量使用的 2048 位 RSA 现在被破解的风险在不断提升，已经不推荐使用了。

更长的密钥提供更高的安全性，但会消耗更多的计算时间，同时签名也会变得更长，因此需要在安全性和速度之间进行权衡。非常长的 RSA 密钥（例如 50000 位或 65536 位）对于实际使用可能太慢，例如密钥生成可能需要几分钟到几个小时。

RSA 密钥对生成

RSA 密钥对的生成跟我们在本系列文章的第 5 篇介绍的「DHKE 密钥交换算法」会有些类似，但是要更复杂一点。

首先看下我们怎么使用 openssl 生成一个 1024 位的 RSA 密钥对（仅用做演示，实际应用中建议 3072 位）：

OpenSSL 是目前使用最广泛的网络加密算法库，支持非常多流行的现代密码学算法，几乎所有操作系统都会内置 openssl。

# 生成 1024 位的 RSA 私钥
❯ openssl genrsa -out rsa-private-key.pem 1024
Generating RSA private key, 1024 bit long modulus
.................+++
.....+++
e is 65537 (0x10001)

# 使用私钥生成对应的公钥文件
❯ openssl rsa -in rsa-private-key.pem -pubout -out rsa-public-key.pem
writing RSA key

# 查看私钥内容
❯ cat rsa-private-key.pem
-----BEGIN RSA PRIVATE KEY-----
MIICXAIBAAKBgQDNE8QZLJZXREOeWZ2ilAzGC4Kjq/PfsFzrXGj8g3IaS4/J3JrB
o3qEq/k9XoRzOmNPyvWCj2FAY7A099d7qX4ztthBpUM2ePDIYDvhL0EpfQqbhe+Q
aagcFpuKTshGR2wBjH0Cl1/WxJkfIUMmWYU+m4iKLw9KfLX6BjmSgWB6HQIDAQAB
AoGADb5NXgKG8MI6ZdpLniGd2Yfb8WwMo+kF0SAYSRPmCa0WrciC9ocmJs3/ngU/
ixlWnnpTibRiKBaGMIaLglYRhvbvibUo8PH4woIidTho2e6swF2aqILk6YFJDpxX
FCFdbXM4Cm2MqbD4VtmhCYqbvuiyEUci83YrRP0jJGNt0GECQQDyZgdi8JlFQFH8
1QRHjLN57v5bHQamv7Qb77hlbdbg1wTYO+H8tsOB181TEHA7uN8hxkzyYZy+goRx
n0hvJcQXAkEA2JWhCb7oG1eal1aUdgofxhlWnkoFeWHay2zgDWSqmGKyDt0Cb1jq
XTdN9dchnqfptWN2/QPLDgM+/9g39/zv6wJATC1sXNeoE29nVMHNGn9JWCSXoyK4
GGdevvjTRm0Cfp6UUzBekQEO6Btd16Du5JXw6bhcLkAm9mgmH18jcGq5+QJBALnr
aDv3d0PRZdE372WMt03UfniOzjgueiVaJtMYcSEyx+reabKvvy+ZxACfVirdtU+S
PJhhYzN6MeBp+VGV/VUCQBXz0LyM08roWi6DiaRwJIbYx+WCKEOGXQ9QsZND+sGr
pOpugr3mcUge5dcZGKtsOUx2xRVmg88nSWMQVkTlsjQ=
-----END RSA PRIVATE KEY-----

# 查看私钥的详细参数
❯ openssl rsa -noout -text -in rsa-private-key.pem
Private-Key: (1024 bit)
modulus:
    0013:c4:19:2c:96:57:44:43:9e:59:9d:a2:94:
    0c:c6:0b:82:a3f3:df:b0:5c:eb:5c:68:fc:83:
    72:1a:4b:8f:c9:dc:9a:c1:a3:7a:84f9:3d:5e:
    84:73:3a:63:4f:ca:f5:82:8f:61:40:63:b0:34:f7:
    d7:7b:a9:7e:33:b6:d8:41:a5:43:36:78:f0:c8:60:
    3b:e1:2f:41:29:7d:0a:9b:85:ef:90:69:a8:1c:16:
    9b:8a:4e:c8:46:47:6c:01:8c:7d:02:97:5f:d6:c4:
    99:1f:21:43:26:59:85:3e:9b:88:8a:2f:0f:4a:7c:
    b5:fa:06:39:92:81:60:7a:1d
publicExponent: 65537 (0x10001)
privateExponent:
    0d:be:4d:5e:02:86:f0:c2:3a:65:da:4b:9e:21:9d:
    d9:87:db:f1:6c:0c:a3:e9:05:d1:20:18:49:13:e6:
    09:ad:16:ad:c8:82:f6:87:26:26:cd:ff:9e:05:3f:
    8b:19:56:9e:7a:53:89:b4:62:28:16:86:30:86:8b:
    82:56:11:86:f6:ef:89:b5:28:f0:f1:f8:c2:82:22:
    75:38:68:d9:ee:ac:c0:5d:9a:a8:82:e4:e9:81:49:
    0e:9c:57:14:21:5d:6d:73:38:0a:6d:8c:a9:b0:f8:
    56:d9:a1:09:8a:9b:be:e8:b2:11:47:22:f3:76:2b:
    44:fd:23:24:63:6d:d0:61
prime1:
    00:f2:66:07:62:f0:99:45:40:51:fc:d5:04:47:8c:
    b3:79:ee:fe:5b:1d:06:a6:bf:b4:1b:ef:b8:65:6d:
    d6:e0:d7:04:d8:3b:e1:fc:b6:c3:81:d7:cd:53:10:
    70:3b:b8:df:21:c6:4c:f2:61:9c:be:82:84:71:9f:
    48:6f:25:c4:17
prime2:
    00:d8:95:a1:09:be:e8:1b:57:9a:97:56:94:76:0a:
    1f:c6:19:56:9e:4a:05:79:61:da:cb:6c:e0:0d:64:
    aa:98:62:b2:0e:dd:02:6f:58:ea:5d:37:4d:f5:d7:
    21:9e:a7:e9:b5:63:76:fd:03:cb:0e:03:3e:ff:d8:
    37:f7:fc:ef:eb
exponent1:
    4c:2d:6c:5c:d7:a8:13:6f:67:54:c11a:7f:49:
    58:24:97:a3:22:b8:18:67:5e:be:f8:d3:46:6d:02:
    7e:9e:94:53:30:5e:91:01:0e:e8:1b:5d:d7:a0:ee:
    e4:95:f0:e9:b8:5c:2e:40:26:f6:68:26:1f:5f:23:
    70:6a:b9:f9
exponent2:
    00:b9:eb:68:3b:f7:77:43:d1:65:d1:37:ef:65:8c:
    b7:4d:d4:7e:78:8e:ce:38:2e:7a:25:5a:26:d3:18:
    71:21:32:c7:ea69:b2:af:bf:2f:99:c4:00:9f:
    56:2a:dd:b5:4f:92:3c:98:61:63:33:7a:31:e0:69:
    f9:51:95:fd:55
coefficient:
    15:f3:d0:bc:8c:d3:ca:e8:5a:2e:83:89:a4:70:24:
    86:d8:c7:e5:82:28:43:86:5d:0f:50:b1:93:43:fa:
    c1a4:ea:6e:82:bd:e6:71:48:1e:e5:d7:19:18:
    ab:6c:39:4c:76:c5:15:66:83:cf:27:49:63:10:56:
    44:e5:b2:34

# 查看私钥内容
❯ cat rsa-public-key.pem 
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDNE8QZLJZXREOeWZ2ilAzGC4Kj
q/PfsFzrXGj8g3IaS4/J3JrBo3qEq/k9XoRzOmNPyvWCj2FAY7A099d7qX4ztthB
pUM2ePDIYDvhL0EpfQqbhe+QaagcFpuKTshGR2wBjH0Cl1/WxJkfIUMmWYU+m4iK
Lw9KfLX6BjmSgWB6HQIDAQAB
-----END PUBLIC KEY-----

# 查看公钥的参数
❯ openssl rsa -noout -text -pubin -in rsa-public-key.pem
Public-Key: (1024 bit)
Modulus:
    0013:c4:19:2c:96:57:44:43:9e:59:9d:a2:94:
    0c:c6:0b:82:a3f3:df:b0:5c:eb:5c:68:fc:83:
    72:1a:4b:8f:c9:dc:9a:c1:a3:7a:84f9:3d:5e:
    84:73:3a:63:4f:ca:f5:82:8f:61:40:63:b0:34:f7:
    d7:7b:a9:7e:33:b6:d8:41:a5:43:36:78:f0:c8:60:
    3b:e1:2f:41:29:7d:0a:9b:85:ef:90:69:a8:1c:16:
    9b:8a:4e:c8:46:47:6c:01:8c:7d:02:97:5f:d6:c4:
    99:1f:21:43:26:59:85:3e:9b:88:8a:2f:0f:4a:7c:
    b5:fa:06:39:92:81:60:7a:1d
Exponent: 65537 (0x10001)

RSA 描述的私钥的结构如下（其中除 n,dn, dn,d 之外的都是冗余信息）：

modulus: 模数 nnn
publicExponent: 公指数 eee，固定为 65537 (0x10001)
privateExponent: 私钥指数 ddd
prime1: 质数 p，用于计算 nnn
prime2: 质数 q，用于计算 nnn
exponent1: 用于加速 RSA 运算的中国剩余定理指数一，dmod (p−1)d \mod (p-1)dmod(p−1)
exponent2: 用于加速 RSA 运算的中国剩余定理指数二，dmod (q−1)d \mod (q-1)dmod(q−1)
coefficient: 用于加速 RSA 运算的中国剩余定理系数，q−1mod pq^{-1} \mod pq−1modp

再看下 RSA 公钥的结构：

modulus: 模数 nnn
exponent: 公指数 eee，固定为 65537 (0x10001)

可以看到私钥文件中就已经包含了公钥的所有参数，实际上我们也是使用 openssl rsa -in rsa-private-key.pem -pubout -out rsa-public-key.pem 命令通过私钥生成出的对应的公钥文件。

下面就介绍下具体的密钥对生成流程，搞清楚 openssl 生成出的这个私钥，各项参数分别是什么含义：

这里不会详细介绍其中的各种数学证明，具体的请参考维基百科。相关数学知识包括取模运算的性质、欧拉函数、模倒数（拓展欧几里得算法）。


# pip install cryptography==36.0.1
from pathlib import Path
from cryptography.hazmat.primitives import serialization

key_path = Path("./rsa-private-key.pem")
private_key = serialization.load_pem_private_key(
    key_path.read_bytes(),
    password=None,
)
private = private_key.private_numbers()
public = private_key.public_key().public_numbers()
p = private.p
q = private.q
e = public.e
phi_n = (p-1) * (q-1)

def extended_euclidean(a, b):
    """
      拓展欧几里得算法，能在计算出 a 与 b 的最大公约数的同时，给出 ax + by = gcd(a, b) 中的 x 与 y 的值
      代码来自 wiki: https://zh.wikipedia.org/wiki/%E6%89%A9%E5%B1%95%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E7%AE%97%E6%B3%95
    """
    old_s, s = 1, 0
    old_t, t = 0, 1
    old_r, r = a, b
    if b == 0:
        return 1, 0, a
    else:
        while(r!=0):
            q = old_r // r
            old_r, r = r, old_r-q*r
            old_s, s = s, old_s-q*s
            old_t, t = t, old_t-q*t
    return old_s, old_t, old_r

# 我们只需要 d，y 可忽略，而余数 remainder 肯定为 1，也可忽略
d, y, remainder = extended_euclidean(e, phi_n)

n = p * q
print(f"{hex(n)=}")
# => hex(n)='0xcd13c4192c965744439e599da2940cc60b82a3abf3dfb05ceb5c68fc83721a4b8fc9dc9ac1a37a84abf93d5e84733a634fcaf5828f614063b034f7d77ba97e33b6d841a5433678f0c8603be12f41297d0a9b85ef9069a81c169b8a4ec846476c018c7d02975fd6c4991f21432659853e9b888a2f0f4a7cb5fa06399281607a1d'
print(f"{hex(d)=}")
# => hex(d)='0xdbe4d5e0286f0c23a65da4b9e219dd987dbf16c0ca3e905d120184913e609ad16adc882f6872626cdff9e053f8b19569e7a5389b46228168630868b82561186f6ef89b528f0f1f8c28222753868d9eeacc05d9aa882e4e981490e9c5714215d6d73380a6d8ca9b0f856d9a1098a9bbee8b2114722f3762b44fd2324636dd061'

对比 RSA 的输出，可以发现去掉冒号后，d 跟 n 的值是完全相同的。

RSA 加密与解密

RSA 解密运算的证明

这里的证明需要用到一些数论知识，觉得不容易理解的话，建议自行查找相关资料。

这样就证明了，解密操作得到的就是原始信息。

因为非对称加解密非常慢，对于较大的文件，通常会分成两步加密来提升性能：首先用使用对称加密算法来加密数据，再使用 RSA 等非对称加密算法加密上一步用到的「对称密钥」。

下面我们用 Python 来验证下 RSA 算法的加解密流程：

# pip install cryptography==36.0.1
from pathlib import Path
from cryptography.hazmat.primitives import serialization

# 私钥
key_path = Path("./rsa-private-key.pem")
private_key = serialization.load_pem_private_key(
    key_path.read_bytes(),
    password=None,
)
private = private_key.private_numbers()
public = private_key.public_key().public_numbers()
d = private.d

# 公钥
n = public.n
e = public.e

def int_to_bytes(x: int) -> bytes:
    return x.to_bytes((x.bit_length() + 7) // 8, 'big')

def int_from_bytes(xbytes: bytes) -> int:
    return int.from_bytes(xbytes, 'big')

def fast_power_modular(b: int, p: int, m: int):
    """
    快速模幂运算：b^p % m
    复杂度： O(log p)
    因为 RSA 的底数跟指数都非常大，如果先进行幂运算，最后再取模，计算结果会越来越大，导致速度非常非常慢
    根据模幂运算的性质  b^(ab) % m = (b^a % m)^b % m, 可以通过边进行幂运算边取模，极大地提升计算速度
    """
    res = 1
    while p:
        if p & 0x1: res *= b
        b = b ** 2 % m
        p >>= 1
    return res % m

# 明文
original_msg = b"an example"
print(f"{original_msg=}")

# 加密
msg_int = int_from_bytes(original_msg)
encrypt_int = msg_int ** e % n
encrypt_msg = int_to_bytes(encrypt_int)
print(f"{encrypt_msg=}")

# 解密
# decrypt_int = encrypt_int ** d % n # 因为 d 非常大，直接使用公式计算会非常非常慢，所以不能这么算
decrypt_int = fast_power_modular(encrypt_int, d, n)
decrypt_msg = int_to_bytes(decrypt_int)
print(f"{decrypt_msg=}")  # 应该与原信息完全一致

RSA 数字签名

前面证明了可以使用公钥加密，再使用私钥解密。

实际上从上面的证明也可以看出来，顺序是完全可逆的，先使用私钥加密，再使用公钥解密也完全是可行的。这种运算被我们用在数字签名算法中。

数字签名的方法为：

首先计算原始数据的 Hash 值，比如 SHA256
使用私钥对计算出的 Hash 值进行加密，得到数字签名
其他人使用公开的公钥进行解密出 Hash 值，再对原始数据计算 Hash 值对比，如果一致，就说明数据未被篡改

Python 演示：

# pip install cryptography==36.0.1
from hashlib import sha512
from pathlib import Path
from cryptography.hazmat.primitives import serialization

key_path = Path("./rsa-private-key.pem")
private_key = serialization.load_pem_private_key(
    key_path.read_bytes(),
    password=None,
)
private = private_key.private_numbers()
public = private_key.public_key().public_numbers()
d = private.d
n = public.n
e = public.e

# RSA sign the message
msg = b'A message for signing'
hash = int.from_bytes(sha512(msg).digest(), byteorder='big')
signature = pow(hash, d, n)
print("Signature:", hex(signature))

# RSA verify signature
msg = b'A message for signing'
hash = int.from_bytes(sha512(msg).digest(), byteorder='big')
hashFromSignature = pow(signature, e, n)
print("Signature valid:", hash == hashFromSignature)

4、ECC 密码系统

ECC 椭圆曲线密码学，于 1985 年被首次提出，并于 2004 年开始被广泛应用。 ECC 被认为是 RSA 的继任者，新一代的非对称加密算法。

其最大的特点在于相同密码强度下，ECC 的密钥和签名的大小都要显著低于 RSA. 256bits 的 ECC 密钥，安全性与 3072bits 的 RSA 密钥安全性相当。

其次 ECC 的密钥对生成、密钥交换与签名算法的速度都要比 RSA 快。

椭圆曲线的数学原理简介

在数学中，椭圆曲线（Elliptic Curves）是一种平面曲线，由如下方程定义的点的集合组成（A−J 均为常数）：

椭圆曲线大概长这么个形状：

椭圆曲线跟椭圆的关系，就犹如雷锋跟雷峰塔、Java 跟 JavaScript…

你可以通过如下网站手动调整 aaa 与 bbb 的值，拖动曲线的交点： Elliptic Curve Points

椭圆曲线上的运算

数学家在椭圆曲线上定义了一些运算规则，ECC 就依赖于这些规则，下面简单介绍下我们用得到的部分。

1. 加法与负元

对于曲线上的任意两点 AAA 与 BBB，我们定义过 A,B的直线与曲线的交点为 −(A + B)，而 −(A + B)相对于 x 轴的对称点即为 A+B：

上述描述一是定义了椭圆曲线的加法规则，二是定义了椭圆曲线上的负元运算。

2. 二倍运算

在加法规则中，如果 A = B，我们定义曲线在 A 点的切线与曲线的交点为 −2A，于是得到二倍运算的规则：

3. 无穷远点

4. k 倍运算

我们在前面已经定义了椭圆曲线上的加法运算、二倍运算以及无穷远点，有了这三个概念，我们就能定义k 倍运算 了。

5. 有限域上的椭圆曲线

椭圆曲线是连续且无限的，而计算机却更擅长处理离散的、存在上限的整数，因此 ECC 使用「有限域上的椭圆曲线」进行计算。

「有限域（也被称作 Galois Filed, 缩写为 GF）」顾名思义，就是指只有有限个数值的域。

ECDLP 椭圆曲线离散对数问题

前面已经介绍了椭圆曲线上的 k 倍运算 及相关的高效算法，但是我们还没有涉及到除法。

椭圆曲线上的除法是一个尚未被解决的难题——「ECDLP 椭圆曲线离散对数问题」：

已知 kG 与基点 G，求整数 k 的值。

椭圆曲线上的 k 倍运算与素数上的幂运算很类似，因此 ECC 底层的数学难题 ECDLP 与 RSA 的离散对数问题 DLP 也有很大相似性。

ECC 密钥对生成

首先，跟 RSA 一样，让我们先看下怎么使用 openssl 生成一个使用 prime256v1 曲线的 ECC 密钥对：

# 列出 openssl 支持的所有曲线名称
openssl ecparam -list_curves

# 生成 ec 算法的私钥，使用 prime256v1 算法，密钥长度 256 位。（强度大于 2048 位的 RSA 密钥）
openssl ecparam -genkey -name prime256v1 -out ecc-private-key.pem
# 通过密钥生成公钥
openssl ec -in ecc-private-key.pem -pubout -out ecc-public-key.pem

# 查看私钥内容
❯ cat ecc-private-key.pem
-----BEGIN EC PARAMETERS-----
BggqhkjOPQMBBw==
-----END EC PARAMETERS-----
-----BEGIN EC PRIVATE KEY-----
MHcCAQEEIGm3wT/m4gDaoJGKfAHDXV2BVtdyb/aPTITJR5B6KVEtoAoGCCqGSM49
AwEHoUQDQgAE5IEIorw0WU5+om/UgfyYSKosiGO6Hpe8hxkqL5GUVPyu4LJkfw/e
99zhNJatliZ1Az/yCKww5KrXC8bQ9wGQvw==
-----END EC PRIVATE KEY-----

# 查看私钥的详细参数
❯ openssl ec -noout -text -in ecc-private-key.pem
read EC key
Private-Key: (256 bit)
priv:
    69:b7:c1:3f:e6:e2:00:da:a0:91:8a:7c:01:c3:5d:
    5d:81:56:d7:72:6f:f6:8f:4c:84:c9:47:90:7a:29:
    51:2d
pub: 
    04:e4:81:08:a2:bc:34:59:4e:7e:a2:6f:d4:81:fc:
    98:48:aa:2c:88:63:ba:1e:97:bc:87:19:2a:2f:91:
    94:54:fc:ae:e0:b2:64:7f:0ff7:dc:e1:34:96:
    ad:96:26:75:03:3f:f2:08:ac:30:e4:aa:d7:0b:c6:
    d0:f7:01:90:bf
ASN1 OID: prime256v1
NIST CURVE: P-256

# 查看公钥内容
❯ cat ecc-public-key.pem 
-----BEGIN PUBLIC KEY-----
MFkwEwYHKoZIzj0CAQYIKoZIzj0DAQcDQgAE5IEIorw0WU5+om/UgfyYSKosiGO6
Hpe8hxkqL5GUVPyu4LJkfw/e99zhNJatliZ1Az/yCKww5KrXC8bQ9wGQvw==
-----END PUBLIC KEY-----

# 查看公钥的参数
❯ openssl ec -noout -text -pubin -in ecc-public-key.pem
read EC key
Private-Key: (256 bit)
pub: 
    04:e4:81:08:a2:bc:34:59:4e:7e:a2:6f:d4:81:fc:
    98:48:aa:2c:88:63:ba:1e:97:bc:87:19:2a:2f:91:
    94:54:fc:ae:e0:b2:64:7f:0ff7:dc:e1:34:96:
    ad:96:26:75:03:3f:f2:08:ac:30:e4:aa:d7:0b:c6:
    d0:f7:01:90:bf
ASN1 OID: prime256v1
NIST CURVE: P-256

可以看到 ECC 算法的公钥私钥都比 RSA 小了非常多，数据量小，却能带来同等的安全强度，这是 ECC 相比 RSA 最大的优势。

私钥的参数：

priv: 私钥，一个 256bits 的大整数，对应我们前面介绍的 k倍运算k倍运算k倍运算中的 k
pub: 公钥，是一个椭圆曲线（EC）上的坐标 x,y，也就是我们 well-known 的基点 G
ASN1 OID: prime256v1, 椭圆曲线的名称
NIST CURVE: P-256

使用安全随机数生成器即可直接生成出 ECC 的私钥 priv，因此 ECC 的密钥对生成速度非常快。

ECDH 密钥交换

ECC 加密与解密

ECC 本身并没有提供加密与解密的功能，但是我们可以借助 ECDH 迂回实现加解密。流程如下：

Bob 想要将消息 M 安全地发送给 Alice，他手上已经拥有了 Alice 的 ECC 公钥 alicePubKey
Bob 首先使用如下算法生成出「共享密钥」+「密文公钥」
- 随机生成一个临时 ECC 密钥对
  - 私钥：安全随机数 ciphertextPrivKey
  - 公钥：ciphertextPubKey = ciphertextPrivKey * G
- 使用 ECDH 计算出共享密钥：sharedECCKey = alicePubKey * ciphertextPrivKey
Bob 使用「共享密钥」与对称加密算法加密消息，得到密文 C
- 比如使用 AES-256-GCM 或者 ChaCha20-Poly1305 进行对称加密
Bob 将 C + ciphertextPubKey 打包传输给 Alice
Alice 使用 ciphertextPubKey 与自己的私钥计算出共享密钥 sharedECCKey = ciphertextPubKey * alicePrivKey
Alice 使用计算出的共享密钥解密 C 得到消息 M

实际上就是消息的发送方先生成一个临时的 ECC 密钥对，然后借助 ECDH 协议计算出共享密钥用于加密。消息的接收方同样通过 ECDH 协议计算出共享密钥再解密数据。

使用 Python 演示如下：

# pip install tinyec  # <= ECC 曲线库
from tinyec import registry
import secrets

# 使用这条曲线进行演示
curve = registry.get_curve('brainpoolP256r1')

def compress_point(point):
    return hex(point.x) + hex(point.y % 2)[2:]

def ecc_calc_encryption_keys(pubKey):
    """
    安全地生成一个随机 ECC 密钥对，然后按 ECDH 流程计算出共享密钥 sharedECCKey
    最后返回（共享密钥, 临时 ECC 公钥 ciphertextPubKey）
    """
    ciphertextPrivKey = secrets.randbelow(curve.field.n)
    ciphertextPubKey = ciphertextPrivKey * curve.g
    sharedECCKey = pubKey * ciphertextPrivKey
    return (sharedECCKey, ciphertextPubKey)

def ecc_calc_decryption_key(privKey, ciphertextPubKey):
    sharedECCKey = ciphertextPubKey * privKey
    return sharedECCKey

# 1. 首先生成出 Alice 的 ECC 密钥对
privKey = secrets.randbelow(curve.field.n)
pubKey = privKey * curve.g
print("private key:", hex(privKey))
print("public key:", compress_point(pubKey))

# 2. Alice 将公钥发送给 Bob

# 3. Bob 使用 Alice 的公钥生成出（共享密钥, 临时 ECC 公钥 ciphertextPubKey）
(encryptKey, ciphertextPubKey) = ecc_calc_encryption_keys(pubKey)
print("ciphertext pubKey:", compress_point(ciphertextPubKey))
print("encryption key:", compress_point(encryptKey))

# 4. Bob 使用共享密钥 encryptKey 加密数据，然后将密文与 ciphertextPubKey 一起发送给 Alice

# 5. Alice 使用自己的私钥 + ciphertextPubKey 计算出共享密钥 decryptKey
decryptKey = ecc_calc_decryption_key(privKey, ciphertextPubKey)
print("decryption key:", compress_point(decryptKey))

# 6. Alice 使用 decryptKey 解密密文得到原始消息

ECC 数字签名

前面已经介绍了 RSA 签名，这里介绍下基于 ECC 的签名算法。

基于 ECC 的签名算法主要有两种：ECDSA 与 EdDSA，以及 EdDSA 的变体。其中 ECDSA 算法稍微有点复杂，而安全强度跟它基本一致的 EdDSA 的算法更简洁更易于理解，在使用特定曲线的情况下 EdDSA 还要比 ECDSA 更快一点，因此现在通常更推荐使用 EdDSA 算法。

EdDSA 与 Ed25519 签名算法

EdDSA（Edwards-curve Digital Signature Algorithm）是一种现代的安全数字签名算法，它使用专为性能优化的椭圆曲线，如 255bits 曲线 edwards25519 和 448bits 曲线 edwards448.

EdDSA 签名算法及其变体 Ed25519 和 Ed448 在技术上在 RFC8032 中进行了描述。

首先，用户需要基于 edwards25519 或者 edwards448 曲线，生成一个 ECC 密钥对。生成私钥的时候，算法首先生成一个随机数，然后会对随机数做一些变换以确保安全性，防范计时攻击等攻击手段。对于 edwards25519 公私钥都是 32 字节，而对于 edwards448 公私钥都是 57 字节。

对于 edwards25519 输出的签名长度为 64 字节，而对于 Ed448 输出为 114 字节。

具体的算法虽然比 ECDSA 简单，但还是有点难度的，这里就直接略过了。

下面给出个 ed25519 的计算示例：

# pip install cryptography==36.0.1
from cryptography.hazmat.primitives.asymmetric.ed25519 import Ed25519PrivateKey

# 也可用 openssl 生成，都没啥毛病
private_key = Ed25519PrivateKey.generate()

# 签名
signature = private_key.sign(b"my authenticated message")

# 显然 ECC 的公钥 kG 也能直接从私钥 k 生成
public_key = private_key.public_key()
# 验证
# Raises InvalidSignature if verification fails
public_key.verify(signature, b"my authenticated message")

ed448 的代码也完全类似：

# pip install cryptography==36.0.1
from cryptography.hazmat.primitives.asymmetric.ed448 import Ed448PrivateKey

private_key = Ed448PrivateKey.generate()
signature = private_key.sign(b"my authenticated message")
public_key = private_key.public_key()
# Raises InvalidSignature if verification fails
public_key.verify(signature, b"my authenticated message")

密码学常用椭圆曲线介绍

在介绍密码学中的常用椭圆曲线前，需要先介绍一下椭圆曲线的阶（order）以及辅助因子（cofactor）这两个概念。

首先还得介绍下数学中「循环群」的概念，它是指能由单个元素所生成的群，在 ECC 中这就是预先定义好的基点 GGG.

一个有限域上的椭圆曲线可以形成一个有限「循环代数群」，它由曲线上的所有点组成。椭圆曲线的阶被定义为该曲线上所有点的个数（包括无穷远点）。

有些曲线加上 G 点可以形成一个单一循环群，这一个群包含了曲线上的所有点。而其他的曲线加上 G 点则形成多个不相交的循环子群，每个子群包含了曲线的一个子集。对于上述第二种情况，假设曲线上的点被拆分到了 h 个循环子群中，每个子群的阶都是 r，那这时整个群的阶就是 n=h∗r，其中子群的个数 h 被称为辅助因子。

举例如下：

secp256k1 的辅助因子为 1
Curve25519 的辅助因子为 8
Curve448 的辅助因子为 4

生成点 G

生成点 G 的选择是很有讲究的，虽然每个循环子群都包含有很多个生成点，但是 ECC 只会谨慎的选择其中一个。首先 G 点必须要能生成出整个循环子群，其次还需要有尽可能高的计算性能。

数学上已知某些椭圆曲线上，不同的生成点生成出的循环子群，阶也是不同的。如果 G 点选得不好，可能会导致生成出的子群的阶较小。前面我们已经提过子群的阶 rrr 会限制总的私钥数量，导致算法强度变弱！因此不恰当的 GGG 点可能会导致我们遭受「小子群攻击」。为了避免这种风险，建议尽量使用被广泛使用的加密库，而不是自己撸一个。

椭圆曲线的域参数

ECC椭圆曲线由一组椭圆曲线域参数描述，如曲线方程参数、场参数和生成点坐标。这些参数在各种密码学标准中指定，你可以网上搜到相应的 RFC 或 NIST 文档。

这些标准定义了一组命名曲线的参数，例如 secp256k1、P-521、brainpoolP512t1 和 SM2. 这些加密标准中描述的有限域上的椭圆曲线得到了密码学家的充分研究和分析，并被认为具有一定的安全强度。

也有一些密码学家（如 Daniel Bernstein）认为，官方密码标准中描述的大多数曲线都是「不安全的」，并定义了他们自己的密码标准，这些标准在更广泛的层面上考虑了 ECC 安全性。

开发人员应该仅使用各项标准文档给出的、经过密码学家充分研究的命名曲线。

secp256k1

此曲线被应用在比特币中，它的域参数如下：

p (modulus) = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
n (order; size; the count of all possible EC points) = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
a (方程 y2≡x3+a∗x+b(mod p)y^2 ≡ x^3 + a*x + b (\mod p)y2≡x3+a∗x+b(modp) 中的常数) = 0x0000000000000000000000000000000000000000000000000000000000000000
b (方程 y2≡x3+a∗x+b(mod p)y^2 ≡ x^3 + a*x + b (\mod p)y2≡x3+a∗x+b(modp) 中的常数)= 0x0000000000000000000000000000000000000000000000000000000000000007
g (the curve generator point G {x, y}) = (0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
h (cofactor, typically 1) = 01

Edwards 曲线

椭圆曲线方程除了我们前面使用的 Weierstrass 形式：

画个图长这样：

知名的 Edwards 曲线有：

Curve1174 (251-bit)
Curve25519 (255-bit)
Curve383187 (383-bit)
Curve41417 (414-bit)
Curve448 (448-bit)
E-521 (521-bit)
…

Curve25519, X25519 和 Ed25519

Ed25519 signing — Cryptography 38.0.0.dev1 documentation

Curve448, X448 和 Ed448

该选择哪种椭圆曲线？

首先，Bernstein 的 SafeCurves 标准列出了符合一组 ECC 安全要求的安全曲线，可访问 https://safecurves.cr.yp.to 了解此标准。

此外对于我们前面介绍的 Curve448 与 Curve25519，可以从性能跟安全性方面考量：

要更好的性能，可以接受弱一点的安全性：选择 Curve25519
要更好的安全性，可以接受比 Curve25519 慢 3 倍的计算速度：选择 Curve448

如果你的应用场景中暂时还很难用上 Curve448/Curve25519，你可以考虑一些应用更广泛的其他曲线，但是一定要遵守如下安全规范：

模数 p 应该至少有 256 位
- 比如 secp224k1 secp192k1 啥的就可以扫进历史尘埃里了
暂时没有想补充的，可以参考 https://safecurves.cr.yp.to

目前在 TLS 协议以及 JWT 签名算法中，目前应该最广泛的椭圆曲线仍然是 NIST 系列：

P-256: 到目前为止 P-256 应该仍然是应用最为广泛的椭圆曲线
- 在 openssl 中对应的名称为 prime256v1
P-384
- 在 openssl 中对应的名称为 secp384r1
P-521
- 在 openssl 中对应的名称为 secp521r1

但是我们也看到 Curve25519 正在越来越流行，因为美国政府有前科，NIST 标准被怀疑可能有后门，目前很多人都在推动使用 Curve25519 等社区方案取代掉 NIST 标准曲线。

对于 openssl，如下命令会列出 openssl 支持的所有曲线：

openssl ecparam -list_curves

ECIES - 集成加密方案

在文章开头我们已经介绍了集成加密方案 (IES)，它在密钥封装机制（KEM）的基础上，添加了密钥派生算法 KDF、消息认证算法 MAC 等其他密码学算法以达成我们对消息的安全性、真实性、完全性的需求。

而 ECIES 也完全类似，是在 ECC + 对称加密算法的基础上，添加了许多其他的密码学算法实现的。

ECIES 是一个加密框架，而不是某种固定的算法。它可以通过插拔不同的算法，形成不同的实现。比如「secp256k1 + Scrypt + AES-GCM + HMAC-SHA512」。

大概就介绍到这里吧，后续就请在需要用到时自行探索相关的细节咯。

八、数字证书与 TLS 协议

现代人的日常生活中，HTTPS 协议几乎无处不在，我们每天浏览网页时、用手机刷京东淘宝时、甚至每天秀自己绿色的健康码时，都在使用 HTTPS 协议。

作为一个开发人员，我想你应该多多少少有了解一点 HTTPS 协议。你可能知道 HTTPS 是一种加密传输协议，能保证数据传输的保密性。如果你拥有部署 HTTPS 服务的经验，那你或许还懂如何申请权威 HTTPS 证书，并配置在 Nginx 等 Web 程序上。

但是你是否清楚 HTTPS 是由 HTTP + TLS 两种协议组合而成的呢？更进一步你是否有抓包了解过 TLS 协议的完整流程？是否清楚它加解密的底层原理？是否清楚 Nginx 的 HTTPS 配置中一堆密码学参数的真正含义？是否知道 TLS 协议有哪些弱点、存在哪些攻击手段、如何防范？

接下来我们就深度剖析下 HTTPS 协议中的数字证书以及 TLS 协议。

1、数字证书与 PKI 公钥基础架构

我们在前面已经学习了「对称密码算法」与「非对称密码算法」两个密码学体系，这里做个简单的总结。

对称密码算法（如 AES/ChaCha20）: 计算速度快、安全强度高，但是缺乏安全交换密钥的手段、密钥的保存和管理也很困难。
非对称密码算法（如 RSA/ECC）: 计算速度慢，但是它解决了上述对称密码算法最大的两个缺陷，一是给出了安全的密钥交换算法 DHE/ECDHE，二呢它的公钥是可公开的，这降低了密钥的保存与管理难度。

但是非对称密码算法仍然存在一些问题:

公钥该如何分发？比如 Alice 跟 Bob 交换公钥时，如何确定收到的确实是对方的公钥，也就是说如何确认公钥的真实性、完整性、认证其来源身份？
- 前面我们已经学习过，DH/ECDH 密钥交换协议可以防范嗅探攻击（窃听），但是无法抵挡中间人攻击（中继）。
如果 Alice 的私钥泄漏了，她该如何作废自己旧的公钥？

数字证书与公钥基础架构就是为了解决上述问题而设计的。

首先简单介绍下公钥基础架构（Public Key Infrastructure），它是一组由硬件、软件、参与者、管理政策与流程组成的基础架构，其目的在于创造、管理、分配、使用、存储以及撤销数字证书。 PKI 是一个总称，而并非指单独的某一个规范或标准，因此显然数字证书的规范（X.509）、存储格式（PKCS系列标准、DER、PEM）、TLS 协议等都是 PKI 的一部分。

我们下面从公钥证书开始逐步介绍 PKI 中的各种概念及架构。

数字证书与 PKI 公钥基础架构

我们在前面已经学习了「对称密码算法」与「非对称密码算法」两个密码学体系，这里做个简单的总结。

对称密码算法（如 AES/ChaCha20）: 计算速度快、安全强度高，但是缺乏安全交换密钥的手段、密钥的保存和管理也很困难。
非对称密码算法（如 RSA/ECC）: 计算速度慢，但是它解决了上述对称密码算法最大的两个缺陷，一是给出了安全的密钥交换算法 DHE/ECDHE，二呢它的公钥是可公开的，这降低了密钥的保存与管理难度。

但是非对称密码算法仍然存在一些问题:

公钥该如何分发？比如 Alice 跟 Bob 交换公钥时，如何确定收到的确实是对方的公钥，也就是说如何确认公钥的真实性、完整性、认证其来源身份？
- 前面我们已经学习过，DH/ECDH 密钥交换协议可以防范嗅探攻击（窃听），但是无法抵挡中间人攻击（中继）。
如果 Alice 的私钥泄漏了，她该如何作废自己旧的公钥？

数字证书与公钥基础架构就是为了解决上述问题而设计的。

我们下面从公钥证书开始逐步介绍 PKI 中的各种概念及架构。

Google证书内容：

2. 证书链

前面介绍证书内容时，提到了每个证书都包含「签发者（Issuer）」信息，并且还包含「签发者」使用「证书内容」与「签发者私钥」生成的数字签名。

那么在证书交换时，如何验证证书的真实性、完整性及来源身份呢？根据「数字签名」算法的原理，显然需要使用「签发者公钥」来验证「被签发证书」中的签名。

仍然辛苦 Alice 与 Bob 来演示下这个流程:

假设现在 Alice 生成了自己的公私钥对，她想将公钥发送给远在千里之外的 Bob，以便与 Bob 进行加密通讯
但是如果 Alice 直接发送公钥给 Bob，Bob 并无法验证其来源是 Alice，也无法验证证书是否被篡改

PKI 引入了一个可信赖的第三者（Trusted third party，TTP）来解决这个问题。在 Alice 与 Bob 的案例中，就是说还有个第三者 Eve，他使用自己的私钥为自己的公钥证书签了名，生成了一个「自签名证书」，并且已经提前将这个「自签名证书」分发（比如当面交付、物理分发 emmm）给了 Alice 跟 Bob.

现在 Alice 首先使用自己的公钥以及个人信息制作了自己的公钥证书，但是这个证书还缺乏一个 Issuer 属性以及数字签名，我们把它叫做「证书签名请求（Certificate Signing Request, CSR）」
为了实现将证书安全传递给远在千里之外的 Bob，Alice 找到 Eve，将这个 CSR 文件提交给 Eve
Eve 验证了 Alice 的身份后，再使用这个 CSR 签发出完整的证书文件（Issuer 就填 Eve，然后 Eve 使用自己的私钥计算出证书的数字签名）交付给 Alice
- Eve 可是曾经跨越千里之遥，将自己的公钥证书分发给了 Bob，所以在给 Alice 签发证书时，他显然可能会要求付「签名费」。目前许多证书机构就是靠这个赚钱的，当然也有非盈利的证书机构如 Let’s Encrypt.
现在 Alice 再将经 Eve 签名的证书发送给 Bob
Bob 收到证书后，看到 Issuer 是 Eve，于是找出以前 Eve 给他的「自签名证书」，然后使用其中的公钥验证收到的证书
如果验证成功，就说明证书的内容是经过 Eve 认证的。如果 Eve 没老糊涂了，那这个证书应该确实就是 Alice 的。
如果验证失败，那说明这是某个攻击者伪造的证书。

在现实世界中，Eve 这个角色被称作「证书认证机构（Certification Authority, CA）」，全世界只有几十家这样的权威机构，它们都通过了各大软件厂商的严格审核，从而将根证书（CA 证书）直接内置于主流操作系统与浏览器中，也就是说早就提前分发给了因特网世界的几乎所有用户。由于许多操作系统或软件的更新迭代缓慢（2022 年了还有人用 XP 你敢信？），根证书的有效期通常都在十年以上。

但是，如果 CA 机构直接使用自己的私钥处理各种证书签名请求，这将是非常危险的。因为全世界有海量的 HTTPS 网站，也就是说有海量的证书需求，可一共才几十家 CA 机构。频繁的动用私钥会产生私钥泄漏的风险，如果这个私钥泄漏了，那将直接影响海量网站的安全性。

PKI 架构使用「数字证书链（也叫做信任链）」的机制来解决这个问题:

CA 机构首先生成自己的根证书与私钥，并使用私钥给根证书签名
- 因为私钥跟证书本身就是一对，因此根证书也被称作「自签名证书」
CA 根证书被直接交付给各大软硬件厂商，内置在主流的操作系统与浏览器中
然后 CA 机构再使用私钥签发一些所谓的「中间证书」，之后就把私钥雪藏了，非必要不会再拿出来使用。
- 通常离线存储在安全地点
- 中间层证书的有效期通常会比根证书短一些
- 部分中间证书会被作为备份使用，平常不会启用。
CA 机构使用这些中间证书的私钥，为用户提交的所有 CSR 请求签名

画个图来表示大概是这么个样子：

CA 机构也可能会在经过严格审核后，为其他机构签发中间证书，这样就能赋予其他机构签发证书的权利，而且根证书的安全性不受影响。

如果你访问某个 HTTPS 站点发现浏览器显示小绿锁，那就说明这个证书是由某个权威认证机构签发的，其信息是经过这些机构认证的。

上述这个全球互联网上，由证书认证机构、操作系统与浏览器内置的根证书、TLS 加密认证协议、OCSP 证书吊销协议等等组成的架构，我们可以称它为 Web PKI.

Web PKI 通常是可信的，但是并不意味着它们可靠。历史上出现过许多由于安全漏洞（2011 DigiNotar 攻击）或者政府要求，证书认证机构将假证书颁发给黑客或者政府机构的情况。获得假证书的人将可以随意伪造站点，而所有操作系统或浏览器都认为这些假站点是安全的，显示小绿锁。

因为证书认证机构的可靠性问题以及一些其他的原因，部分个人、企业或其他机构（比如金融机构）会生成自己的根证书与中间证书，然后自行签发证书，构建出自己的 PKI 认证架构，我们可以将它称作内部 PKI。但是这种自己生成的根证书是未内置在操作系统与浏览器中的，为了确保安全性，用户就需要先手动在设备上安装好这个数字证书。自行签发证书的案例有：

微信、支付宝及各种银行客户端中的数字证书与安全性更高的 USB 硬件证书（U 盾），这种涉及海量资金安全甚至国家安全的场景，显然是不能直接前面提到的几十个权威 CA 机构的。
局域网通信，通常是网络管理员生成一个本地 CA 证书安装到所有局域网设备上，再用它的私钥签发其他证书用于局域网安全通信
- 典型的例子是各企业的内部通讯网络，比如 Kubernetes 容器集群

现在再拿出前面 https://www.google.com 的证书截图看看，最上方有三个标签页，从左至右依次是「服务器证书」、「中间证书」、「根证书」，可以点进去分别查看这三个证书的各项参数，各位看官可以自行尝试。

Google 证书内容：

交叉签名

按前面的描述，每个权威认证机构都拥有一个正在使用的根证书，使用它签发出几个中间证书后，就会把它离线存储在安全地点，平常仅使用中间证书签发终端实体证书。这样实际上每个权威认证机构的证书都形成一颗证书树，树的顶端就是根证书。

实际上在 PKI 体系中，一些证书链上的中间证书会被使用多个根证书进行签名——我们称这为交叉签名。交叉签名的主要目的是提升证书的兼容性——客户端只要安装有其中任何一个根证书，就能正常验证这个中间证书。从而使中间证书在较老的设备也能顺利通过证书验证。

3. 证书的存储格式与编码标准

证书的格式这一块，是真的五花八门…沉重的历史包袱…

X509 只规定了证书应该包含哪些信息，但是未定义证书该如何存储。为了解决证书的描述与编码存储问题，又出现了如下标准：

ASN.1 结构：是一种描述证书格式的方法。
- 它类似 protobuf 数据描述语言、SQL DDL
- ASN.1 只规定了该如何描述证书，未定义该如何编码。
将 ASN.1 结构编码存储的格式有
- DER：一种二进制编码格式
- PEM：DER 是二进制格式，不便于复制粘贴，因此出现了 PEM，它是一个文本编码格式（其实就是把 DER 编码后的数据再 Base64 编码下…）
某些场景下，X.509 信息不够丰富，因此又设计了一些信息更丰富（例如可以包含证书链、秘钥）的证书封装格式，包括 PKCS #7 和 PKCS #12
- 仍然用 ASN.1 格式描述
- 基本都是用 DER 编码

下面详细介绍下这些相关的标准与格式。

编码存储格式 DER 与 PEM

DER 是由国际电信联盟（ITU）在 ITU-T X.690标准中定义的一种数据编码规则，用于将 ASN.1 结构的信息编码为二进制数据。直接以 DER 格式存储的证书，大都使用 .cer .crt .der 拓展名，在 Windows 系统比较常见。

而 PEM 格式，即 Privacy-Enhanced Mail，是 openssl 默认使用的证书格式。可用于编码公钥、私钥、公钥证书等多种密码学信息。 PEM 其实就是在 DER 的基础上多做一步——使用 Base64 将 DER 编码出的二进制数据再处理一次，编码成字符串再存储。好处是存储、传输要方便很多，可以直接复制粘贴。

一个 2048 位 RSA 公钥的 PEM 文件内容如下：

PEM 格式的数据通常以 .pem .key .crt .cer 等拓展名存储，直接 cat 一下是不是字符串，就能确认该文件是否是 PEM 格式了。

因为纯文本格式处理起来很方便，大部分场景下证书、公钥、私钥等信息都会被编码成 PEM 格式再进行存储、传输。

openssl 默认使用的输入输出均 PEM 格式。

PKCS#1

PKCS#1 是专用于编码 RSA 公私钥的标准，通常被编码为 PEM 格式存储。openssl 生成的 RSA 密钥对默认使用此格式。

这是一个比较陈旧的格式，openssl 之所以默认使用它，主要是为了兼容性。通常建议使用更安全的 PKCS#8 而不是这个。

一个使用 PKCS#1 标准的 2048 位 RSA 公钥文件，内容如下：

PKCS#7 / CMS

头疼… PKCS#7 导致是个啥玩意儿？为什么这么多五花八门的格式…

PKCS#7/CMS，是一个多用途的证书描述格式。它包含一个数据填充规则，这个填充规则常被用在需要数据填充的分组加密、数字签名等算法中。

另外据说 PKCS#7 也可以被用来描述证书，并以 DER/PEM 格式保存，后缀通常使用 .p7b 或者 .p7c, 这个暂时存疑吧，有需要再研究了。

PKCS#8

PKCS#8 是一个专门用于编码私钥的标准，可用于编码 DSA/RSA/ECC 私钥。它通常被编码成 PEM 格式存储。

前面介绍了专门用于编码 RSA 的 PKCS#1 标准比较陈旧，而且曾经出过漏洞。因此通常建议使用更安全的 PKCS#8 来取代 PKCS#1.

C# Java 等编程语言通常要求使用此格式的私钥，而 Python 的 pyca/cryptography 则支持多种编码格式。

一个非加密 ECC 私钥的 PKCS#8 格式如下：

一个加密 PKCS#8 私钥的 PEM 格式私钥如下：

-----BEGIN ENCRYPTED PRIVATE KEY-----
Base64 编码内容
-----END ENCRYPTED PRIVATE KEY-----

可使用如下 openssl 命令将 RSA/ECC 私钥转换为 PKCS#8 格式：

# RSA
openssl pkcs8 -topk8 -inform PEM -in rsa-private-key.pem -outform PEM -nocrypt -out rsa-private-key-pkcs8.pem

# ECC 的转换命令与 RSA 完全一致
openssl pkcs8 -topk8 -inform PEM -in ecc-private-key.pem -outform PEM -nocrypt -out ecc-private-key-pkcs8.pem

PKCS#12

PKCS#12 是一个归档文件格式，用于实现存储多个私钥及相关的 X.509 证书。

因为保存了私钥，为了安全性它通常是加密的，需要使用 passphrase 解密后才能使用。

PKCS#12 的常用拓展名为 .p12 .pfx.

PKCS#12 的主要使用场景是安全地保存、传输私钥及相关的 X.509 证书，比如：

微信/支付宝等支付相关的数字证书，通常使用 PKCS#12 格式存储，使用商户号做加密密码，然后编码为 base64 再提供给用户
安卓的 APK 签名证书通常使用 PKCS#12 格式存储，拓展名为 .keystore 或者 .jks.

PEM 格式转 PKCS#12（公钥和私钥都放里面）:

# 
openssl pkcs12 -export -in client.crt -inkey client.key -out client.p12
# 按提示输入保护密码

从 PKCS#12 中分别提取出 PEM 格式的公钥与私钥：

openssl pkcs12 -in xxx.p12 -out xxx.crt -clcerts -nokeys
openssl pkcs12 -in xxx.p12 -out xxx.key -nocerts -nodes

4. 证书支持保护的域名类型

TLS 证书支持配置多个域名，并且支持所谓的通配符（泛）域名。但是通配符域名证书的匹配规则，和 DNS 解析中的匹配规则并不一致！

根据证书选型和购买 - **阿里云文档的解释，通配符证书只支持同级匹配，详细说明如下:

一级通配符域名: 可保护该通配符域名（主域名）自身和该域名所有的一级子域名。
- 例如: 一级通配符域名 *.aliyun.com 可以用于保护 aliyun.com、www.aliyun.com 以及其他所有一级子域名。但是不能用于保护任何二级子域名，如 xx.aa.aliyun.com
二级或二级以上通配符域名: 只能保护该域名同级的所有通配域名，不支持保护该通配符域名本身。
- 例如: *.a.aliyun.com 只支持保护它的所有同级域名，不能用于保护三级子域名。

要想保护多个二三级子域，只能在生成 TLS 证书时，添加多个通配符域名。因此设计域名规则时，要考虑到这点，尽量不要使用层级太深的域名！有些信息可以通过 - 来拼接以减少域名层级，比如阿里云的 oss 域名:

公网: oss-cn-shenzhen.aliyuncs.com
内网: oss-cn-shenzhen-internal.aliyuncs.com

此外也可直接为 IP 地址签发证书，IP 地址可以记录在证书的 SAN 属性中。在自己生成的证书链中可以为局域网 IP 或局域网域名生成本地签名证书。此外在因特网中也有一些权威认证机构提供为公网 IP 签发证书的服务，一个例子是 Cloudflare 的 https://1.1.1.1, 使用 Firefox 查看其证书，可以看到是一个由 DigiCert 签发的 ECC 证书，使用了 P-256 曲线。

Cloudflare 的 IP 证书：

5. 生成自己的证书链

OpenSSL 是目前使用最广泛的网络加密算法库，这里以它为例介绍证书的生成。另外也可以考虑使用 CloudFalre 开源的 PKI 工具 cfssl.

前面介绍了，在局域网通信中通常使用本地证书链来保障通信安全，这通常有如下几个原因。

在内网环境下，管理员将本地 CA 证书安装到所有局域网设备上，因此并无必要向权威 CA 机构申请证书
内网环境使用的可能是非公网域名（xxx.local/xxx.lan/xxx.srv 等），甚至可能直接使用局域网 IP 通信，权威 CA 机构不签发这种类型的证书
本地证书链完全受自己控制，可以自己设置安全强度、证书年限等等，而且不受权威 CA 机构影响。
权威 CA 机构不签发客户端证书，因为客户端不一定有固定的 IP 地址或者域名。客户端证书需要自己签发。

下面介绍下如何使用 OpenSSL 生成一个本地 CA 证书链，并签发用于安全通信的服务端证书，可用于 HTTPS/QUIC 等协议。

1）生成 RSA 证书链

到目前为止 RSA 仍然是应用最广泛的非对称加密方案，几乎所有的根证书都是使用的 2048 位或者 4096 位的 RSA 密钥对。

对于 RSA 算法而言，越长的密钥能提供越高的安全性，当前使用最多的 RSA 密钥长度仍然是 2048 位，但是 2048 位已被一些人认为不够安全了，密码学家更建议使用 3072 位或者 4096 位的密钥。

生成一个 2048 位的 RSA 证书链的流程如下:

OpenSSL 的 CSR 配置文件官方文档: /docs/manmaster/man1/openssl-req.html

编写证书签名请求的配置文件 csr.conf：

[ req ]
prompt = no
default_md = sha256  # 在签名算法中使用 SHA-256 计算哈希值
req_extensions = req_ext
distinguished_name = dn

[ dn ]
C = CN  # Contountry
ST = Guangdong
L = Shenzhen
O = Xxx
OU = Xxx-SRE
CN = *.svc.local  # 泛域名，这个字段已经被 chrome/apple 弃用了。

[ alt_names ]  # 备用名称，chrome/apple 目前只信任这里面的域名。
DNS.1 = *.svc.local  # 一级泛域名
DNS.2 = *.aaa.svc.local  # 二级泛域名
DNS.3 = *.bbb.svc.local  # 二级泛域名

[ req_ext ]
subjectAltName = @alt_names

[ v3_ext ]
subjectAltName=@alt_names  # Chrome 要求必须要有 subjectAltName(SAN)
authorityKeyIdentifier=keyid,issuer:always
basicConstraints=CA:FALSE
keyUsage=keyEncipherment,dataEncipherment,digitalSignature
extendedKeyUsage=serverAuth,clientAuth

详情文档：OpenSSL file formats and conventions

生成证书链与服务端证书：

# 1. 生成本地 CA 根证书的私钥
openssl genrsa -out ca.key 2048
# 2. 使用私钥签发出 CA 根证书
## CA 根证书的有效期尽量设长一点，因为不方便更新换代，这里设了 100 年
openssl req -x509 -new -nodes -key ca.key -subj "/CN=MyLocalRootCA" -days 36500 -out ca.crt

# 3. 生成服务端证书的 RSA 私钥（2048 位）
openssl genrsa -out server.key 2048
# 4. 通过第一步编写的配置文件，生成证书签名请求（公钥+申请者信息）
openssl req -new -key server.key -out server.csr -config csr.conf
# 5. 使用 CA 根证书直接签发服务端证书，这里指定服务端证书的有效期为 3650 天
openssl x509 -req -in server.csr -CA ca.crt -CAkey ca.key \
  -CAcreateserial -out server.crt -days 3650 \
  -extensions v3_ext -extfile csr.conf

简单起见这里没有生成中间证书，直接使用根证书签发了用于安全通信的服务端证书。

2）生成 ECC 证书链

在上一篇文章中我们已经介绍过了，ECC 加密方案是新一代非对称加密算法，是 RSA 的继任者，在安全性相同的情况下，ECC 拥有比 RSA 更快的计算速度、更少的内存以及更短的密钥长度。

对于 ECC 加密方案而言，不同的椭圆曲线生成的密钥对提供了不同程度的安全性。各个组织（ANSI X9.62、NIST、SECG）命名了多种曲线，可通过如下命名查看 openssl 支持的所有椭圆曲线名称：

openssl ecparam -list_curves

目前在 TLS 协议以及 JWT 签名算法中，目前应该最广泛的椭圆曲线仍然是 NIST 系列：

P-256: 到目前为止 P-256 应该仍然是应用最为广泛的椭圆曲线
- 在 openssl 中对应的名称为 prime256v1
P-384
- 在 openssl 中对应的名称为 secp384r1
P-521
- 在 openssl 中对应的名称为 secp521r1

生成一个使用 P-384 曲线的 ECC 证书的示例如下:

编写证书签名请求的配置文件 ecc-csr.conf

[ req ]
prompt = no
default_md = sha256 # 在签名算法中使用 SHA-256 计算哈希值
req_extensions = req_ext
distinguished_name = dn

[ dn ]
C = CN  # Contountry
ST = Guangdong
L = Shenzhen
O = Xxx
OU = Xxx-SRE
CN = *.svc.local  # 泛域名，这个字段已经被 chrome/apple 弃用了。

[ alt_names ]  # 备用名称，chrome/apple 目前只信任这里面的域名。
DNS.1 = *.svc.local  # 一级泛域名
DNS.2 = *.aaa.svc.local  # 二级泛域名
DNS.3 = *.bbb.svc.local  # 二级泛域名

[ req_ext ]
subjectAltName = @alt_names

[ v3_ext ]
subjectAltName=@alt_names  # Chrome 要求必须要有 subjectAltName(SAN)
authorityKeyIdentifier=keyid,issuer:always
basicConstraints=CA:FALSE
keyUsage=keyEncipherment,dataEncipherment,digitalSignature
extendedKeyUsage=serverAuth,clientAuth

详情文档：OpenSSL file formats and conventions

2. 生成证书链与服务端证书：

# 1. 生成本地 CA 根证书的私钥，使用 P-384 曲线，密钥长度 384 位
openssl ecparam -genkey -name secp384r1 -out ecc-ca.key
# 2. 使用私钥签发出 CA 根证书
## CA 根证书的有效期尽量设长一点，因为不方便更新换代，这里设了 100 年
openssl req -x509 -new -nodes -key ecc-ca.key -subj "/CN=MyLocalRootCA" -days 36500 -out ecc-ca.crt

# 3. 生成服务端证书的 EC 私钥，使用 P-384 曲线，密钥长度 384 位
openssl ecparam -genkey -name secp384r1 -out ecc-server.key
# 4. 通过第一步编写的配置文件，生成证书签名请求（公钥+申请者信息）
openssl req -new -key ecc-server.key -out ecc-server.csr -config ecc-csr.conf
# 5. 使用 CA 根证书直接签发 ECC 服务端证书，这里指定服务端证书的有效期为 3650 天
openssl x509 -req -in ecc-server.csr -CA ecc-ca.crt -CAkey ecc-ca.key \
  -CAcreateserial -out ecc-server.crt -days 3650 \
  -extensions v3_ext -extfile ecc-csr.conf

简单起见这里没有生成中间证书，直接使用根证书签发了用于安全通信的服务端证书，而且根证书跟服务端证书都使用了 ECC 证书。现实中由于根证书更新缓慢，几乎所有的根证书都还是 RSA 证书，而中间证书与终端实体证书的迭代要快得多，目前已经有不少网站在使用 ECC 证书了。

6. 证书的类型

按照数字证书的生成方式进行分类，证书有三种类型:

由权威 CA 机构签名的「公网受信任证书」: 这类证书会被浏览器、小程序等第三方应用/服务商信任
- 申请证书时需要验证你对域名/IP 的所有权，也就使证书无法伪造
- 如果你的 API 需要提供给第三方应用/服务商/用户访问，那就需要向权威 CA 机构申请此类证书
本地签名证书 - tls_locally_signed_cert: 即由本地 CA 证书签名的 TLS 证书
- 本地 CA 证书，就是自己使用 openssl 等工具生成的 CA 证书
- 这类证书的缺点是无法与第三方应用/服务商建立安全的连接
- 如果客户端是完全可控的（比如是自家的 APP，或者是接入了域控的企业局域网设备），完全可以在所有客户端都安装上自己生成的 CA 证书。这种场景下使用此类证书是安全可靠的，可以不向权威 CA 机构申请证书
自签名证书 - tls_self_signed_cert: 前面介绍了根证书是一个自签名证书，它使用根证书的私钥为根证书签名
- 这里的「自签名证书」是指直接使用根证书进行网络通讯，缺点是证书的更新迭代会很麻烦，而且安全性低。

总的来说，权威CA机构颁发的「公网受信任证书」，可以被第三方应用信任，但是自己生成的不行。而越贵的权威证书，安全性与可信度就越高，或者可以保护更多的域名。

在客户端可控的情况下，可以考虑自己生成证书链并签发「本地签名证书」，将本地 CA 证书预先安装在客户端中用于验证。

而「自签名证书」主要是方便，能不用还是尽量不要使用。

7. 向权威 CA 机构申请「公网受信任证书」

向权威机构申请的公网受信任证书，可以直接应用在边界网关上，用于给公网用户提供 TLS 加密访问服务，比如各种 HTTPS 站点、API。这是需求最广的一类数字证书服务。

而证书的申请与管理方式又分为两种：

通过 ACMEv2（Automated Certificate Management Environment (ACME) 协议进行证书的自动化申请与管理。支持使用此开放协议申请证书的权威机构有：
- 免费服务
  - Let’s Encrypt: 众所周知，它提供三个月有效期的免费证书。
  - ZeroSSL: 貌似也是一个比较有名的 SSL 证书服务
    - 通过 ACME 协议支持不限数量的 90 天证书，也支持多域名证书与泛域名证书。
    - 它相比 Let’s Encrypt 的优势是，它提供一个证书控制台，可以查看与管理用户当前的所有证书，了解其状态。
- 付费服务
  - DigiCert: 这个非常有名（但也是相当贵），官方文档 Digicert - Third-party ACME client automation
  - Google Trust Services: Google 推出的公网证书服务，也是三个月有效期，其根证书交叉验证了 GlobalSign。官方文档 Automate Public Certificates Lifecycle Management via RFC 8555 (ACME)
  - Entrust: 官方文档 Entrust’s ACME implementation
  - GlobalSign: 官方文档 GlobalSign ACME Service
- 相关的自动化工具
  - 很多代理工具都有提供基于 ACMEv2 协议的证书申请与自动更新，比如:
    - Traefik
    - Caddy
    - docker-letsencrypt-nginx-proxy-companion
  - 网上也有一些 certbot 插件，可以通过 DNS 提供商的 API 进行 ACMEv2 证书的申请与自动更新，比如:
    - certbot-dns-aliyun
  - terraform 也有相关 provider: terraform-provider-acme
  - cert-manager: kubernetes 中的证书管理工具，支持 ACMEv2，也支持创建与管理私有证书。

通过一些权威 CA 机构或代理商提供的 Web 网站，手动填写信息来申请与更新证书。

这个流程相对会比较繁琐。

这些权威机构提供的证书服务，提供的证书又有不同的分级，这里详细介绍下三种不同的证书级别，以及该如何选用：

Domain Validated（DV）证书
- 仅验证域名所有权，验证步骤最少，价格最低，仅需要数分钟即可签发。
- 优点就是易于签发，很适合做自动化。
- 各云厂商（AWS/GCP/Cloudflare，以及 Vercel/Github 的站点服务）给自家服务提供的免费证书都是 DV 证书，Let’s Encrypt 的证书也是这个类型。
  - 很明显这些证书的签发都非常方便，而且仅验证域名所有权。
  - 但是 AWS/GCP/Cloudflare/Vercel/Github 提供的 DV 证书都仅能在它们的云服务上使用，不提供私钥功能！
Organization Validated (OV) 证书
- 是企业 SSL 证书的首选，通过企业认证确保企业 SSL 证书的真实性。
- 除域名所有权外，CA 机构还会审核组织及企业的真实性，包括注册状况、联系方式、恶意软件等内容。
- 如果要做合规化，可能至少也得用 OV 这个级别的证书。
Extended Validation（EV）证书
- 最严格的认证方式，CA 机构会深度审核组织及企业各方面的信息。
- 被认为适合用于大型企业、金融机构等组织或企业。
- 而且仅支持签发单域名、多域名证书，不支持签发泛域名证书，安全性杠杠的。

完整的证书申请流程如下:

为了方便用户，图中的申请人（Applicant）自行处理的部分，目前很多证书申请网站也可以自动处理，用户只需要提供相关信息即可。

8. 证书的寿命

对于公开服务，服务端证书的有效期不要超过 825 天（27 个月）！另外从 2020 年 11 月起，新申请的服务端证书有效期已经缩短到了 398 天（13 个月）。目前 Apple/Mozilla/Chrome 都发表了相应声明，证书有效期超过上述限制的，将被浏览器/Apple设备禁止使用。

而对于其他用途的证书，如果更换起来很麻烦，可以考虑放宽条件。比如 kubernetes 集群的加密证书，可以考虑有效期设长一些，比如 10 年。

据云原生安全破局｜如何管理周期越来越短的数字证书？所述，大量知名企业如特斯拉/微软/领英/爱立信都曾因未及时更换 TLS 证书导致服务暂时不可用。

因此 TLS 证书最好是设置自动轮转！人工维护不可靠！

目前很多 Web 服务器/代理，都支持自动轮转 Let’s Encrypt 证书。另外 Vault 等安全工具，也支持自动轮转私有证书。

9. 使用 OpenSSL 验证证书、查看证书信息

# 查看证书(crt)信息
openssl x509 -noout -text -in server.crt

# 查看证书请求(csr)信息
openssl req -noout -text -in server.csr

# 查看 RSA 私钥(key)信息
openssl rsa -noout -text -in server.key

# 验证证书是否可信
## 1. 使用系统的证书链进行验证
openssl verify server.crt
## 2. 使用指定的 CA 证书进行验证
openssl verify -CAfile ca.crt server.crt

2、TLS 协议

TLS 协议，中文名为「传输层安全协议」，是一个安全通信协议，被用于在网络上进行安全通信。

TLS 协议通常与 HTTP / FTP / SMTP 等协议一起使用以实现加密通讯，这种组合协议通常被缩写为 HTTPS / SFTP / SMTPS.

在讲 TLS 协议前，还是先复习下「对称密码算法」与「非对称密码算法」两个密码体系的特点。

对称密码算法（如 AES/ChaCha20）: 计算速度快、安全强度高，但是缺乏安全交换密钥的手段、密钥的保存和管理也很困难
非对称密码算法（如 RSA/ECC）: 解决了上述对称密码算法的两个缺陷——通过数字证书 + PKI 公钥基础架构实现了身份认证，再通过 DHE/ECDHE 实现了安全的对称密钥交换。

但是非对称密码算法要比对称密码算法更复杂，计算速度也慢得多。因此实际使用上通常结合使用这两种密码算法，各取其长，以实现高速且安全的网络通讯。我们通常称结合使用对称密码算法以及非对称密码算法的加密方案为「混合加密方案」。

TLS 协议就是一个「混合加密方案」，它借助数字证书与 PKI 公钥基础架构、DHE/ECDHE 密钥交换协议以及对称加密方案这三者，实现了安全的加密通讯。

基于经典 DHKE 协议的 TLS 握手流程如下：

而在支持「完美前向保密（Perfect Forward Secrecy）」的 TLS1.2 或 TLS1.3 协议中，经典 DH 协议被 ECDHE 协议取代。变化之一是进行最初的握手协议从经典 DHKE 换成了基于 ECC 的 ECDH 协议，变化之二是在每次通讯过程中也在不断地进行密钥交换，生成新的对称密钥供下次通讯使用。

TLS 协议通过应用 ECDHE 密钥交换协议，提供了「完美前向保密（Perfect Forward Secrecy）」特性，也就是说它能够保护过去进行的通讯不受密钥在未来暴露的威胁。即使攻击者破解出了一个「对称密钥」，也只能获取到一次事务中的数据，其他事务的数据安全性完全不受影响。

另外注意一点是，CA 证书和服务端证书都只在 TLS 协议握手的前三个步骤中有用到，之后的通信就与它们无关了。

1. 密码套件与 TLS 历史版本

密码套件（Cipher_suite）是 TLS 协议中一组用于实现安全通讯的密码学算法，类似于我们前面学习过的加密方案。不同密码学算法的组合形成不同的密码套件，算法组合的差异使这些密码套件具有不同的性能与安全性，另外 TLS 协议的更新迭代也导致各密码套件拥有不同的兼容性。通常越新推出的密码套件的安全性越高，但是兼容性就越差（旧设备不支持）。

密码套件的名称由它使用的各种密码学算法名称组成，而且有固定的格式，以 TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256 为例介绍下：

TLS: 定义了此套件适用的协议，通常固定为 TLS
ECDHE: 密钥交换算法
RSA: 数字证书认证算法
AES_128_GCM: 使用的对称加密方案，这是一个基于 AES 与 GCM 模式的对称认证加密方案，使用 128 位密钥
SHA256: 哈希函数，用于 HMAC 算法实现消息认证
- TLS 固定使用 HMAC 算法进行消息认证

TLS 协议的前身是 SSL 协议，TLS/SSL 的发展历程展示如下：

SSL 协议早在 2015 年就被各大主流浏览器废除了，TLS1.0 感觉也基本没站点在用了，这俩就直接跳过了。

下面分别介绍下 TLS1.1 TLS1.2 与 TLS1.3.

TLS 1.1

TLS 1.1 在 RFC4346 中定义，于 2006 年 4 月发布。

TLS 1.1 是 TLS 1.0 的一个补丁，主要更新包括：

添加对CBC攻击的保护
- 隐式初始向量 IV 被替换成一个显式的 IV
- 修复分组密码模式中填充算法的 bug
支持 IANA 登记的参数

TLS 1.1及其之前的算法曾经被广泛应用，它目前已知的缺陷如下：

不支持 PFS 完全前向保密
不支持 AEAD 认证加密算法
为了兼容性，保留了很多不安全的算法

TLS 1.1 已经不够安全了，不过一些陈年老站点或许还在使用它。

TLS 1.2

TLS 1.2 在 RFC5246 中定义，于 2008 年 8 月发发布。

可选支持 PFS 完全前向保密
移除对 MD5 与 SHA-1 签名算法的支持
添加对 HMAC-SHA-256 及 HMAC-SHA-384 消息认证算法的支持
添加对 AEAD 加密认证方案的支持
去除 forback 回到 SSL 协议的能力，提升安全性
为了兼容性，保留了很多不安全的算法

如果你使用 TLS 1.2，需要小心地选择密码套件，避开不安全的套件，就能实现足够高的安全性。

TLS 1.3

TLS 1.3 做了一次大刀阔斧的更新，是一个里程碑式的版本，其更新总结如下：

移除对如下算法的支持
- 哈希函数 SHA1/MD5
- 所有非 AEAD 加密认证的密码方案（CBC 模式）
- 移除对 RC4 与 3DES 加密算法的支持
- 移除了静态 RSA 与 DH 密钥交换算法
支持高性能的 Ed25519/Ed448 签名认证算法、X25519 密钥协商算法
支持高性能的 ChaCha20-Poly1305 对称认证加密方案
将密钥交换算法与公钥认证算法从密码套件中分离出来
- 比如原来的 TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256 密码套件将被拆分为 ECDHE 算法、RSA 身份认证算法、以及 TLS_AES_128_GCM_SHA256 密码套件
- 这样密码套件就只包含一个 AEAD 认证加密方案，以及一个哈希函数了
仅支持前向安全的密钥交换算法 DHE 或 ECDHE
支持最短 0-RTT 的 TLS 握手（会话恢复）

TLS 1.3 从协议中删除了所有不安全的算法或协议，可以说只要你的通讯用了 TLS 1.3，那你的数据就安全了（当然前提是你的私钥没泄漏）。

如何设置 TLS 协议的版本、密码套件参数

我们前面已经学习了对称加密、非对称加密、密钥交换三部分知识，对照 TLS 套件的名称，应该能很容易判断出哪些是安全的、哪些不够安全，哪些支持前向保密、哪些不支持。

一个非常好用的「站点 HTTPS 安全检测」网站是 SSL/TLS安全评估报告，使用它测试知乎网的检测结果如下：

能看到知乎为了兼容性，目前仍然支持 TLS1.0 与 TLS1.1，另外目前还不支持 TLS1.3.

此外，知乎仍然支持很多已经不安全的加密套件，myssl.com 专门使用黄色标识出了这些不安全的加密套件，我们总结下主要特征：

部分密码套件使用了不安全的对称加密算法 3DES
其他被标识为黄色的套件虽然使用了安全的对称加密算法，但是不支持 PFS 前向保密

此外 myssl.com 还列出了许多站点更详细的信息，包括 TLS1.3 的会话恢复，以及后面将会介绍的公钥固定、HTTP严格传输安全等信息：

Nginx 的 TLS 协议配置

以前为 Nginx 等程序配置 HTTPS 协议时，我最头疼的就是其中密码套件参数 ssl_ciphers，为了安全性，需要配置超长的一大堆选用的密码套件名称，我可以说一个都看不懂，但是为了把网站搞好还是得硬着头皮搜索复制粘贴，实际上也不清楚安全性导致咋样。

为了解决这个问题，Mozilla/DigitalOcean 都搞过流行 Web 服务器的 TLS 配置生成工具，比如 ssl-config - **mozilla，这个网站提供三个安全等级的配置**:

「Intermediate」: 查看生成出的 ssl-cipher 属性，发现它只支持 ECDHE/DHE 开头的算法。因此它保证前向保密。
- 对于需要通过浏览器访问的 API，推荐选择这个等级。
「Mordern」: 只支持 TLSv1.3，该协议废弃掉了过往所有不安全的算法，保证前向保密，安全性极高，性能也更好。
- 对于不需要通过浏览器等旧终端访问的 API，请直接选择这个等级。
「Old」: 除非你的用户使用非常老的终端进行访问，否则请不要考虑这个选项！

可以点进去查看详细的 TLS 套件配置。

OCSP 证书验证协议

How Do Browsers Handle Revoked SSL/TLS Certificates? - SSL.com

从无法开启 OCSP Stapling 说起 | JerryQu 的小站

SSL Certificate Checker - Diagnostic Tool | DigiCert.com

前面提到除了数字证书自带的有效期外，为了在私钥泄漏的情况下，能够吊销对应的证书，PKI 公钥基础设施还提供了 OCSP（Online Certificate Status Protocol）证书状态查询协议。

可以使用如下命令测试，确认站点是否启用了 ocsp stapling:

$ openssl s_client -connect www.digicert.com:443 -servername www.digicert.com -status -tlsextdebug < /dev/null 2>&1 | grep -i "OCSP response"

如果输出包含 OCSP Response Status: successful 就说明站点支持 ocsp stapling，如果输出内容为 OCSP response: no response sent 则说明站点不支持ocsp stapling。

实际上我测试发现只有 www.digicert.com/www.douban.com 等少数站点启用了 ocsp stapling，www.baidu.com/www.google.com/www.zhihu.com 都未启用 ocsp stapling.

这导致了一些问题：

Chrome/Firefox 等浏览器都会定期通过 OCSP 协议去请求 CA 机构的 OCSP 服务器验证证书状态，这可能会拖慢 HTTPS 协议的响应速度。
- 所谓的定期是指超过上一个 OCSP 响应的 nextUpdate 时间（一般为 7 天），或者如果该值为空的话，Firefox 默认 24h 后会重新查询 OCSP 状态。
因为客户端直接去请求 CA 机构的 OCSP 地址获取证书状态，这就导致 CA 机构可以获取到一些对应站点的用户信息（IP 地址、网络状态等）。

为了解决这两个问题，rfc6066 定义了 OCSP stapling 功能，它使服务器可以提前访问 OCSP 获取证书状态信息并缓存到本地，

在客户端使用 TLS 协议访问 HTTPS 服务时，服务端会直接在握手阶段将缓存的 OCSP 信息发送给客户端。因为 OCSP 信息会带有 CA 证书的签名及有效期，客户端可以直接通过签名验证 OCSP 信息的真实性与有效性，这样就避免了客户端访问 OCSP 服务器带来的开销。

ALPN 应用层协议协商

https://en.wikipedia.org/wiki/Application-Layer_Protocol_Negotiation

为什么我们应该尽快支持 ALPN？ | JerryQu 的小站

2. mTLS 双向认证

TLS 协议（tls1.0+，RFC: TLS1.2 - RFC5246）也定义了可选的服务端请求验证客户端证书的方法。这个方法是可选的。如果使用上这个方法，那客户端和服务端就会在 TLS 协议的握手阶段进行互相认证。这种验证方式被称为双向 TLS 认证(mTLS, mutual TLS)。

传统的「TLS 单向认证」技术，只在客户端去验证服务端是否可信。而「TLS 双向认证（mTLS）」，则添加了服务端验证客户端是否可信的步骤（第三步）:

客户端发起请求
「验证服务端是否可信」: 服务端将自己的 TLS 证书发送给客户端，客户端通过自己的 CA 证书链验证这个服务端证书。
「验证客户端是否可信」: 客户端将自己的 TLS 证书发送给服务端，服务端使用它的 CA 证书链验证该客户端证书。
协商对称加密算法及密钥
使用对称加密进行后续通信。

因为相比传统的 TLS，mTLS 只是添加了「验证客户端」这样一个步骤，所以这项技术也被称为「Client Authetication」.

mTLS 需要用到两套 TLS 证书:

服务端证书: 这个证书签名已经介绍过了。
客户端证书: 客户端证书貌似对证书信息（如 CN/SAN 域名）没有任何要求，只要证书能通过 CA 签名验证就行。

使用 openssl 生成 TLS 客户端证书（ca 和 csr.conf 可以直接使用前面生成服务端证书用到的，也可以另外生成）:

# 1. 生成 2048 位 的 RSA 密钥
openssl genrsa -out client.key 2048
# 2. 通过第一步编写的配置文件，生成证书签名请求
openssl req -new -key client.key -out client.csr -config csr.conf
# 3. 生成最终的证书，这里指定证书有效期 3650 天
### 使用前面生成的 ca 证书对客户端证书进行签名（客户端和服务端共用 ca 证书）
openssl x509 -req -in client.csr -CA ca.crt -CAkey ca.key \
   -CAcreateserial -out client.crt -days 3650 \
   -extensions v3_ext -extfile csr.conf

mTLS 的应用场景主要在「零信任网络架构」，或者叫「无边界网络」中。比如微服务之间的互相访问，就可以使用 mTLS。这样就能保证每个 RPC 调用的客户端，都是其他微服务（或者别的可信方），防止黑客入侵后为所欲为。

目前查到如下几个Web服务器/代理支持 mTLS:

Traefik: Docs - Client Authentication (mTLS)
Nginx: Using NGINX Reverse Proxy for client certificate authentication
1. 主要参数是两个: ssl_client_certificate /etc/nginx/client-ca.pem 和 ssl_verify_client on

mTLS 的安全性

如果将 mTLS 用在 App 安全上，存在的风险是:

客户端中隐藏的证书是否可以被提取出来，或者黑客能否 Hook 进 App 中，直接使用证书发送信息。
如果客户端私钥设置了「密码（passphrase）」，那这个密码是否能很容易被逆向出来？

mTLS 和「公钥锁定/证书锁定」对比:

公钥锁定/证书锁定: 只在客户端进行验证。
1. 但是在服务端没有进行验证。这样就无法鉴别并拒绝第三方应用（爬虫）的请求。
2. 加强安全的方法，是通过某种算法生成动态的签名。爬虫生成不出来这个签名，请求就被拒绝。
mTLS: 服务端和客户端都要验证对方。
1. 保证双边可信，在客户端证书不被破解的情况下，就能 Ban 掉所有的爬虫或代理技术。

3. 其他加密通讯协议

SSH 协议

首先最容易想到的应该就是是 SSH 协议（Secure SHell protocol）。SSH 与 TLS 一样都能提供加密通讯，是 PKI 公钥基础设施的早期先驱者之一。

OpenSSH 应用最广泛的 SSH 实现，它使用 SSH Key 而非数字证书进行身份认证，这主要是因为 OpenSSH 仅用于用户与主机之间的安全通信，不需要记录 X.509 这么繁多的信息。

我们来手动生成个 OpenSSH ed25519 密钥对试试（RSA 的生成命令完全类似）：

❯ ssh-keygen -t ed25519
Generating public/private ed25519 key pair.
Enter file in which to save the key (/Users/admin/.ssh/id_ed25519): ed25519-key
Enter passphrase (empty for no passphrase): 
Enter same passphrase again: 
Your identification has been saved in ed25519-key.
Your public key has been saved in ed25519-key.pub.
The key fingerprint is:
SHA256:jgeuWVflhNXXrDDzUtW6ZV1lpBWNAj0Rstizh9Lbyg0 [email protected]
The key's randomart image is:
+--[ED25519 256]--+
|          oo++ *%|
|         o =B ++B|
|        . = oO.+o|
|         . B. + +|
|      . S = o. + |
|     . + o +  .  |
|      + + E .    |
|     + o . +     |
|    o     o .    |
+----[SHA256]-----+

❯ cat ed25519-key    
-----BEGIN OPENSSH PRIVATE KEY-----
b3BlbnNzaC1rZXktdjEAAAAABG5vbmUAAAAEbm9uZQAAAAAAAAABAAAAMwAAAAtzc2gtZW
QyNTUxOQAAACDux4KnrKXVs4iR9mPZnSpur5207ceyMiZP+CDnXdooMQAAAKDnHOSY5xzk
mAAAAAtzc2gtZWQyNTUxOQAAACDux4KnrKXVs4iR9mPZnSpur5207ceyMiZP+CDnXdooMQ
AAAEADkVL1gZHAvBx4M5+UjVVL7ltVOC4r9tdR23CoI9iV1O7HgqespdWziJH2Y9mdKm6v
nbTtx7IyJk/4IOdd2igxAAAAHGFkbWluQHJ5YW4tTWFjQm9vay1Qcm8ubG9jYWwB
-----END OPENSSH PRIVATE KEY-----

❯ cat ed25519-key.pub 
ssh-ed25519 AAAAC3NzaC1lZDI1NTE5AAAAIO7HgqespdWziJH2Y9mdKm6vnbTtx7IyJk/4IOdd2igx [email protected]

可以看到 SSH Key 的结构非常简单，仅包含如下三个部分：

密钥对类型: 最常见的是 ssh-rsa，另外由于安全性目前更推荐使用 ssh-ed25519
公钥的 Base64 字符串
一个 Comment，通常包含这个 Key 的用途，或者 Key 所有者的邮箱地址

通过我们前面学的非对称密码学知识可以知道，公钥能直接从私钥生成，假设你的 ssh 公钥丢失，可以通过如下命令重新生成出公钥：

ssh-keygen -y -f xxx_rsa > xxx_rsa.pub

HTTP/3 与 QUIC 协议

QUIC 协议，是 Google 研发并推动标准化的 TCP 协议的替代品， QUIC 是基于 UDP 协议实现的。基于 QUIC 提出的 HTTP over QUIC 协议已被标准化为 RFC 9114 - HTTP/3，它做了很多大刀阔斧的改革：

传输层协议从 TCP 改成了 UDP，QUIC 自己实现的数据的可靠传输、按序到达、拥塞控制
- 也就是说 QUIC 绕过了陈旧的内核 TCP 协议实现，直接在用户空间实现了这些功能
- 通过另起炉灶，它解决了一些 TCP 协议的痛点：队头阻塞、握手延迟高、特性迭代慢、拥塞控制算法不佳等问题
在 TLS1.3 出现之前，QUIC 实现了自己的加密方案 QUIC Crypto 以取代陈旧的 TLS 协议，同时兼容现有的数字证书体系
- QUIC Crypto 的特点是它直接在应用层进行加密通讯的握手，并且恢复通信时可以通过缓存实现 0RTT 握手
- 也就说 QUIC 通过另起炉灶，解决了 TLS 的安全问题，以及握手延迟高的问题

总结一下就是，旧的实验性 HTTP-over-QUIC 协议，重新实现了 HTTP+TLS+TCP 三种协议并将它们整合到一起，这带来了极佳的性能，但也使它变得非常复杂。

QUIC 的 0RTT 握手是一个非常妙的想法，可以显著降低握手时延，TLS1.3 的设计者们将它纳入了 TLS1.3 标准中。

由于 TLS1.3 的良好特性，在 TLS1.3 协议发布后，新的 QUIC 标准 RFC 9001 已经使用 TLS1.3 取代了实验阶段使用的 QUIC Crypto 加密方案，目前只有 Chromium/Chrome 仍然支持 QUIC Crypto，其他 QUIC 实现基本都只支持 TLS1.3, 详见 QUIC Implementations.

4. TLS 协议攻防战

1. 证书锁定（Certifacte Pining）技术

即使使用了 TLS 协议对流量进行加密，并且保证了前向保密，也无法保证流量不被代理！

这是因为客户端大多是直接依靠了操作系统内置的 CA 证书库进行证书验证，而 Fiddler 等代理工具可以将自己的 CA 证书添加到该证书库中。

为了防止流量被 Fiddler 等工具使用上述方式监听流量，出现了「证书锁定（Certifacte Pining, 或者 SSL Pinning）」技术。方法是在客户端中硬编码证书的指纹（Hash值，或者直接保存整个证书的内容也行），在建立 TLS 连接前，先计算使用的证书的指纹是否匹配，否则就中断连接。

这种锁定方式需要以下几个前提才能确保流量不被监听:

客户端中硬编码的证书指纹不会被篡改。
指纹验证不能被绕过。
1. 目前有公开技术（XPosed+JustTrustMe）能破解 Android 上常见的 HTTPS 请求库，直接绕过证书检查。
2. 针对上述问题，可以考虑加大绕过的难度。或者 App 检测自己是否运行在 Xposed 等虚拟环境下。
用于 TLS 协议的证书不会频繁更换。（如果更换了，指纹就对不上了。）

而对于第三方的 API，因为我们不知道它们会不会更换 TLS 证书，就不能直接将证书指纹硬编码在客户端中。这时可以考虑从服务端获取这些 API 的证书指纹（附带私钥签名用于防伪造）。

为了实现证书的轮转(rotation)，可以在新版本的客户端中包含多个证书指纹，这样能保证同时有多个可信证书，达成证书的轮转。（类比 JWT 的公钥轮转机制）

证书锁定技术几乎等同于 SSH 协议的 StrictHostKeyChecking 选项，客户端会验证服务端的公钥指纹（key fingerprint），验证不通过则断开连接。

2. 公钥锁定（Public Key Pining）技术

前面介绍过证书的结构，它其实包含了公钥、有效期与一系列的其他信息。使用了证书锁定技术，会导致证书的有效期也被锁定，APK 内的证书指纹就必须随着证书一起更新。

更好的做法是指锁定证书中的公钥，即「公钥锁定」技术。「公钥锁定」比「证书锁定」更灵活，这样证书本身其实就可以直接轮转了（证书有过期时间），而不需要一个旧证书和新证书共存的中间时期。

「公钥锁定」是更推荐的锁定技术。

3. HTTPS 严格传输安全 - HSTS

HSTS，即 HTTP Strict Transport Security，是一项安全技术，它允许服务端在返回 HTTPS 响应时，通过 Headers 明确要求客户端，在之后的一段时间内必须使用安全的 HTTPS 协议访问服务端。

比如 https://example.com/ 的响应头中有 Strict-Transport-Security: max-age=31536000; includeSubDomains，表示服务端要求客户端（比如浏览器）：

在接下来的 31536000 秒（即一年）中，客户端向 example.com 或其子域名发送 HTTP 请求时，必须采用HTTPS来发起连接。
- 比如用户在浏览器地址栏输入 http://example.com/ 时，浏览器应自动将 http 改写为 https 再发起请求
在接下来的 31536000 秒（即一年）中，如果 example.com 服务器提供的证书无效，用户不能忽略浏览器的证书警告继续访问网站。
- 也就是说一旦证书失效，站点将完全无法访问，直至服务端修复证书问题。
- 一旦证书失效，HTTPS 其实就不是严格安全的了，可能会遭遇中间人攻击。

4. TLS 协议的逆向手段

要获取一个应用的 HTTPS 数据，有两个方向:

服务端入侵: 现代应用的服务端突破难度通常都比较客户端高，注入等漏洞底层框架就有处理。
1. 不过如果你获得了服务器 root 权限，可以在 openssl 上做文章，比如篡改 openssl？
客户端逆向+爬虫: 客户端是离用户最近的地方，也是最容易被突破的地方。
1. mTLS 常见的破解手段，是找到老版本的安装包，发现很容易就能提取出客户端证书。