【机器学习算法】关联规则2 FPgrowth法算法
FPgrowth算法
上次我们讲了关联规则里最有名的Apriori的算法,其中最重要的是它有两个瓶颈,第一个是它在产生候选项集的量可能会非常大,这个会占用我们的数据库,还有就是我们会多次扫描数据库,如果我们要产生长度为n关联规则,我们至少要扫描N+1次的数据库。多一次是因为那一次可能不会产生任何的频繁项集。
这样会很浪费时间。
于是就有学者提出了FPGrowth的方法,好处就是可以并行的处理频繁项目的产生。
举个例子
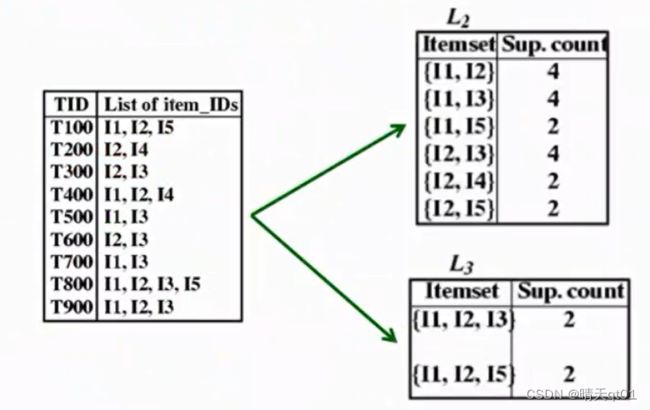
上面这个是我们用Apriori的方法得出的结果。
如果我们使用的是FPgrowth的方法,就会产生下面的情况
我能对应的去看的话,它的结果其实和Apriori的方法产生的结果是相同的。但是他是分别产生I5,I3,I4,I1。它没有说那个要先执行,哪些要后执行,可以并行运算,而且它不需要扫描数据库多次,只要扫描数据库2次
下面我们说说FPgrows是如何去运作的。
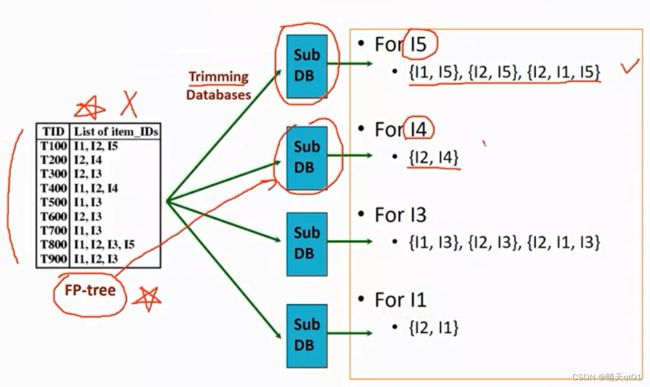
首先它会把交易数据库建成一个Fp-tree,之后就不再扫描交易数据库,然后我们会对这个FP-tree进行处理,去找它的子树,
我们就可以通过这个寻找到trimming sub DB
举个案例:
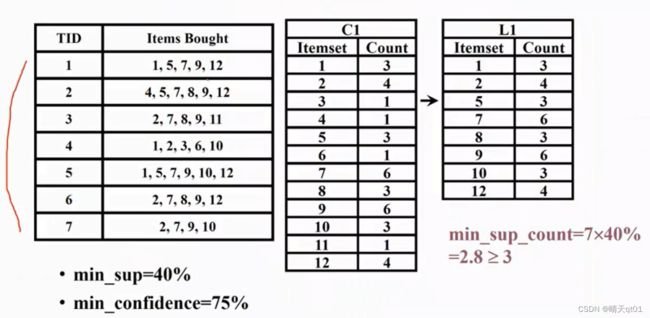
比如这个,第一个表格的第一行记录是1,5,7,9,12代表的是这笔数据它购买了1,5,7,9,12六项产品的交易。一次类推
假设我们制定最小支持度为百分之40,那最小支持度的最小支持的次数也就是2.8。也就是最少7笔数据出现3次,才是我们的频繁项目, 这里面我们就发现,1,2,5,7,9,10,12.
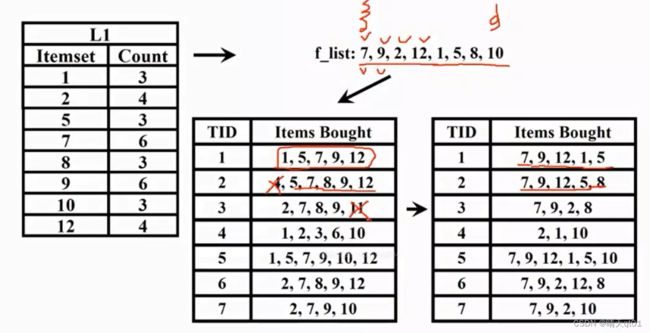
然后我们对它们按出现的次数进行排序。
由大到小的排序结果如上,我们建立这个FPtree的时候,我们需要建立一个比较精简的FPtree,
我们要将原始的数据库按照这个顺序排序,然后把已经没有出现的商品,进行排除。
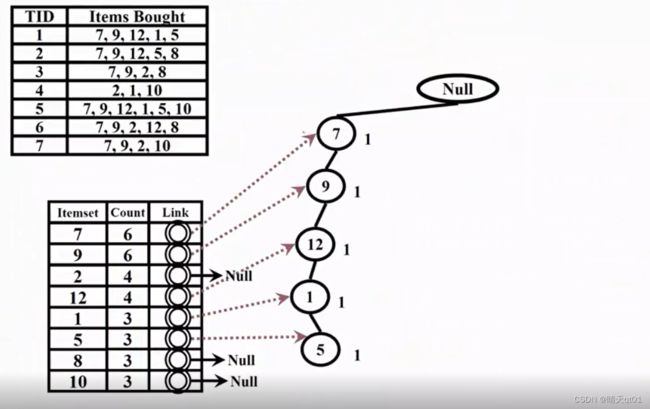
右下角就是我们表格
第一次扫描得到每个商品的次数,第二次扫描得到FP-tree
我们按照左上角的原始数据表格,把每一笔交易记录,读进数据,虚线代表它通过最小支持度了。这里读的就是第一笔交易记录,其中交易过的每个商品交易记录为1
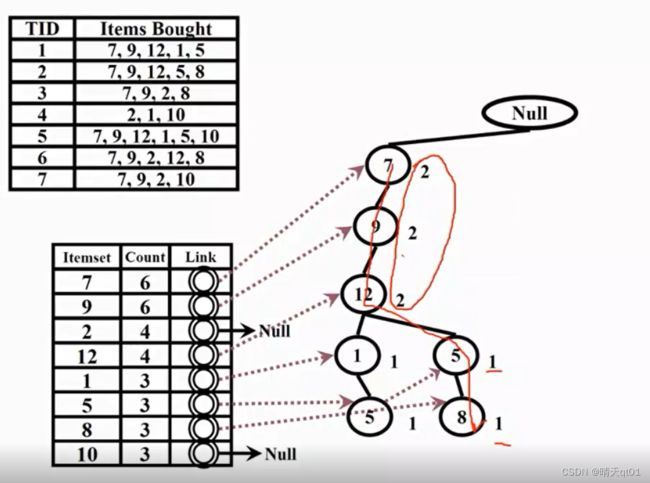
第二笔就得记入为上图情况,如果在这个位置有,就直接重复次数加1,如果没有的话,就新串一个子叶,比如5在第4个位置不存在,就新串一个,虚线代表相同数字横向连接
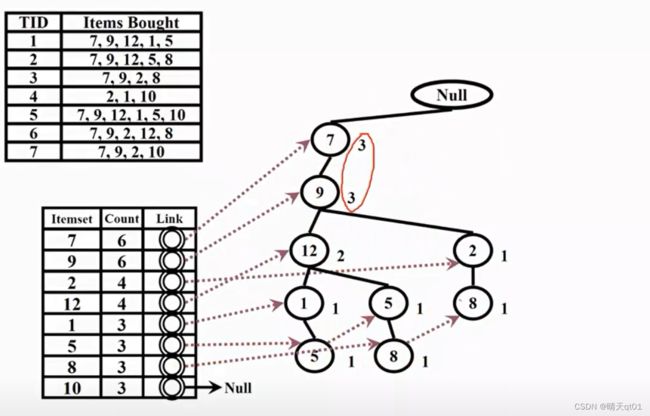
第4笔数据,因为2作为第一笔数据,是新的情况,就串一个新子树
第6笔数据也会出现新子树
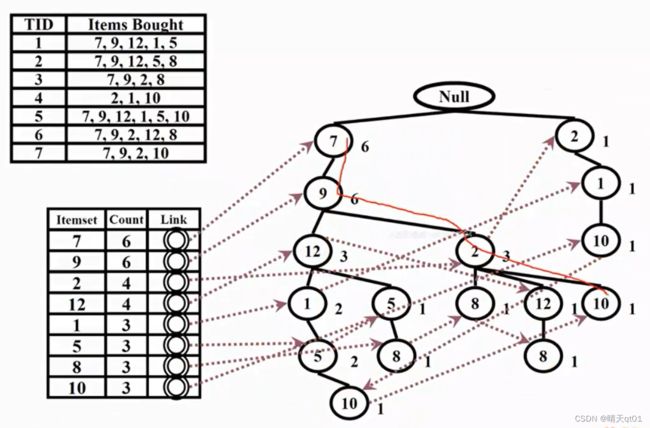
这个就是我们建立的FP-tree,如果一个数字对应的次数越多,说明它越容易与其他子树共用分支
这个树会比较精简,比较不占用内存。交易数据库就可以扔掉了,所有的信息都在这个FP-tree
现在我们就要开始产生我们的频繁项目集。
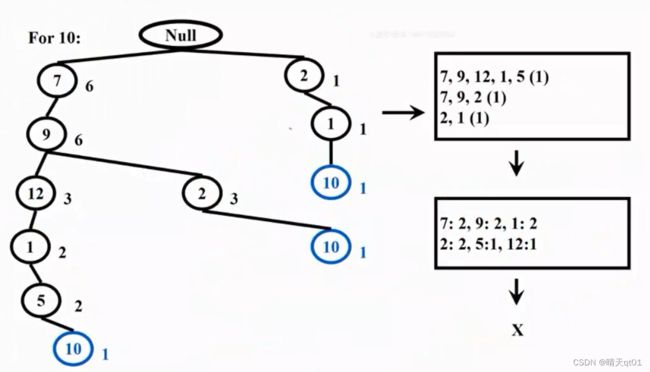
For 10
我们就会列出:
这个就是产品10的3个序列。因为我们最后都是10,就可以不用管。得到右上角的表格。对应的次数都是一次。
我们在生成其中每个水平出现的次数表格右下角:
7出现2次,9出现2次,1出现2次。因为我们最小次数需要出现3次,所以就没有任何频繁项目集的出现。
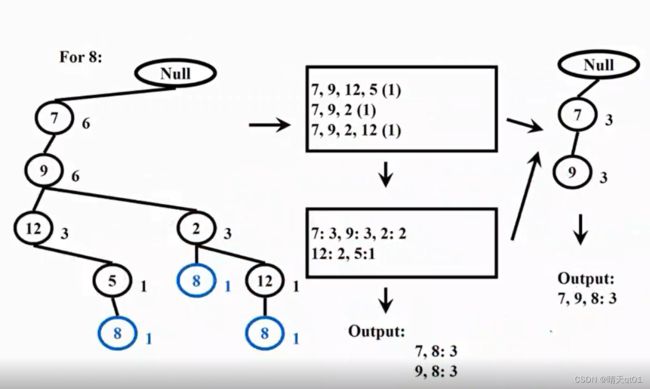
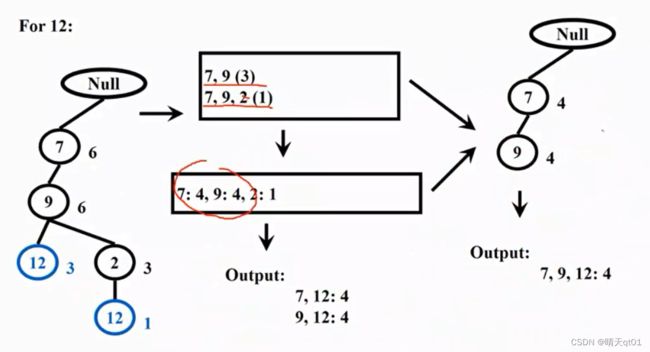
For8
同样的,我们产生8的部分的子树图
我们计算每个商品出现的次数,就会发现,7,9,的次数超过3,那么我们就可以建立程度为2的频繁项目
并且我们还可以再画一个fptree,得到长度为3的频繁项目。
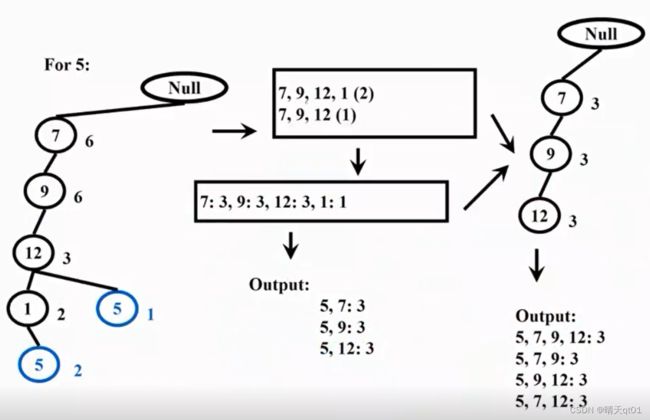
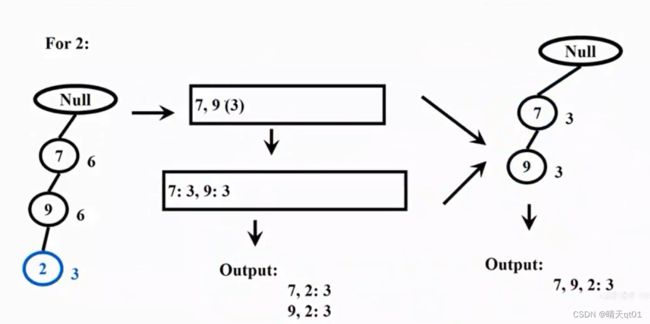
For 5
一样的,按步骤我们得到每个商品的次数,然后得到新子树,然后两两搭配。
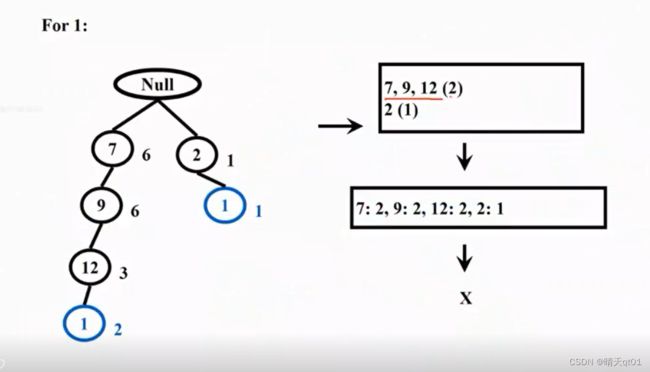
For1
所以1没有频繁项目产生。
这就是FPgrowth,他可以根据不同的产品产生频繁项目,而且可以并行产生频繁项目,速度快,而且只要扫描数据库2次。是因为它产生了一个FP-tree储存起来,就可以不用多次扫描了。