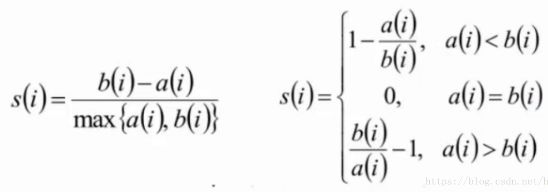机器学习算法(十二):聚类(3)基于密度的聚类——DBSCAN聚类算法
目录
1 DBSCAN聚类算法
2 参数选择
3 步骤
4 实例
5 常用的评估方法:轮廓系数
6 DBSCAN 算法评价及改进
基于密度的聚类是根据样本的密度分布来进行聚类。通常情况下,密度聚类从样本密度的角度出来,来考查样本之间的可连接性,并基于可连接样本不断扩展聚类簇,以获得最终的聚类结果。其中最著名的算法就是 DBSCAN 算法。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种基于密度的空间聚类算法。 该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇,它将簇定义为密度相连的点的最大集合。
1 DBSCAN聚类算法
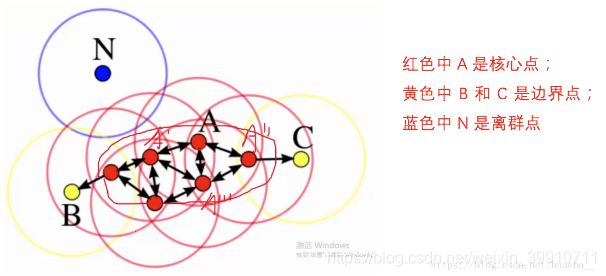
如下图所示,下面这些点是分布在样本空间的众多样本,现在我们的目标是把这些在样本空间中距离相近的聚成一类。我们发现A点附近的点密度较大,红色的圆圈根据一定的规则在这里滚啊滚,最终收纳了A附近的5个点,标记为红色也就是定为同一个簇。其它没有被收纳的根据一样的规则成簇。(形象来说,我们可以认为这是系统在众多样本点中随机选中一个,围绕这个被选中的样本点画一个圆,规定这个圆的半径以及圆内最少包含的样本点,如果在指定半径内有足够多的样本点在内,那么这个圆圈的圆心就转移到这个内部样本点,继续去圈附近其它的样本点,类似传销一样,继续去发展下线。等到这个滚来滚去的圈发现所圈住的样本点数量少于预先指定的值,就停止了。那么我们称最开始那个点为核心点,如A,停下来的那个点为边界点,如B、C,没得滚的那个点为离群点,如N)。
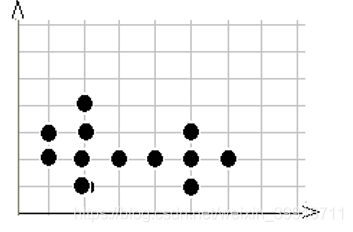
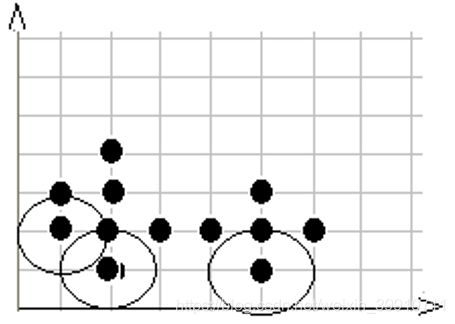
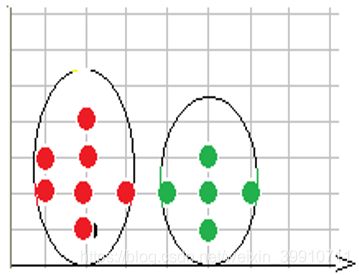
基于密度这点有什么好处呢,我们知道kmeans聚类算法只能处理球形的簇,也就是一个聚成实心的团(这是因为算法本身计算平均距离的局限)。但往往现实中还会有各种形状,比如下面两张图,环形和不规则形,这个时候,那些传统的聚类算法显然就悲剧了。于是就思考,样本密度大的成一类,就是DBSCAN聚类算法。
2 参数选择
上面提到了红色圆圈滚啊滚的过程,这个过程就包括了DBSCAN算法的两个参数:半径 eps 和密度阈值 MinPts。
(1)半径:半径是最难指定的 ,大了,圈住的就多了,簇的个数就少了;反之,簇的个数就多了,这对我们最后的结果是有影响的。我们这个时候K距离可以帮助我们来设定半径r,也就是要找到突变点,比如:

以上虽然是一个可取的方式,但是有时候比较麻烦 ,大部分还是都试一试进行观察,用k距离需要做大量实验来观察,很难一次性把这些值都选准。
(2)MinPts:这个参数就是圈住的点的个数,也相当于是一个密度,一般这个值都是偏小一些,然后进行多次尝试
国外有一个特别有意思的网站:Visualizing DBSCAN Clustering,它可以把我们DBSCAN的迭代过程动态图画出来。
3 步骤
- 以每一个数据点 xi 为圆心,以 eps 为半径画一个圆圈。这个圆圈被称为 xi 的 eps 邻域
- 对这个圆圈内包含的点进行计数。如果一个圆圈里面的点的数目超过了密度阈值 MinPts,那么将该圆圈的圆心记为核心点,又称核心对象。如果某个点的 eps 邻域内点的个数小于密度阈值但是落在核心点的邻域内,则称该点为边界点。既不是核心点也不是边界点的点,就是噪声点。
- 核心点 xi 的 eps 邻域内的所有的点,都是 xi 的直接密度直达。如果 xj 由 xi 密度直达,xk 由 xj 密度直达。。。xn 由 xk 密度直达,那么,xn 由 xi 密度可达。这个性质说明了由密度直达的传递性,可以推导出密度可达。
- 如果对于 xk,使 xi 和 xj 都可以由 xk 密度可达,那么,就称 xi 和 xj 密度相连。将密度相连的点连接在一起,就形成了我们的聚类簇。
用更通俗易懂的话描述就是如果一个点的 eps 邻域内的点的总数小于阈值,那么该点就是低密度点。如果大于阈值,就是高密度点。如果一个高密度点在另外一个高密度点的邻域内,就直接把这两个高密度点相连,这是核心点。如果一个低密度点在高密度点的邻域内,就将低密度点连在距离它最近的高密度点上,这是边界点。不在任何高密度点的 eps 邻域内的低密度点,就是异常点。
- 噪声: 一个基于密度的簇是基于密度可达性的最大的密度相连对象的集合。不包含在任何簇中的对象被认为是“噪声”
- 边界点:边界点不是核心点,但落在某个核心点的邻域内。
周志华《机器学习》书上给的伪代码如下。
![]()
公式性有点强,用语义表达算法的伪码如下:
- 根据 eps 邻域和密度阈值 MinPts ,判断一个点是核心点、边界点或者离群点。并将离群点删除
- 如果核心点之间的距离小于 MinPts ,就将两个核心点连接在一起。这样就形成了若干组簇
- 将边界点分配到距离它最近的核心点范围内
- 形成最终的聚类结果
4 实例
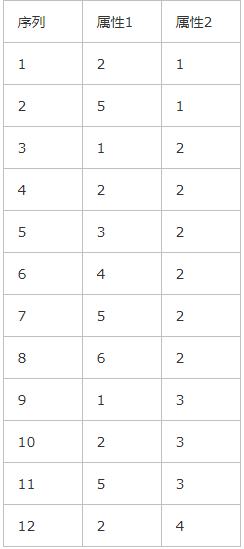
根据所给的数据通过对其进行DBSCAN算法,以下为算法的步骤(设n=12,用户输入ε=1,MinPts=4)
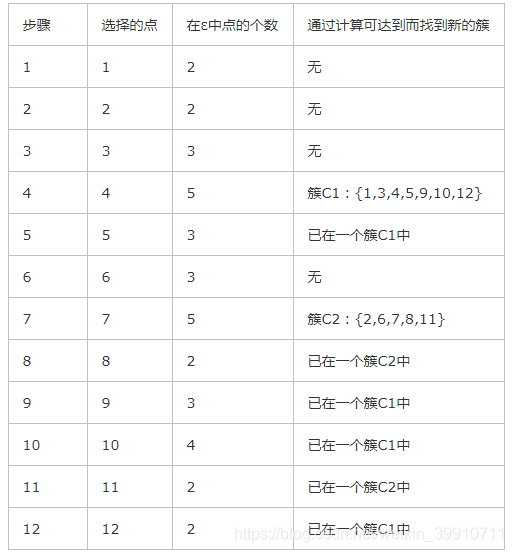
DBSCAN聚类过程
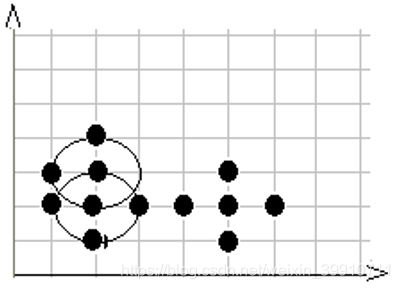
第1步,在数据库中选择一点1,由于在以它为圆心的 以1为半径的圆内包含2个点(小于4),因此它不是核心点,选择下一个点。
第2步,在数据库中选择一点2,由于在以它为圆心的,以1为半径的圆内包含2个点, 因此它不是核心点,选择下一个点。
第3步,在数据库中选择一点3,由于在以它为圆心的,以1为半径的圆内包含3个点, 因此它不是核心点,选择下一个点。
第4步,在数据库中选择一点4,由于在以它为圆心的,以1为半径的圆内包含5个点, 因此它是核心点,寻找从它出发可达的点(直接可达4个,间接可达3个), 聚出的新类{1,3,4,5,9,10,12},选择下一个点。
第5步,在数据库中选择一点5,已经在簇1中,选择下一个点。
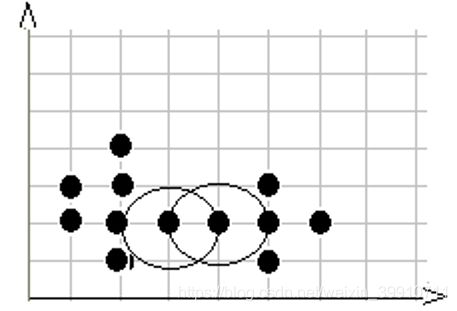
第6步,在数据库中选择一点6,由于在以它为圆心的,以1为半径的圆内包含3个点, 因此它不是核心点,选择下一个点。
第7步,在数据库中选择一点7,由于在以它为圆心的,以1为半径的圆内包含5个点, 因此它是核心点,寻找从它出发可达的点,聚出的新类{2,6,7,8,11},选择下一个点。
第8步,在数据库中选择一点8,已经在簇2中,选择下一个点。
第9步,在数据库中选择一点9,已经在簇1中,选择下一个点。
第10步,在数据库中选择一点10,已经在簇1中,选择下一个点。
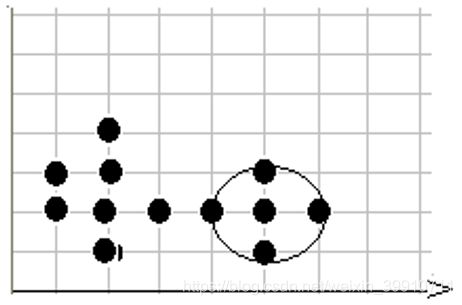
第11步,在数据库中选择一点11,已经在簇2中,选择下一个点。
第12步,选择12点,已经在簇1中,由于这已经是最后一点所有点都以处理,程序终止。
算法执行过程:
5 常用的评估方法:轮廓系数
聚类算法中最常用的评估方法——轮廓系数(Silhouette Coefficient):
计算样本i到同簇其它样本到平均距离ai。ai越小,说明样本i越应该被聚类到该簇(将ai称为样本i到簇内不相似度)。
计算样本i到其它某簇Cj的所有样本的平均距离bij,称为样本i与簇Cj的不相似度。定义为样本i的簇间不相似度: bi=min(bi1,bi2,...,bik2)
- si接近1,则说明样本i聚类合理
- si接近-1,则说明样本i更应该分类到另外的簇
- 若si近似为0,则说明样本i在两个簇的边界上
6 DBSCAN 算法评价及改进
DBSCAN优点:
1、对噪声不敏感。这是因为该算法能够较好地判断离群点,并且即使错判离群点,对最终的聚类结果也没什么影响
2、能发现任意形状的簇。这是因为DBSCAN 是靠不断连接邻域呢高密度点来发现簇的,只需要定义邻域大小和密度阈值,因此可以发现不同形状,不同大小的簇
DBSCAN 缺点:
1、对两个参数的设置敏感,即圈的半径 eps 、阈值 MinPts。
2、DBSCAN 使用固定的参数识别聚类。显然,当聚类的稀疏程度不同,聚类效果也有很大不同。即数据密度不均匀时,很难使用该算法
3、如果数据样本集越大,收敛时间越长。此时可以使用 KD 树优化
DBSCAN的时间复杂性:
DBSCAN算法要对每个数据对象进行邻域检查时间性能较低。DBSCAN的基本时间复杂度是 O(N*找出Eps领域中的点所需要的时间), N是点的个数。 最坏情况下时间复杂度是O(N2)在低维空间数据中,有一些数据结构如KD树,使得可以有效的检索特定点给定距离内的所有点, 时间复杂度可以降低到O(NlogN)。
DBSCAN的空间复杂性:
在聚类过程中,DBSCAN一旦找到一个核心对象,即以该核心对象为中心向外扩展。 此过程中核心对象将不断增多,未处理的对象被保留在内存中。若数据库中存在庞大的聚类, 将需要很大的存来存储核心对象信息,其需求难以预料。当数据量增大时,要求较大的内存支持 I/0 消耗也很大;低维或高维数据中,其空间都是O(N)。
常用聚类算法(基于密度的聚类算法 - StormTides - 博客园
聚类算法(三)——基于密度的聚类算法(以 DBSCAN 为例)_dengheCSDN的博客-CSDN博客
DBSCAN聚类算法——机器学习(理论+图解+python代码)_huacha__的博客-CSDN博客_dbscan聚类算法
Visualizing DBSCAN Clustering