人工智能——DBSCAN密度聚类（Python）
目录
1 概述
1.1 概念
1.2 DBSCAN数据点分类
2 DBSCAN算法流程
2.1 DBSCAN算法流程：
2.2 举例
3 案例1（Python实现 ）
3.1 案例
3.2 Python实现
3.3 结果
3.4 拓展
4 案例2（Python实现）
4.1 代码
4.2 结果
5 案例3（Python原码实现）
5.1 代码
5.2 结果
5.3 数据
6 参考
1 概述
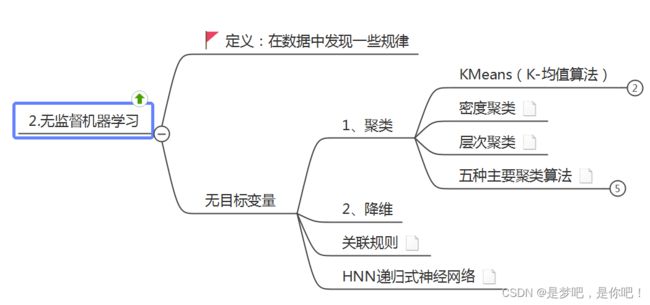
上一次讲解了人工智能——K-Means聚类算法（Python），这节课分享密度聚类：
1.1 概念
密度聚类，即基于密度的聚类(density-based clustering)，此类算法假设聚类结构能通过样本分布的紧密程度确定。前面所讲的都是把距离(欧式距离，闵科夫斯基距离，曼哈顿距离等)作为两个样本或者两个簇之间相似度的评价指标，因此导致了最终聚类结构大都是球状簇或者凸形集合，对任意形状的聚类簇比较吃力，同时对噪声数据不敏感，而基于密度的聚类算法可以发现任意形状的聚类，且对带有噪音点的数据起着重要的作用。
DBSCAN算法 是一种基于密度的聚类算法：• 聚类的时候不需要预先指定簇的个数• 最终的簇的个数不定1.2 DBSCAN数据点分类
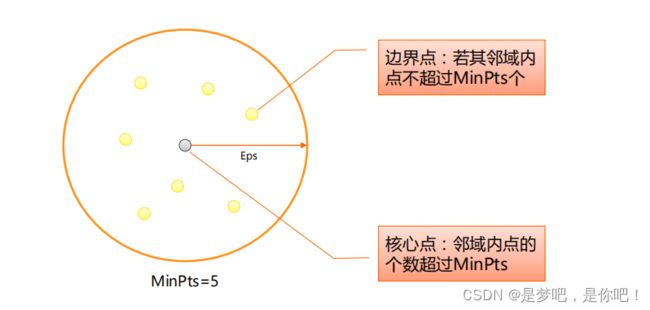
DBSCAN算法将数据点分为三类：• 核心点：在半径Eps内含有超过MinPts数目的点• 边界点：在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内• 噪音点：既不是核心点也不是边界点的点
2 DBSCAN算法流程
2.1 DBSCAN算法流程：
1.将所有点标记为核心点、边界点或噪声点；2.删除噪声点；3.为距离在Eps之内的所有核心点之间赋予一条边；4.每组连通的核心点形成一个簇；5.将每个边界点指派到一个与之关联的核心点的簇中（哪一个核心点的半径范围之内）。2.2 举例
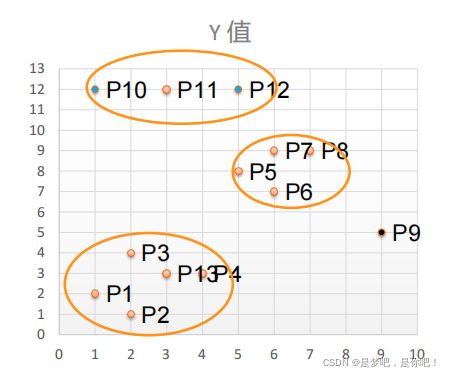
有如下13个样本点，使用DBSCAN进行聚类：
（1）取Eps=3，MinPts=3，依据DBSACN对所有点进行聚类（曼哈顿距离）。
（2）• 对每个点计算其邻域Eps=3内的点的集合。
• 集合内点的个数超过MinPts=3的点为核心点
• 查看剩余点是否在核心点的邻域内，若在，则为边界点，否则为噪声点。
（3）将距离不超过Eps=3的点相互连接，构成一个簇，核心点邻域内的点也会被加入到这个簇中。 则下侧形成3个簇。
3 案例1（Python实现 ）
3.1 案例
数据介绍：现有大学校园网的日志数据，290条大学生的校园网使用情况数据，数据包括用户ID，设备的MAC地址，IP地址，开始上网时间，停止上网时间，上网时长，校园网套餐等。利用已有数据，分析学生上网的模式。实验目的：通过DBSCAN聚类，分析学生 上网时间 和 上网时长 的模式。实验过程：• 使用算法： DBSCAN聚类算法• 实现过程：
数据实例：
3.2 Python实现
from sklearn.cluster import DBSCANDBSCAN主要参数 ：(1)eps: 两个样本被看作邻居节点的最大距离(2)min_samples: 簇的样本数(3)metric：距离计算方式例：sklearn.cluster.DBSCAN(eps=0.5, min_samples=5, metric='euclidean')
#*===================1. 建立工程，导入sklearn相关包===========================**
import numpy as np
import sklearn.cluster as skc
from sklearn import metrics
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
#*=================2. 读入数据并进行处理=====================================**
mac2id = dict() #mac2id是一个字典：key是mac地址value是对应mac地址的上网时长以及开始上网时间
onlinetimes = [] #value:对应mac地址的上网时长以及开始上网时间
f = open('TestData.txt', encoding='utf-8')
for line in f:
mac = line.split(',')[2] #读取每条数据中的mac地址
onlinetime = int(line.split(',')[6]) #上网时长
starttime = int(line.split(',')[4].split(' ')[1].split(':')[0]) #开始上网时间
if mac not in mac2id: #mac2id是一个字典：key是mac地址value是对应mac地址的上网时长以及开始上网时间
mac2id[mac] = len(onlinetimes)
onlinetimes.append((starttime, onlinetime))
else:
onlinetimes[mac2id[mac]] = [(starttime, onlinetime)]
real_X = np.array(onlinetimes).reshape((-1, 2))
X = real_X[:, 0:1]
#*==============3上网时间聚类，创建DBSCAN算法实例，并进行训练，获得标签=============**
db = skc.DBSCAN(eps=0.01, min_samples=20).fit(X) # 调 用 DBSCAN 方 法 进 行 训 练 ，labels为每个数据的簇标签
labels = db.labels_
#*=============4. 输出标签，查看结果===========================================**
print('Labels:') #打印数据被记上的标签，计算标签为-1，即噪声数据的比例。
print(labels)
raito = len(labels[labels[:] == -1]) / len(labels)
print('Noise raito:', format(raito, '.2%'))
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) #计算簇的个数并打印，评价聚类效果
print('Estimated number of clusters: %d' % n_clusters_)
print("Silhouette Coefficient: %0.3f" % metrics.silhouette_score(X, labels))
for i in range(n_clusters_): #打印各簇标号以及各簇内数据
print('Cluster ', i, ':')
print(list(X[labels == i].flatten()))
#*==========5.画直方图，分析实验结果========================================**
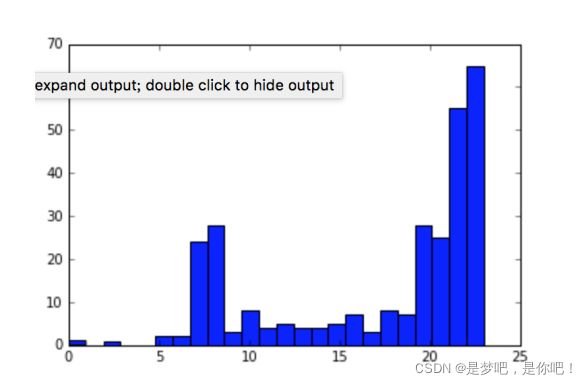
plt.hist(X, 24)
plt.show()
3.3 结果
转换直方图分析 观察：上网时间大多聚集在22：00和23：003.4 拓展
数据分布 vs 聚类：
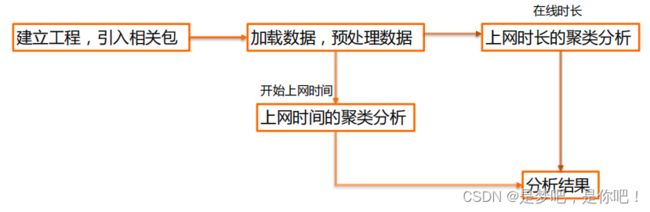
3-1. 上网时间聚类，创建DBSCAN算法实例，并进行训练，获得标签（上面已经分析过了）
3-2. 上网时长聚类，创建DBSCAN算法实例，并进行训练，获得标签：
结果：
Label表示样本的类别，-1表示DBSCAN划分为噪声。（1）按照上网时长DBSCAN聚了5类，右图所示，显示了每个聚类的样本数量、聚类的均值、标准差。（2）时长聚类效果不如时间的聚类效果明显。
4 案例2（Python实现）
4.1 代码
from sklearn.datasets import make_blobs:聚类数据生成器
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.cluster import DBSCAN
#matplotlib inline
X1, y1=datasets.make_circles(n_samples=5000, factor=.6,
noise=.05)
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]], cluster_std=[[.1]],
random_state=9)
X = np.concatenate((X1, X2)) #矩阵合并
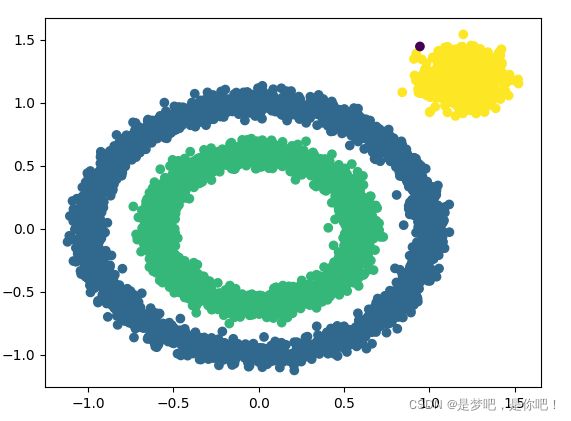
#展示样本数据分布
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
#eps和min_samples 需要进行调参
y_pred = DBSCAN(eps = 0.1, min_samples = 10).fit_predict(X)
#分类结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()4.2 结果
h2
5 案例3（Python原码实现）
5.1 代码
python中的zip()函数详解
python中的map函数
#*============================导入相关库=====================================**
import numpy as np
import numpy.random as random
from numpy.core.fromnumeric import * #查看矩阵或者数组的维数
import matplotlib.pyplot as plt
#*========================计算两个向量之间的欧式距离========================**
def calDist(X1 , X2 ):
sum = 0
for x1 , x2 in zip(X1 , X2): #转换成浮点型
sum += (x1 - x2) ** 2
return sum ** 0.5
#*==================获取一个点的ε-邻域（记录的是索引）=====================**
def getNeibor(data , dataSet , e):
res = []
for i in range(shape(dataSet)[0]):
if calDist(data , dataSet[i])=minPts:
coreObjs[i] = neibor
oldCoreObjs = coreObjs.copy()
k = 0#初始化聚类簇数
notAccess = list(range(n))#初始化未访问样本集合（索引）
while len(coreObjs)>0:
OldNotAccess = []
OldNotAccess.extend(notAccess)
cores = coreObjs.keys()
#随机选取一个核心对象
randNum = random.randint(0,len(cores))
cores=list(cores)
core = cores[randNum]
queue = []
queue.append(core)
notAccess.remove(core)
while len(queue)>0:
q = queue[0]
del queue[0]
if q in oldCoreObjs.keys() :
delte = [val for val in oldCoreObjs[q] if val in notAccess]#Δ = N(q)∩Γ
queue.extend(delte)#将Δ中的样本加入队列Q
notAccess = [val for val in notAccess if val not in delte]#Γ = Γ\Δ
k += 1
C[k] = [val for val in OldNotAccess if val not in notAccess]
for x in C[k]:
if x in coreObjs.keys():
del coreObjs[x]
return C
#*=====================预处理数据====================================**
def loadDataSet(filename):
dataSet = []
fr = open(filename)
for line in fr.readlines():
curLine = line.strip().split(',')
fltLine = map(float, curLine)
dataSet.append(list(fltLine))
return dataSet
def draw(C , dataSet):
color = ['r', 'y', 'g', 'b', 'c', 'k', 'm']
for i in C.keys():
X = []
Y = []
datas = C[i]
for j in range(len(datas)):
X.append(dataSet[datas[j]][0])
Y.append(dataSet[datas[j]][1])
plt.scatter(X, Y, marker='o', color=color[i % len(color)], label=i)
plt.legend(loc='upper right')
plt.show()
#*============================主函数===============================**
def main():
dataSet = loadDataSet("密度聚类.csv")
print(dataSet)
C = DBSCAN(dataSet, 0.11, 5)
draw(C, dataSet)
if __name__ == '__main__':
main()
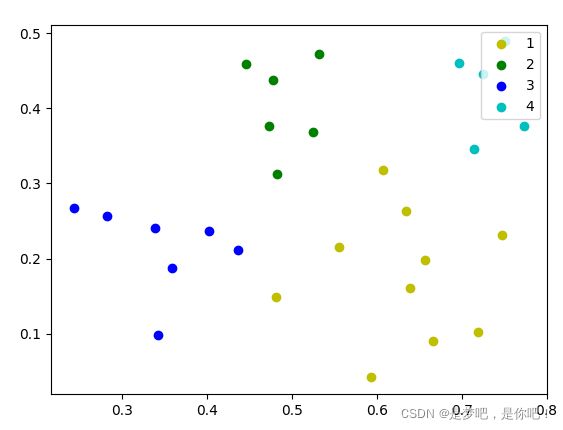
5.2 结果
5.3 数据
6 参考
————————————————
密度聚类之DBSCAN及Python实现