Yolov4详解
文章目录
- 前言
- 一、Yolov4网络结构
-
- 1.backbone:CSP Darknet-53
- 2.SPP池化
- 3.PAN和Yolo head
- 二、改进点
-
- 1.Mosaic数据增强
- 2.anchor偏移机制
- 3.正负样本匹配
- 4.Loss
前言
上一篇文章我们讨论了yolov3,yolov3在速度与精度上达到了一个较好的平衡,堪称经典之作,可惜在yolov3之后的原作者Joseph Redmon因为yolo的军事应用和对他人个人隐私风险而退出了yolo系列的研究,从此cv界痛失一员大将.但是经典之作总会源远流长,即使yolo原作者Joseph Redmon退出了研究,yolo算法巨大的影响力使得其他的研究者对yolo算法进行进一步讨论研究与发展,由此衍生出yolov3SPP,yolov4,yolov5等等一系列的算法,今天我们要讨论的是yolov4在yolov3的基础上做出的一些改动.v3
PS:如果是小白,建议看一看上一篇yolov3中的相关基础知识.
一、Yolov4网络结构
相对于yolov3,yolov4的改动还是比较多的,在网络结构方面主要的改动是修改了Backbone中的残差模块,在backbone后面又添加SPP模块,PAN与Yolo Head模块与yolov3基本一致,话不多说,直接上图.
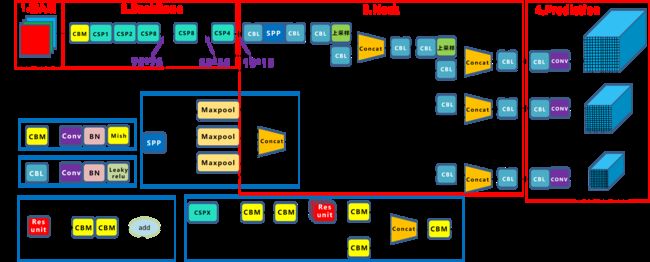
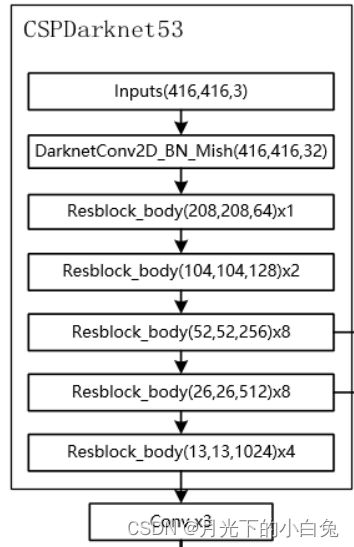
1.backbone:CSP Darknet-53
与Darknet53相比的第一点小改动,残差层之前的2层conv+bn+Relu变成了一层的conv+bn+Mish,主要原因是把Darknet53中残差层之上用来下采样的3x3卷积放入了Resblock_body中.
第二点则是对Residual_block的改进,Darknet53中的残差结构与resnet的结构基本相同,但在CSPDarknet53中提出了一种性能更好的残差结构,如下图所示:

对输入的feature map分别进行两次1x1卷积生成Part1与Part2,将Part1输入n个Residual结构中,最后将提取出的特征图与Part2在通道上拼接在一起,每经过一个Resblock_body通道数增加一倍,这种新的残差结构建立了一个大的残差边,这个大的残差边绕过了很多的残差结构,整个CSPDarknet的结构块,可看作一个大的残差块+内部多个小的残差块.
2.SPP池化
yolov4中新增了SPP池化,它借鉴了SPPnet的结构,但也不是完全相同.具体结构如下图
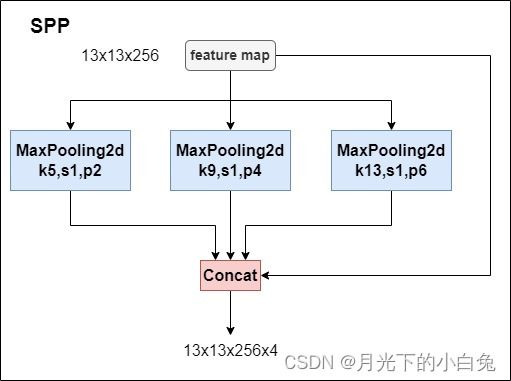
SPPnet主要解决的问题:
1.有效避免了R-CNN算法对图像区域剪裁、缩放操作导致的图像物体剪裁不全以及形状扭曲等问题
2.解决了卷积神经网络对图像重复特征提取的问题,大大提高了产生候选框的速度,且节省了计算成本。
而yolo中的SPP通过三个不同大小的MaxPooling层进行特征提取,获取到不同感受野大小的三个额外特征图,然后再将得到的特征图拼接在一起,这样使得经过SPP获取得到的特征图具有不同的感受野,特征图包含的信息更全面,另外一方面,Maxpooling层提取kernel_size大小的滑动窗口中最大的值,而上下文语义特征指的是多个相邻的像素点所组成的物体轮廓,个人认为,Maxpooling的滑动窗口提取相邻区域的最大值有一定的特征提取作用,因为都是邻近区域的最大值,所以可能在提取目标轮廓上有一定的促进作用,也就是说,SPP模块可能还增强特征图的上下文特征,但是Maxpooling层的局限性在于丢失大量信息,在使用pooling层还是conv层降图片尺度时我们需要考虑哪一种更适合自己的网络,但最近的很多网络都使用conv代替了pooling,如何减少信息丢失?这是一个值得思考的问题.
3.PAN和Yolo head
在PAN的论文中特征图融合用的是将两个特征图直接add的方法,但是yolov4中将之改为concat,为什么要改呢?
对于特征图融合的两种方法的理解:
add:将两个特征图直接相加,是resnet中的融合方法,基于这种残差堆叠相加,可以有效地减小因为网络层数加深而导致的cnn网络退化问题.add改变特征图像素值,并没有完全保留原本特征图信息,更多的可以看作对原特征图信息的一种补充,深层特征图在卷积过程中丢失了许多细节信息,通过add的方式得以补全,是在二维的平面上对特征图的增强.因此我认为add在进行图像特征增强时使用最佳.concat:将两个特征图在通道数方向叠加在一起,原特征图信息完全保留下来,再对原特征图增加一些我们认为是较好的特征图,丰富了特征图的多样性,是在空间上对原特征图的增强,这样在下一次卷积的过程中我们能得到更好的特征图.
Yolo head结构与yolov3中基本一致,此处不再多写.
二、改进点
1.Mosaic数据增强
从数据集中随机选取四张图片,进行随机裁剪,缩放,色域变换等等,最后将四张图拼接在一起

作者表示Mosaic数据增强的优点是丰富了检测物体的背景和小目标,并且在计算Batch Normalization的时候一次会计算四张图片的数据,使得mini-batch大小不需要很大,一个GPU就可以达到比较好的效果。
简而言之,当batch_size=1,正常我们只读取1张图片作为训练处理,而Mosaic将4张图片拼接起来使得网络同时处理四张图片,相当于将batch_size放大了4倍,因为图片输入的尺寸不能改变,所以原图片一般都是经过缩小再拼接的,这就导致原本可能大目标的物体变成中目标或者小目标,变相增加了网络训练过程中的小目标数量,因此在检测小目标精度将会得到提升.
2.anchor偏移机制
yolov3中对anchor中心点偏移量 ( t x , t y ) (t_x,t_y) (tx,ty)和先验框缩放量 ( t w , t h ) (t_w,t_h) (tw,th)进行了限制,使得anchor中心点的偏移量在 [ 0 , 1 ] [0,1] [0,1]之间,这样大大减少了anchor中心点偏移过远导致召回率和精度过低.
yolov4中考虑了sigmoid函数的局限性,并对anchor中心点偏移量 ( t x , t y ) (t_x,t_y) (tx,ty)的进一步限制,下图所示
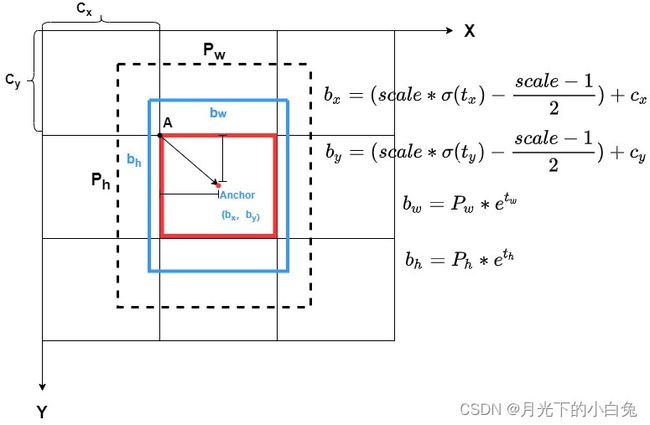
( c x , c y c_x,c_y cx,cy) 网格左上角坐标
( P w , P h P_w,P_h Pw,Ph) 先验框宽与高
( b x , b y b_x,b_y bx,by) Anchor最终坐标
( b w , b y b_w,b_y bw,by) 最终预测框宽与高
由上图可知,yolov4在处理anchor的偏移量( t x , t y t_x,t_y tx,ty)的公式于yolov3不大一样,因为sigmoid函数在x趋近于 + ∞ +∞ +∞与 − ∞ -∞ −∞的时候才能无限接近于1,这就导致某些中心点在网格顶点的目标无法较好的被预测到,因此我们想到添加一个除了 σ ( x ) \sigma(x) σ(x)之外的限制参数 s c a l e scale scale,使得偏移量的值域增大到1以上,从而使得某些中心点在网格顶点的目标也能得到较好得回归效果.在我们平时搭建网络过程中, s c a l e scale scale一般取为2的时候效果较好.所以公式可以简化为:
b x = ( 2 ∗ σ ( t x ) − 0.5 ) + c x b_x =(2*\sigma(t_x)-{0.5})+c_x bx=(2∗σ(tx)−0.5)+cx b y = ( 2 ∗ σ ( t y ) − 0.5 ) + c y b_y =(2*\sigma(t_y)-{0.5})+c_y by=(2∗σ(ty)−0.5)+cy
b w = P w ∗ e t w b_w=P_w*e^{t_w} bw=Pw∗etw b h = P h ∗ e t h b_h=P_h*e^{t_h} bh=Ph∗eth
3.正负样本匹配
针对yolov3的匹配机制导致正样本过少,正负样本匹配不均匀的问题,在匹配正样本的过程之中,在正样本匹配机制上做了以下两点改进:
1. 不再限制一个GT只匹配一个最大iou的anchor template,设定一个阈值,只要anchor template的iou大于这个阈值则判定为正样本
2.( t x , t y t_x,t_y tx,ty)的值域从[0,1]扩展到了[-0.5,1.5],首先我们计算出GT框的中心点坐标并找到该中心点坐标落 入的网格位置,因此在yolov4中一个GT框可用多个anchor去匹配。
如果GT框中心点落入到网格左上方,相对于左边网格左顶点和上方网格的左顶点而言,该中心点的偏移量在[-0.5,1.5]的范围之内,所以左方和上方的网格皆可为该GT框提供anchor template进行正样本匹配,这样就增加了更多正样本.
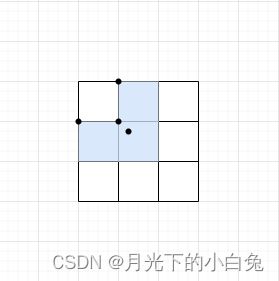
同理可知:
如果GT框中心点落入右上,则右方和上方的网格的anchor template也可作正样本匹配,
如果GT框中心点落入左下,则左方和下方的网格的anchor template也可作正样本匹配,
如果GT框中心点落入右下,则右方和下方的网格的anchor template也可作正样本匹配,
还有一种极端情况就是GT中心点正好落入该网格中心点,这时就只需要用这一个网格的anchor template匹配正样本就足够了.
通过这两种方式大大的增加了正样本数量,一定程度上缓解了正负样本匹配不均匀问题.
4.Loss
在学习Loss之前yolov4中还有一个值得说一说的改进点为label smoothing标签平滑 ,给自己数据集打过标签的同学都知道,手动打标签也会存在一定的误差,而在训练过程中我们将标签值设为1,也是会存在一定的误差的,因此我们对标签值设立一个很小很小的惩罚项 ϵ \epsilon ϵ,在一定程度上可以平衡手动标签的损失.
yolov4的损失函数改动主要是在定位损失上面,在yolov3的文章中我们已经提到过了 L o s s l o c Loss_{loc} Lossloc采用MSE损失函数计算不太合理了,因为一个好的损失函数应该既考虑到预测框与Gt框的宽高损失与中心点损失,还要考虑到iou重合度,个人认为两个框之间的重合度更能反应真实框与预测框之间的差异.
所以yolov4中采用了CIOU来计算定位损失,
L o s s l o c = ∑ i ∈ p o s ( 1 − c i o u ) Loss_{loc}=\sum_{i\in pos}(1-ciou) Lossloc=i∈pos∑(1−ciou)
C I O U = I O U − ( G T 框 与 预 测 框 中 心 点 的 欧 式 距 离 同 时 包 含 预 测 框 和 真 实 框 的 最 小 闭 包 区 域 的 对 角 线 距 离 ) − α v CIOU=IOU-( \frac{GT框与预测框中心点的欧式距离}{同时包含预测框和真实框的最小闭包区域的对角线距离})-αv CIOU=IOU−(同时包含预测框和真实框的最小闭包区域的对角线距离GT框与预测框中心点的欧式距离)−αv
α = v 1 − I O U + v α =\frac{v}{1-IOU+v} α=1−IOU+vv
v = 4 π 2 ∗ ( a r c t a n w g t h g t − a r c t a n w h ) 2 v = \frac{4}{\pi ^2}*(arctan\frac{w_{gt}}{h_{gt}}-arctan\frac{w}{h})^2 v=π24∗(arctanhgtwgt−arctanhw)2