wikioi 1034 家 实时动态的网络流量(费用流)
因为随着时间的推移。网络侧变得,因此,常见的网络流量也解决不了这个问题,。如果T毕竟运输时间。
为此。我们可以基于时间分割点,所有的点将被分割为T点。
对于每一个点,下一次甚至一个容量为本人INF边缘,费用1边缘。这意味着目前的空间站等待1。
每一个点对于下一个时刻能到的点。连一条边,容量是这艘太空船的容量,费用是1。
源点连0时刻的地球,容量为k,全部的月球连接汇点。费用都为0。
每次找到一条最短路进行增广。若增广流量达到总人数,则退出。
这时候找到最后到达月球的时刻,就是终于时刻。
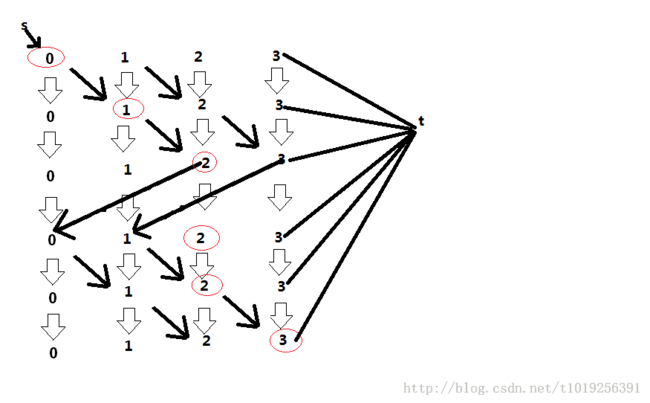
建图的样子。
#include<cstdio>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
#define MAXN 10000
#define MAXM 1000000
#define INF 0x3f3f3f3f
struct node
{
int u,v,f,c,next;
}e[MAXM];
int n,head[MAXN],pre[MAXN],dist[MAXN],vis[MAXN],ans;
int en,s,t,maxflow,mincost; //s源点。t汇点
void add(int u,int v,int c,int f)//加边
{
e[en].u=u;
e[en].v=v;
e[en].c=c;
e[en].f=f;
e[en].next=head[u];
head[u]=en++;
e[en].u=v;
e[en].v=u;
e[en].c=-c;
e[en].f=0;
e[en].next=head[v];
head[v]=en++;
}
int spfa()
{
int i,u,v;
for(i=0;i<=t;i++)
pre[i]=-1,vis[i]=0,dist[i]=INF;
dist[s]=0;
vis[s]=1;
queue<int>q;
q.push(s);
while(!q.empty())
{
u=q.front();
q.pop();
for(i=head[u];i!=-1;i=e[i].next)
{
v=e[i].v;
if(e[i].f>0&&dist[u]+e[i].c<dist[v])
{
dist[v]=dist[u]+e[i].c;
pre[v]=i;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
vis[u]=0;
}
if(dist[t]==INF)
return 0;
return 1;
}
void add()
{
int v;
int maxf=INF;
for(v=pre[t];~v;v=pre[e[v].u])
maxf=min(maxf,e[v].f);
for(v=pre[t];~v;v=pre[e[v].u])
{
e[v].f-=maxf;
e[v^1].f+=maxf;
}
ans=max(ans,e[pre[t]].u);//保存最后到达月球的时刻,越后面下标越大。
maxflow+=maxf;
}
void init()
{
maxflow=0;
mincost=0;
en=0;
memset(head,-1,sizeof(head));
}
int num[55][55],have[55],r[55];
int main()
{
int i,j,a,b,c,m,k;
while(scanf("%d%d%d",&n,&m,&k)!=EOF)
{
ans=0;
init();
for(int i=1;i<=m;i++)
{
scanf("%d%d",&r[i],&have[i]);
for(int j=0;j<have[i];j++)
{
scanf("%d",&num[i][j]);
if(num[i][j]==-1) num[i][j]=n+1;
}
}
int T=100;
s=(n+2)*(T+1);
t=s+1;
add(s,0,0,k);
for(int i=0;i<=T;i++)
{
if(i!=T) for(int j=0;j<=n+1;j++) add(j*(T+1)+i,j*(T+1)+i+1,1,INF); //在此空间站停留到下一时刻
if(i==0) continue;
for(int x=1;x<=m;x++)
{
int times=i%have[x];
int from,to;
if(times==0) from=num[x][have[x]-1],to=num[x][times];
else from=num[x][times-1],to=num[x][times];
add(from*(T+1)+i-1,to*(T+1)+i,1,r[x]); //i时刻从from到to空间站
}
}
for(int i=(n+1)*(T+1);i<=(n+1)*(T+1)+T;i++) add(i,t,0,INF);
while(spfa())
add();
if(maxflow==k) printf("%d\n",ans%(T+1));
else puts("0");
}
return 0;
}
版权声明:本文博客原创文章,博客,未经同意,不得转载。