图像算法六 —— K-Means和KNN

6. K-Means和KNN

K-Means和KNN的区别和联系

区别：

• K-Means是无监督学习的聚类算法，没有样本输入；KNN是有监督学习的分类算法，有对应的类别输出。
• KNN基本不需要训练，对测试集里的点只需要找到在训练集中最接近的$k$个点，用这最近的$k$个点的类别来决定测试点的类别；K-Means则有明显的训练过程，找到$k$个类别的最佳质心，从而决定样本簇类别。

联系：

• 两个算法都包含一个过程，即找出和某一点最近的点
• 两者都利用了最近邻的思想

K-Means聚类算法

简介

​ K-Means算法是无监督的聚类算法，它实现起来比较简单，聚类效果也不错，因此应用广泛。K-Means算法有大量的变体优化，如初始优化K-Means++、距离计算优化elkan K-Means算法和大数据情况下的优化Mini Batch K-Means算法等。

​ K-Means最常用的就是基于欧氏距离的聚类算法，其认为两个目标的距离越近，相似度越大。

算法原理

K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本划分为$K$个簇，让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。

如果用数据表达式来表示，假设簇划分为$(C_1,C_2,\cdots ,C_k)$，则我们的目标是最小化平方误差E：

$$E=\sum _{i=1}^k\sum _{x\in C_i}||x-{\mu }_i|{|}_2^2$$

其中，

${\mu }_i$——簇$C_i$的均值向量，也被称为质心，表达式为：

$${\mu }_i=\frac{1}{|C_i|}\sum _{x\in C_i}x$$

如果之间求上式的最小值并不容易，这是一个NP难的问题，因此只能采用启发式的迭代方法。

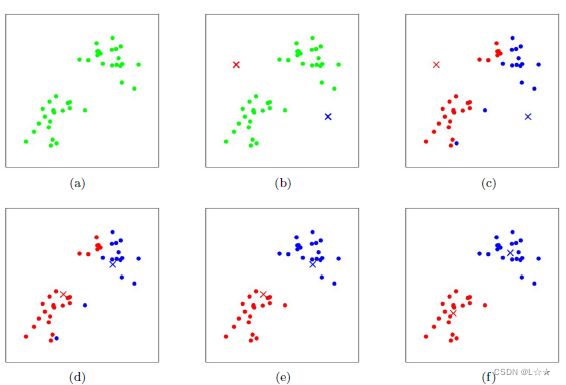
K-Means采用的启发式方法很简单，如下图所示：

图（a） ——初始数据，假设$k=2$

图（b） ——随机选择两个$k$类对应的类别质心，即图中的红色和蓝色质心，然后分别求样本中所有点到这两个质心的距离，并标记每个样本的类别和该样本距离最小的质心的类别，如图（c）。

经过计算样本和红色质心与蓝色质心的距离，我们得到了所有样本第一轮迭代后的类别，此时我们对当前标记为红色和蓝色的点，分别求其质心，如图（d） 所示，新的红色质心和蓝色质心的位置已经发生了变动。

图（e） 和 图（f） 重复了 图（c） 和 图（d） 的过程，即将所有点的类别标记为距离最近的质心，并求新的质心。

最终我们得到的两个类别如图（f）。

算法步骤

K-Means算法步骤为：

• （1）选择初始化的$k$个样本作为初始聚类中心$a=a_1,a_2,\cdots ,a_k$
• （2）针对数据集中每个样本$x_i$计算它到$k$个聚类中心的距离，并将其分到距离最小的聚类中心所对应的类中；
• （3）针对每个类别$a_j$，重新计算它的聚类中心$a_j=\frac{1}{|c_i|}{\sum }_{x\in c_i}x$（即，属于该类的所有样本的质心）
• 重复上述（2）、（3）操作，直到达到某个终止条件（迭代次数，最小误差变化等）

伪代码及复杂度

伪代码：

获取数据 n 个 m 维的数据
随机生成 K 个 m 维的点
while(t)
    for(int i=0;i < n;i++)
        for(int j=0;j < k;j++)
            计算点 i 到类 j 的距离
    for(int i=0;i < k;i++)
        1. 找出所有属于自己这一类的所有数据点
        2. 把自己的坐标修改为这些数据点的中心点坐标
end

复杂度：

时间复杂度：$O(tknm)$。其中，

​ $t$——迭代次数

​ $k$——簇的数目

​ $n$——样本点数

​ $m$——样本点维度

空间复杂度：$O(m(n+k))$。其中，

​ $k$——簇的数目

​ $m$——样本点维度

​ $n$——样本点数

优缺点

优点：

• 容易理解，聚类效果不错，虽然是局部最优，但是往往局部最优已经可以满足要求。
• 在处理大数据集时，该算法可以保证较好的延伸性
• 当簇近似高斯分布时，效果非常好。
• 算法复杂度低
• 算法可解释性强
• 主要调参的参数仅仅是簇数$k$

缺点：

• $k$值需要人为设定，不同$k$值得到的结果不同。
• 对于初始的簇中心敏感，不同选取方式会得到不同的结果。
• 对异常值敏感。
• 样本只能归为一类，不适合多分类任务。
• 不适合太离散的分类，样本类别不均衡的分类、非凸形状的分类。

K-Means初始化优化——K-Means++

由于$k$个初始化的质心位置选择，对最后的聚类结果和运行时间都有很大的影响，因此需要选择合适的$k$个质心。

如果仅仅是完全随机的选择，有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法进行优化。

K-Means++对于初始化质心的优化策略也很简单，如下：

• （1）从输入的数据点集合中，随机选择一个点作为第一个聚类中心${\mu }_1$
• （2）对于数据中的每一个点$x_i$，计算它与已选择的聚类中心的距离$D(x_i)=argmin||x_i-{\mu }_r|{|}^{2}r=1,2,\cdots ,k_{selected}$
• （3）选择一个新的数据点作为新的聚类中心，选择原则是：$D(x)$较大的点，被选取作为聚类中心点的概率较大。
• （4）重复（2）和（3）直到选择出$k$个聚类质心
• （5）利用这$k$个质心来作为初始化质心去运行标准的K-Means算法。

K-Means距离计算优化—— elkan K-Means

​ 在传统的K-Means算法中，我们在每轮迭代时，要计算所有样本点到所有质心的距离，这样会比较耗时。因此elkan K-Means算法就是从这部分入手改进，它的目标是减少不必要的距离计算。

​ elkan K-Means利用了两边之和大于第三边，以及两边之差小于第三边的三角形性质，来减少距离的计算。

• 第一种规律：是对于一个样本点$x$和两个质心${\mu }_{j_1}$、${\mu }_{j_2}$。我们预先计算出了这两个质心之间的距离$D(j_1,j_2)$，则如果计算发现$2D(x,j_1)\le D(j_1,j_2)$，我们立刻就知道$D(x,j_1)\le D(x,j_2)$。此时我们不需要再计算$D(x,j_2)$，也就是省了一步距离计算。

• 第二种规律：是对于一个样本点$x$和两个质心${\mu }_{j_1}$、${\mu }_{j_2}$。我们可以得到$D(x,j_2)\ge \max \{0,D(x,j_1)-D(j_1,j_2)\}$。从三角形的性质，也很容易得到。

  利用上述两个规律，elkan K-Means比起传统的K-Means迭代速度有很大的提高。但是如果我们的样本特征是稀疏的，有缺失值的话，这个方法就不起作用了，此时某些距离无法计算，则不能使用该算法。

K-Means大样本优化——Mini Batch K-Means

在传统的K-Means算法中，要计算所有的样本点到所有质心的距离。如果样本量非常大，比如达到10万以上，特征有100以上，此时用传统的算法非常耗时，就算加上elkan K-Means优化也依旧如此。在大数据时代，这样的场景越来越多，此时Mini Batch K-Means也应运而生。

顾名思义，Mini Batch，也就是用样本集中的一部分样本来做传统的K-Means，这样就可以避免样本量太大时的计算难题，算法收敛速度也大大加快。然而，此时的代价就是我们的聚类精度会有一些下降。一般来说，这个降低的幅度在可以接受的范围内。

在Mini Batch K-Means中，我们会选择一个合适的批样本大小batch size，我们仅仅用batch size个样本来做K-Means聚类，这个batch size一般是通过无放回的随机采样得到的。

为了增加算法的准确性，我们一般会跑多几次Mini Batch K-Means算法，用得到不同的随机采样集来得到聚类簇，选择其中最优的聚类簇。

KNN 算法（K近邻算法）

简介

k近邻算法（k-nearest neighbor，KNN）是一种基本分类和回归方法，是有监督学习方法里的一种常用方法。

K近邻算法，即是给定一个训练数据集，其中的实例类别已经确定。分类时，对于，根据其k个最近邻的训练实例类别，通过多数表决等方式进行预测。

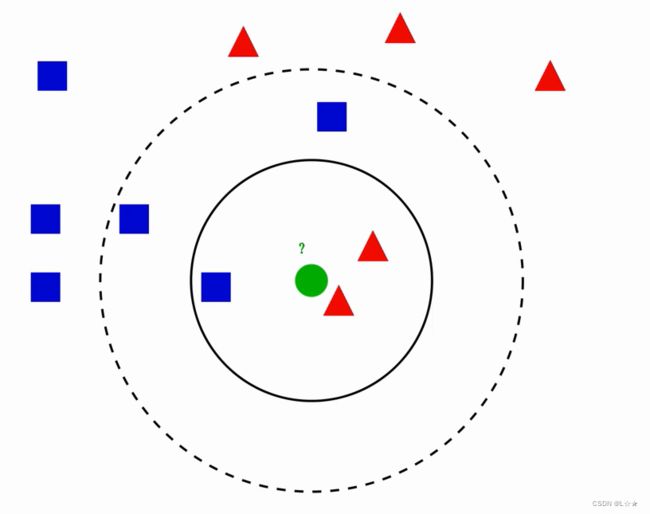
k近邻算法用一句通俗的古语来说就是：“物以类聚，人以群分”。你要看一个实例的类别，你就可以看它附近是什么类别。如下图1.1所示，当要判断绿色实例的类别的时候，我们可以看看它的附近有哪些类，然后采取多数表决的决策规则（红色2个多于蓝色1个），于是把绿色实例也分类为红色那一类。

KNN三要素

简述

$k$近邻法三要素：

• 距离度量——常用的距离度量是欧氏距离及更一般的pL距离。
• $k$值的选择——$k$值小时，$k$近邻模型更复杂，容易发生过拟合；$k$值大时，$k$近邻模型更简单，又容易欠拟合。因此$k$值得选择会对分类结果产生重大影响。$k$值的选择反映了对近似误差与估计误差之间的权衡，通常由交叉验证选择最优的$k$。
• 分类决策规则——分类决策规则往往是多数表决，即由输入实例的$k$个邻近输入实例中的多数类决定输入实例的类。

距离度量

设特种空间$x$是$n$维实数向量空间，$x_i,x_j\in \chi$，$x_i={\left(x_i^{(1)},x_i^{(2)},\cdots ,x_i^{(n)}\right)}^T$ ，$x_j={\left(x_j^{(1)},x_j^{(2)},\cdots ,x_j^{(n)}\right)}^T$，则：$x_i$， $x_j$的$L_p$距离定义为：

$$L_p(x_i,x_j)={\left(\sum _{i=1}^n|x_i^{(i)}-x_j^{(l)}{|}^p\right)}^{\frac{1}{p}}$$

• $p=1$——曼哈顿距离
• $p=2$——欧氏距离
• $p=\infty$——切比雪夫距离

一般采用二维欧氏距离

交叉验证选$k$值

在许多实际应用中，数据是不重组的。因此为了选择好的模型，可以采用交叉验证的方法。

交叉验证的基本思想是：重复地使用数据，把给定的数据进行切分，将切分的数据组合为训练集和测试集，在此基础上反复进行训练测试以及模型的选择。

在实现过程中，通常采用sklearn.model_selection.cross_val_score()实现交叉验证选取$k$值。

分类决策规则

knn使用的分类决策规则是多数表决。

如果损失函数为0-1损失函数，那么要使误分类率最小 即 使经验风险最小，多数表决规则实际上就等同于经验风险最小化。

KNN实现

实现K近邻算法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索。k近邻法最简单的实现方法是线性扫描，也就是暴力法计算输入实例到每一个训练实例的距离，然后取前k个距离最短的采取多数表决规则进行分类。但是如果训练集的数据量很大时，这种方法就不可行了。为了提高k近邻的搜索效率，可以考虑使用特殊的结构存储训练数据，以减少距离计算的次数，常用的有kd（kd tree）树方法。

sklearn封装KNN方法解析：

sklearn.neighbors.KNeighborsClassifier(n_neighbors = 5,
                       weights='uniform',
                       algorithm = '',
                       leaf_size = '30',
                       p = 2,
                       metric = 'minkowski',
                       metric_params = None,
                       n_jobs = None
                       )

参数如下：

参数如下：

n_neighbors：这个值就是指 KNN 中的 “K”了。前面说到过，通过调整 K 值，算法会有不同的效果。
weights（权重）：最普遍的 KNN 算法无论距离如何，权重都一样，但有时候我们想搞点特殊化，比如距离更近的点让它更加重要。这时候就需要 weight 这个参数了，这个参数有三个可选参数的值，决定了如何分配权重。参数选项如下：
• ‘uniform’：不管远近权重都一样，就是最普通的 KNN 算法的形式。
• ‘distance’：权重和距离成反比，距离预测目标越近具有越高的权重。
• 自定义函数：自定义一个函数，根据输入的坐标值返回对应的权重，达到自定义权重的目的。
algorithm：在 sklearn 中，要构建 KNN 模型有三种构建方式，1. 暴力法，就是直接计算距离存储比较的那种放松。2. 使用 kd 树构建 KNN 模型 3. 使用球树构建。 其中暴力法适合数据较小的方式，否则效率会比较低。如果数据量比较大一般会选择用 KD 树构建 KNN 模型，而当 KD 树也比较慢的时候，则可以试试球树来构建 KNN。参数选项如下：
• ‘brute’ ：蛮力实现
• ‘kd_tree’：KD 树实现 KNN
• ‘ball_tree’：球树实现 KNN
• ‘auto’： 默认参数，自动选择合适的方法构建模型
不过当数据较小或比较稀疏时，无论选择哪个最后都会使用 ‘brute’
leaf_size：如果是选择蛮力实现，那么这个值是可以忽略的，当使用KD树或球树，它就是是停止建子树的叶子节点数量的阈值。默认30，但如果数据量增多这个参数需要增大，否则速度过慢不说，还容易过拟合。
p：和metric结合使用的，当metric参数是"minkowski"的时候，p=1为曼哈顿距离， p=2为欧式距离。默认为p=2。
metric：指定距离度量方法，一般都是使用欧式距离。
• ‘euclidean’ ：欧式距离
• ‘manhattan’：曼哈顿距离
• ‘chebyshev’：切比雪夫距离
• ‘minkowski’： 闵可夫斯基距离，默认参数
n_jobs：指定多少个CPU进行运算，默认是-1，也就是全部都算。

属性如下：

classes_ : 分类器已知的类别标签，返回ndarray标签数组。
effective_metric_ ：距离度量，和上述参数中metric参数设定的距离度量一致。
effective_metric_params_：指标函数附加的关键字参数，对于大多数距离指标，将会和metric参数相同，但如果effective_metric_params_属性设置为‘minkowski’，那么也可能包含p参数的值。返回的形式是字典。
outputs_2d_：训练时当y的形状为（n，）或（n，1），则返回False，否则返回True。

方法如下：

fit(X, y)：使用X作为训练数据，y作为标签目标数据进行数据拟合训练。
get_params([deep])：获取参数组成的字典。
kneighbors([X, n_neighbors, return_distance])：找寻一个点的k个邻居。
predict(X)：根据提供的数据去预测它的类别标签。
predict_proba(X)：返回测试数据X的概率估计值。
score(X, y[, sample_weight])：返回给定数据和标签的平均准确度。
set_params(params)：设置估值器的参数。

KNN算法优缺点

优点：

• 简单易用，相比于其他算法，KNN算是比较简洁明了的算法。即使没有很高的数学基础，也可以搞懂它的原理
• 模型训练时间快
• 预测效果好
• 对异常值不敏感

缺点：

• 对内存要求较高，因为该方法存储了所有训练数据
• 预测阶段可能很慢
• 对不相关的功能和数据规模敏感