Silverlight实用窍门系列:54.详解Silverlight中的矩阵变换MatrixTransform,实现其余各种变换【附带实例源码】
在Silverlight中的MatrixTransform矩阵变换相对上篇文章所述的变换较复杂一些,但这种变换也更灵活。
MatrixTransform的实质:让需要变换的元素上的每一个像素点*矩阵得到这个点的新坐标。
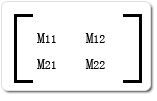
下面我们来看看MatrixTransform的3*3矩阵元素图如下:
其中的数字0、0、1在Silverlight中是固定不变的,所以我们可以不加理会,而M11,M12,M21,M22是我们需要相乘的坐标矩阵模块。如下图所示:
那么我们看看一个老坐标(X,Y)*矩阵的核心算法如下图所示,得到新坐标点(X1,Y1):
但是这个新坐标点并非就是最终点位,还有元素OffsetX、OffsetY为偏移坐标量(X1+OffsetX,Y1+OffsetY)这个点位才是最终的坐标点如下图所示:
总结得出原图像上每一个坐标点位的点经过以下算法之后才是其最终坐标点位:X2=X*M11+Y*M21+OffsetX , Y2=X*M12+Y*M22+OffsetY.
最后我们来看看在源码中的用法是: <MatrixTransform Matrix="M11 M12 M21 M22 OffsetX OffsetY"></MatrixTransform>
下面我们来看一个实例,通过MatrixTransform实现上篇文章所述的几种变换。
MatrixTransform实现RotateTransform效果
<!--按照(0,0)为中心点90度变换-->
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="48,49,0,0" Name="image11"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_001.png" Opacity=".3" />
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="48,49,0,0" Name="image1"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_001.png" >
<Image.RenderTransform>
<!--m11(0) m12(1) m21(-1) m22(0) OffsetX(0) OffsetY(0)-->
<!--0*X+ -1*X=-1X 1*Y+0*Y =1Y -1X+0 1Y+0 =>新坐标点(-1X,1Y) -->
<MatrixTransform Matrix="0 1 -1 0 0 0"></MatrixTransform>
</Image.RenderTransform>
</Image>
MatrixTransform实现ScaleTransform效果
<!--0.6倍缩放变换-->
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="139,49,0,0" Name="image21"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_002.png" Opacity=".3"/>
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="139,49,0,0" Name="image2"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_002.png">
<Image.RenderTransform>
<!--m11(0.6) m12(0) m21(0) m22(0.6) OffsetX(0) OffsetY(0)-->
<!--0.6*X+0*X=0.6X 0*Y+0.6*Y =0.6Y 0.6X+0 0.6Y+0 =>新坐标点(0.6X,0.6Y) -->
<MatrixTransform Matrix="0.6 0 0 0.6 0 0"></MatrixTransform>
</Image.RenderTransform>
</Image>
MatrixTransform实现SkewTransform效果
<!--倾斜变换-->
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="226,49,0,0" Name="image31"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_003.png" Opacity=".3"/>
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="226,49,0,0" Name="image3"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_003.png" >
<Image.RenderTransform>
<!--m11(1) m12(0) m21(1) m22(1) OffsetX(0) OffsetY(0)-->
<!--1*X+1*X=2X 0*Y+1*Y =1Y 2X+0 1Y+0 => 新坐标点(2X,0Y) -->
<MatrixTransform Matrix="1 0 1 1 0 0"></MatrixTransform>
</Image.RenderTransform>
</Image>
MatrixTransform实现TranslateTransform效果
<!--TranslateTransform变换-->
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="331,49,0,0" Name="image41"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_004.png" Opacity=".3"/>
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="331,49,0,0" Name="image4"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_004.png" >
<Image.RenderTransform>
<!--m11(1) m12(0) m21(0) m22(1) OffsetX(10) OffsetY(50)-->
<!--1*X+0*X=2X 0*Y+1*Y =0Y 1X+10 1Y+50 => 新坐标点(1X+10,1Y+50) -->
<MatrixTransform Matrix="1 0 0 1 10 50"></MatrixTransform>
</Image.RenderTransform>
</Image>
MatrixTransform实现TransformGroup效果
<!--以Y轴翻转-->
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="426,49,0,0" Name="image51"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_005.png" Opacity=".3"/>
<Image Height="50" HorizontalAlignment="Left" VerticalAlignment="Top" Margin="426,49,0,0" Name="image5"
Stretch="Fill" Width="50" Source="/SLTrans;component/iPhone_005.png" >
<Image.RenderTransform>
<!--m11(1) m12(0) m21(0) m22(-1) OffsetX(0) OffsetY(100)-->
<!--1*X+ 0*X=1X 0*Y+ -1*Y =-1Y 1X+0 -1Y+100 => 新坐标点(1X,-1Y) -->
<MatrixTransform Matrix="1 0 0 -1 0 0"></MatrixTransform>
</Image.RenderTransform>
</Image>
最后我们来看实例的运行效果如下,如需源码请点击SLMatrixTransform.rar下载。