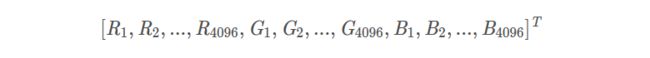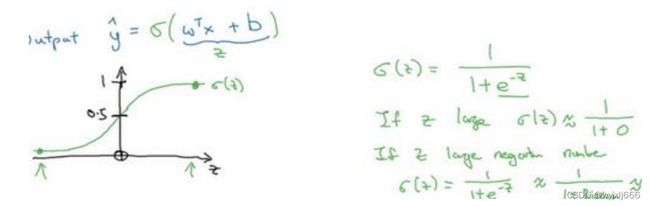深度学习基础----吴恩达课后编程练习（一）识别猫

目录

前言

一、数据预处理

1.加载数据

 2.数据降维处理

          3.标准化处理

二、搭建神经网络

1.定义模型结构

2.初始化模型参数

3.循环迭代

     3.1 计算当前的损失（正向传播）

     3.2 计算当前的梯度（反向传播）

     3.3 迭代更新参数（梯度下降）

4.数据预测与封装

4.1 数据预测

4.2 数据封装

5.实验结果测试

5.1 实验结果

5.2 学习率的选择

5.3 测试

总结

---

---

---

前言

前两周学习了吴恩达的机器学习课程的前两章部分，并配合黄海广的学习笔记，懵懵懂懂的开始了深度学习之旅........学习完第二周课程后，我又参照大佬的博客在pycharm做了课程一的实验：具有神经网络思维的逻辑回归

在这个实验中要使用逻辑回归搭建一个简单的单层神经网络，实现经典的猫图的识别实验了。

  简单来说该实验核心思想是： 逻辑回归是一个用于二分类的算法。假如你有一张图片作为输入，比如这只猫，如果识别 这张图片为猫，则输出标签 1 作为结果；如果识别出不是猫，那么输出标签 0 作为结果。

为了进一步加深记忆，写个博客记录一下

一、数据预处理

1.加载数据

首先肯定是要导入各种数据库了，Numpy是Python中科学计算的基础包，方面后续各种运算，和向量化处理。pyplot画图用的，h5py应该是用于读取图片数据集中的数据的，lr_utils建立是用于存放数据的

​
#导入数据库
import numpy as np
import matplotlib.pyplot as plt
import h5py
from lr_utils import load_dataset
import numpy as np
from PIL import Image
import imageio
from skimage.transform import resize

 顺便看看这些输入图片数据的存储结构 

train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = load_dataset()
m_train = train_set_y.shape[1] #训练集里图片的数量。
m_test = test_set_y.shape[1] #测试集里图片的数量。
num_px = train_set_x_orig.shape[1] #训练、测试集里面的图片的宽度和高度（均为64x64）像素。
#现在看一看我们加载的东西的具体情况
print ("训练集的数量: m_train = " + str(m_train))
print ("测试集的数量 : m_test = " + str(m_test))
print ("每张图片的宽/高 : num_px = " + str(num_px))
print ("每张图片的大小 : (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("训练集_图片的维数 : " + str(train_set_x_orig.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集_图片的维数: " + str(test_set_x_orig.shape))
print ("测试集_标签的维数: " + str(test_set_y.shape))

结果如下： 

可以看到训练集train是209张，测试集是50张，像素是 64×64，3代表RGB三种颜色

再看一下一张图片数据里的照片

index=25
plt.imshow(train_set_x_orig[index])   #pyplot 中用于显示图像的方法imshow
plt.show()

 

 2.数据降维处理

   转化测试集x和训练集X矩阵为（n*m），对于单个训练样本而言，所有的输入按照列矩阵的形式传入网络，即输入 x的是 nx×1 维的矩阵，但是一幅 64×64 图像的在数据集中是以 64×64×3 的矩阵形状进行存储的，为了满足神经网络的输入格式，在 Python 中可以使用 reshape 函数改变矩阵的形状，对于一个形状为 (a,b,c,d) 的矩阵 M1而言，通过M1.reshape(M1.shape[0],−1).T 就可以将其转换为形状为 (b×c×d,a)的矩阵了。
   其中第一项参数 M1.shape[0]表示的就是 M1​ 原来的第一维长度 a，第二项参数 −1表示将后面的所有维度堆叠成一个维度，这样就得到了一个形为 (a,b×c×d)的矩阵，再通过".T"进行转置，就得到了 a个列矩阵堆叠得到的“向量化矩阵”。这里的解释参考了：B站吴恩达深度学习视频笔记（1-14）——实战3：识别猫图

#X_flatten = X.reshape(X.shape [0]，-1).T ＃X.T是X的转置
#将训练集的维度降低并转置。
train_set_x_flatten  = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
#将测试集的维度降低并转置。
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
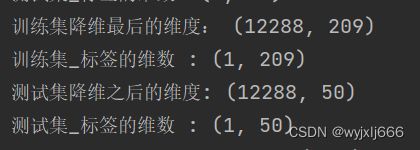
print ("训练集降维最后的维度： " + str(train_set_x_flatten.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集降维之后的维度: " + str(test_set_x_flatten.shape))
print ("测试集_标签的维数 : " + str(test_set_y.shape))

使用这个方法就可以对数据集中的图像数据进行降维处理了
结果如下：

按列看，每一列代表一个样本图像的所有 RGB 数值，共有209个训练样本，因此train_set_x_flatten 有209列。数字 12288 是 RGB 全部铺平的数值总量
因为图片是 64×64 的，因此 R、G、B各有 64×64=4096个值，RGB 共三层4096×3=12288

 

3.标准化处理

  标准化处理是为了加速训练神经网络，机器学习中一个常见的预处理步骤是对数据集进行居中和标准化，这意味着可以减去每个示例中整个numpy数组的平均值，然后将每个示例除以整个numpy数组的标准偏差。但对于图片数据集，它更简单，更方便，几乎可以将数据集的每一行除以255（像素通道的最大值），因为在RGB中不存在比255大的数据，所以我们可以放心的除以255，让标准化的数据位于[0,1]之间，现在标准化我们的数据集：

train_set_x = train_set_x_flatten / 255
test_set_x = test_set_x_flatten / 255

二、搭建神经网络

1.定义模型结构

这个神经网络模型只有一个输入层和一个输入层，没有隐藏层

逻辑回归的公式定义如下：

 定义一个sigmoid激活函数即上图的函数

"""激活函数"""
def sigmoid(z):
    """
    参数：
        z  - 任何大小的标量或numpy数组。

    返回：
        s  -  sigmoid（z）
    """
    s = 1 / (1 + np.exp(-z))
    return s

函数图形： 

2.初始化模型参数

代码如下

#初始化参数w和b”“”
def initialize_with_zeros(dim):
    """
         此函数为w创建一个维度为（dim，1）的0向量，并将b初始化为0。

         参数：
             dim  - 我们想要的w矢量的大小（或者这种情况下的参数数量）

         返回：
             w  - 维度为（dim，1）的初始化向量。
             b  - 初始化的标量（对应于偏差）
     """

    w = np.zeros(shape = (dim,1))
    b = 0
    # 使用断言来保证我要的数据是正确的，如果不完全确定一个向量的维度，用断言语句
    assert(w.shape == (dim, 1))
    assert(isinstance(b, float) or isinstance(b, int))  # b的类型是float或者是int
    return (w, b)

3.循环迭代

循环迭代就是通过训练代价函数来得到最佳的参数w和b

     3.1 计算当前的损失（正向传播）

    #正向传播
    A = sigmoid(np.dot(w.T,X)+b)#计算激活值，向量化
    cost = (-1/m)*np.sum(Y*np.log(A)+(1-Y)*np.log(1-A))

     3.2 计算当前的梯度（反向传播）

    #反向传播
    dw=(1/m)*np.dot(X,(A-Y).T)
    db=(1/m)*np.sum(A-Y)

整体propagate函数：

def propagate(w,b,X,Y):
    """
    实现前向和后向传播的成本函数及其梯度。
    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 矩阵类型为（num_px * num_px * 3，训练数量）
        Y  - 真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据数量)

    返回：
        cost- 逻辑回归的负对数似然成本
        dw  - 相对于w的损失梯度，因此与w相同的形状
        db  - 相对于b的损失梯度，因此与b的形状相同
    """

    m=X.shape[1]
    #正向传播
    A = sigmoid(np.dot(w.T,X)+b)#计算激活值，向量化
    cost = (-1/m)*np.sum(Y*np.log(A)+(1-Y)*np.log(1-A))

    #反向传播
    dw=(1/m)*np.dot(X,(A-Y).T)
    db=(1/m)*np.sum(A-Y)
    ##使用断言确保我的数据是正确的
    assert(dw.shape == w.shape)
    assert(db.dtype == float)
    cost=np.squeeze(cost)
    assert(cost.shape == ())
    #创建一个字典，把dw和db保存起来

    grads={
        "dw":dw,
        "db":db
    }
    return(grads,cost)

     3.3 迭代更新参数（梯度下降）

     目标是通过最小化成本函数 J 来学习 w和b 。 我们需要写下两个步骤并遍历它们：
        1）计算当前参数的成本和梯度，使用propagate（）。
        2）使用w和b的梯度下降法则更新参数。

def optimize(w,b,X,Y,num_iterations,learning_rate,print_cost=False):
    """
    此函数通过运行梯度下降算法来优化w和b

    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 维度为（num_px * num_px * 3，训练数据的数量）的数组。
        Y  - 真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据的数量)
        num_iterations  - 优化循环的迭代次数
        learning_rate  - 梯度下降更新规则的学习率
        print_cost  - 每100步打印一次损失值

    返回：
        params  - 包含权重w和偏差b的字典
        grads  - 包含权重和偏差相对于成本函数的梯度的字典
        成本 - 优化期间计算的所有成本列表，将用于绘制学习曲线。

    提示：
    我们需要写下两个步骤并遍历它们：
        1）计算当前参数的成本和梯度，使用propagate（）。
        2）使用w和b的梯度下降法则更新参数。
    """
    costs=[]
    for i in range(num_iterations):
       grads,cost=propagate(w,b,X,Y)
       dw=grads["dw"]
       db=grads["db"]
       w = w-learning_rate * dw
       b=b-learning_rate*db
       #记录成本
       if i % 100 == 0:
           costs.append(cost)
           #打印成本数据

       if(print_cost)and(i%100==0):
           print("迭代的次数: %i ， 误差值： %f" % (i,cost))
    params = {
                "w" : w,
                "b" : b }
    grads = {
            "dw": dw,
            "db": db }
    return (params , grads , costs)

这里的for循环不能避免

4.数据预测与封装

4.1 数据预测

ef predict(w,b,X):
    """
        使用学习逻辑回归参数logistic （w，b）预测标签是0还是1，

        参数：
            w  - 权重，大小不等的数组（num_px * num_px * 3，1）
            b  - 偏差，一个标量
            X  - 维度为（num_px * num_px * 3，训练数据的数量）的数据

        返回：
            Y_prediction  - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组（向量）

        """
    m=X.shape[1] #图片的数量
    Y_prediction=np.zeros((1,m))
    w=w.reshape(X.shape[0],1)

    #计算预测猫在图片中出现的概率
    A=sigmoid(np.dot(w.T,X)+b)
    for i in range(A.shape[1]):
        Y_prediction[0,i]=1 if A[0,i]>0.5 else 0
    #使用断言
    assert(Y_prediction.shape==(1,m))
    return Y_prediction

如果不确定一个向量的维度，用断言语句可以避免不必要的bug。另外，为了确保矩阵或向量所需要的维数时，要多使用reshape操作。

4.2 数据封装

在前面我们已经将模型的主体即向前传播向后传播和梯度下降都模块化地完成了，接下来把这些步骤拼接在一起得到最终的模型

ef model(X_train,Y_train,X_test,Y_test,num_iterations=2000,learning_rate=0.5,print_cost=False):
    """
        通过调用之前实现的函数来构建逻辑回归模型

        参数：
            X_train  - numpy的数组,维度为（num_px * num_px * 3，m_train）的训练集
            Y_train  - numpy的数组,维度为（1，m_train）（矢量）的训练标签集
            X_test   - numpy的数组,维度为（num_px * num_px * 3，m_test）的测试集
            Y_test   - numpy的数组,维度为（1，m_test）的（向量）的测试标签集
            num_iterations  - 表示用于优化参数的迭代次数的超参数
            learning_rate  - 表示optimize（）更新规则中使用的学习速率的超参数
            print_cost  - 设置为true以每100次迭代打印成本

        返回：
            d  - 包含有关模型信息的字典。
        """
    w,b=initialize_with_zeros(X_train.shape[0])
    parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
    # 从字典“参数”中检索参数w和b
    w, b = parameters["w"], parameters["b"]
    #预测测试/测试集的例子
    Y_prediction_test=predict(w , b, X_test)
    Y_prediction_train = predict(w, b, X_train)
    # 打印训练后的准确性
    print("训练集准确性：", format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100), "%")
    print("测试集准确性：", format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100), "%")

    d = {
        "costs": costs,
        "Y_prediction_test": Y_prediction_test,
        "Y_prediciton_train": Y_prediction_train,
        "w": w,
        "b": b,
        "learning_rate": learning_rate,
        "num_iterations": num_iterations}
    return d

5.实验结果测试

5.1 实验结果

print("====================测试model====================")
#这里加载的是真实的数据，请参见上面的代码部分。
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)

结果：

 

绘制图：

#绘制图
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()

结果：

 

 可以看到成本在下降，表明参数正在被学习

5.2 学习率的选择

研究学习率的可能选择。为了让渐变下降起作用，（学习率代表迭代下降的幅度）我们必须明智地选择学习速率。学习率α  决定了我们更新参数的速度。如果学习率过高，我们可能会“超过”最优值。同样，如果它太小，我们将需要太多迭代才能收敛到最佳值。这就是为什么使用良好调整的学习率至关重要的原因。

learning_rates = [0.01, 0.001,0.005, 0.0001]
models = {}
for i in learning_rates:
    print ("learning rate is: " + str(i))
    models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
    print ('\n' + "-------------------------------------------------------" + '\n')

for i in learning_rates:
    plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))

plt.ylabel('cost')
plt.xlabel('iterations')

legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
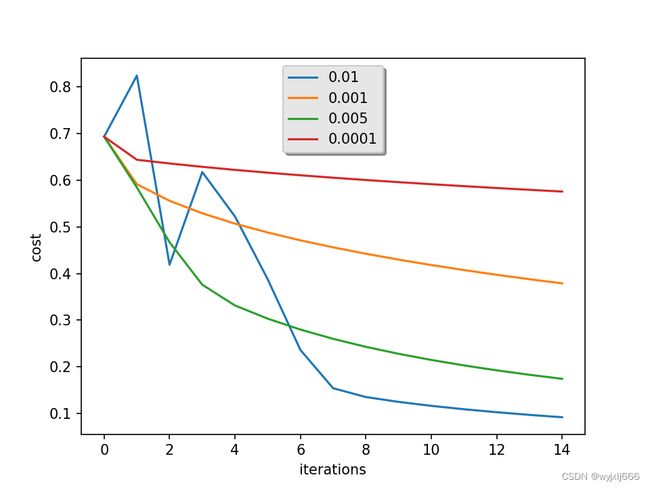
plt.show()

结果：

learning rate is: 0.01
训练集准确性： 99.52153110047847 %
测试集准确性： 68.0 %

-------------------------------------------------------

learning rate is: 0.001
训练集准确性： 88.99521531100478 %
测试集准确性： 64.0 %

-------------------------------------------------------

learning rate is: 0.0001
训练集准确性： 68.42105263157895 %
测试集准确性： 36.0 %

-------------------------------------------------------

 

 

可以看到当学习率为0.01时cost下降最快 ，训练集的准确性最高，在iteations值在[0-4]时，=0.01时cost函数有震荡，应该就是在这个范围内学习率过高，可能“超过了”最优值。

5.3 测试

用自己的图片测试一下模型

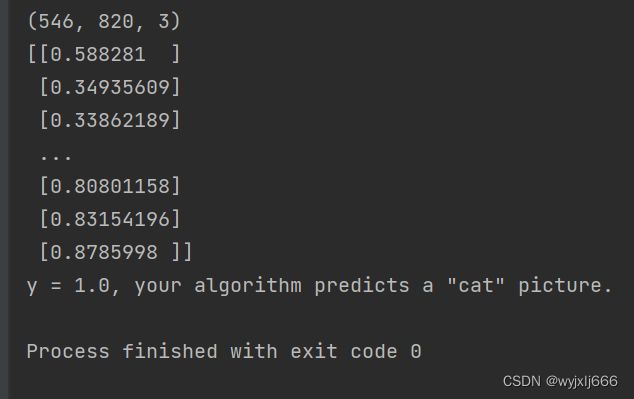
用自己的照片测试模型
my_image = "456.jpg"   # 修改你图像的名字
## END CODE HERE ##
# We preprocess the image to fit your algorithm.
fname = "images/" + my_image                       # 图片位置
image = np.array(imageio.imread(fname))            # 读入图片为矩阵
print(image.shape)

# print(num_px)
# 先把图片放缩到 64x64
# 转置图片为 (num_px*num_px*3, 1)向量
my_image = resize(image, output_shape=(num_px, num_px)).reshape((1, num_px * num_px * 3)).T
print(my_image)
my_predicted_image = predict(d["w"], d["b"], my_image)  # 用训练好的参数来预测图像
plt.imshow(image)
# print(classes)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") +  "\" picture.")

图片：（来自网络）                                    结果：

 

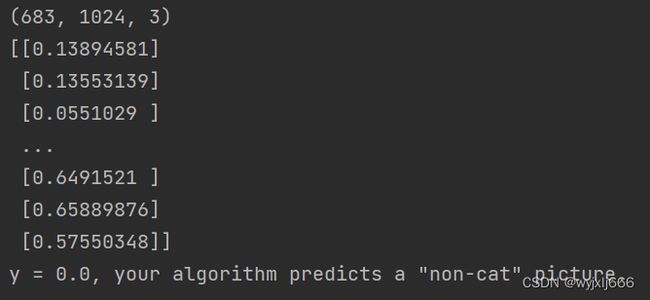
再来一张：                                               结果：

  

额，这张没识别出来。。。。。 总的来说，这个模型的训练集准确性最高有99%，而测试集最高才70%，因此只能说是这个模型的问题，具体以后怎么优化，继续努力学习吧！

总结

学习神经网络第一课还算愉快，（虽然历时半个月，中间自己一遍一遍的推导思考才勉强理解）不足之处是：不会python语言，自己完全是比照着大佬们写好的完整代码敲的，要补充对python的学习了。