“山大地纬杯”第十二届山东省ICPC大学生程序设计竞赛 回顾

A Seventeen

大意：
给出一个数字 n 用 1 - n 所有的数字 和 加减乘操作 获得 17
思路：
n<=3 无法构造
这时我们可以发现一个性质：相邻的四个数字 a a+1 a+2 a+3 (a-(a+1)-(a+2)+(a+3)=0
因此只要构造好 4 5 6 7 四种情况 ，其他的情况往后加四个数字即可
例如 8 就是 4 往后加四个数字，加完大小不变

#include
using namespace std;
       
#define fi first
#define se second  
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef unsigned long long ull;
typedef long long ll;
const int N = 5e5+10;
const int NN = 1e5+100;
const int p = 998244353;
typedef pair<int,int>PII;
const int inf = 2147483647;

int n;

int main(){
	cin>>n;
	
	if(n<4){
		cout<<"-1";
	}else{
		int cnt=0;
		if(n%4==0){
			cout<<"(2+4)*3-1";
			for(int i=5;i<=n;i++){
				if(cnt==0||cnt==3) cout<<"+";
				else cout<<"-";
				cout<<i;
				cnt=(cnt+1)%4;
			}
		}else if(n%4==1){
			cout<<"2*4+1+3+5";
			for(int i=6;i<=n;i++){
				if(cnt==0||cnt==3) cout<<"+";
				else cout<<"-";
				cout<<i;
				cnt=(cnt+1)%4;
			}
		}else if(n%4==2){
			cout<<"4*6-1-5-3+2";
			for(int i=7;i<=n;i++){
				if(cnt==0||cnt==3) cout<<"+";
				else cout<<"-";
				cout<<i;
				cnt=(cnt+1)%4;
			}
		}else{
			cout<<"4*7-5-6+3-1-2";
			for(int i=8;i<=n;i++){
				if(cnt==0||cnt==3) cout<<"+";
				else cout<<"-";
				cout<<i;
				cnt=(cnt+1)%4;
			}
		}
	}
}

E Subsegments

问题简述：

给出一个序列
求有多少个区间的区间乘积 同余x

思路：维护前缀积,线性复杂度优化

对于式子 si / sj = x

对于每个前缀积
1.我们可以把它当成 si ，都换成 si , sj = si / x 去找前面 si * inv(x) 的数量 每次维护 si 初始化时 mp[1]=1
2.我们可以把它当成 sj , 都换成 sj , si = sj * x 去找前面 sj 的数量 每次维护 sj * x 初始化时 mp[x]=1

当 x = 0 时，特殊处理
例如
6 0
1 2 0 3 0 1
要计算贡献用到双指针， l ，r
每个 0 对于答案的贡献是 (i-l)*(n-r+1) r=i
代表从 这个 0 左侧选一个数作左区间 ，在右侧选一个数作右区间，计算完贡献
左指针右移到 r ，避免重复计算(相当于把已经计算的区间截掉了)
当 x ！= 0 时
线性处理 ， 当遇到 t = 0 时 ， 那么前缀区间必然乘积不可能为 x ，截掉前面序列，即清空前边序列，重新初始化

#include
using namespace std;
       
#define fi first
#define se second  
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef unsigned long long ull;
typedef long long ll;
const int N = 5e5+10;
const int NN = 1e5+100;
const int p = 998244353;
typedef pair<int,int>PII;
const int inf = 2147483647;

ll n,x;

ll t,ans,k=1;
unordered_map<ll,int>mp;

ll qp(ll a,ll b){
	ll res=1;
	
	while(b){
		if(b%2!=0) res=res*a%p;
		b/=2;
		a=a*a%p;
	}
	return res;
}


int main()
{
	cin>>n>>x;
	
	int l=0;
	
	if(x==0){
		for(int i=1;i<=n;i++){
			scanf("%lld",&t);
			if(t==0){
				ans+=(i-l)*(n-i+1);
				l=i;
			}
		}
	}else{
		mp[x]=k=1;
		for(int i=1;i<=n;i++){
			scanf("%lld",&t);
			if(t==0){
				mp.clear();
				mp[x]=k=1;
			}else{
				k=1ll*k*t%p;
				ans+=mp[k];
				mp[1ll*k*x%p]++;
			}
		}
	}
	
	cout<<ans;
	
	
}

//int main()
//{
//	cin>>n>>x;
//	
//	int l=0;
//	
//	if(x==0){
//		for(int i=1;i<=n;i++){
//			scanf("%lld",&t);
//			if(t==0){
//				ans+=(i-l)*(n-i+1);
//				l=i;
//			}
//		}
//	}else{
//		mp[1]=k=1;
//		for(int i=1;i<=n;i++){
//			scanf("%lld",&t);
//			if(t==0){
//				mp.clear();
//				mp[1]=k=1;
//			}else{
//				k=1ll*k*t%p;
//				ans+=mp[k*qp(x,p-2)%p];
//				mp[k]++;
//			}
//		}
//	}
//	
//	cout<
//}

H Counting

直接模拟即可

#include
using namespace std;
       
#define fi first
#define se second  
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef unsigned long long ull;
typedef long long ll;
const int N = 1e5+10;
const int NN = 1e5+100;
const int p = 998244353;
typedef pair<int,int>PII;
const int inf = 2147483647;

int n,m,k,t;

int b[2001][2001];
struct node{
	int x,y;
}a[2001];
int ans;
string s[2001];


int main(){
	
	IOS;
	
	cin>>n>>m>>k>>t;
	
	for(int i=1;i<=k;i++){
		cin>>a[i].x>>a[i].y;
		ans+=b[a[i].x][a[i].y];
		b[a[i].x][a[i].y]++;
	}
	
	for(int i=1;i<=k;i++){
		b[a[i].x][a[i].y]--;
	}
	
	cout<<ans<<"\n";
	
	for(int i=1;i<=k;i++) cin>>s[i];
	for(int i=0;i<t;i++){
		ans=0;
		for(int j=1;j<=k;j++){
			if(s[j][i]=='U'){
				a[j].x--;
			}else if(s[j][i]=='D'){
				a[j].x++;
			}else if(s[j][i]=='L'){
				a[j].y--;
			}else{
				a[j].y++;
			}
			ans+=b[a[j].x][a[j].y];
			b[a[j].x][a[j].y]++;
		}
		cout<<ans<<"\n";
		for(int i=1;i<=k;i++){
			b[a[i].x][a[i].y]--;
		}
	}
	
}

J Football Match

/*
大意：
给出一个红旗
会进行 放缩 和 旋转两个操作
给出 A B 两个点
求剩余 12 个点的坐标

思路：
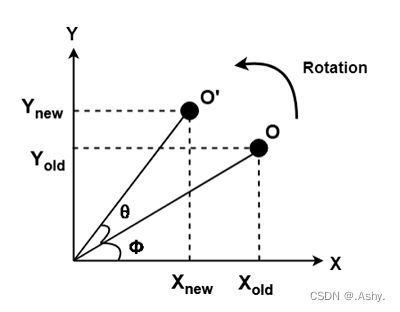
旋转一定会有 旋转角 和 基点 ，根据基点求出其他点未旋转之前的偏移量，然后根据旋转角旋转各点 即可，
一定注意旋转角的处理

	ox   = r cosB, oy = r sinB
    ox'  = r cos ( A + B)
        = r ( cosA cosB – sinA sinB ) 
        = r cosB cosA – r sinB sinA 
        = x cosA – y sinA
    oy'  = r sin ( A + B ) 
        = r ( sinA cosB + cosA sinB )  
        = r cosB sinA + r sinB cosA 
        = x sinA + y cosA

		注意正方向，以逆时针为正

*/

要注意 三角函数里面计算的都是弧度值

#include
using namespace std;
       
#define fi first
#define se second  
#define pi acos(-1) 
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef unsigned long long ull;
typedef long long ll;
const int N = 5e5+10;
const int NN = 1e5+100;
const int p = 998244353;
typedef pair<int,int>PII;
const int inf = 2147483647;

int t;
double xa,ya,xb,yb,xc,yc,xd,yd,xe,ye,xf,yf,xg,yg,xh,yh,xi,yi,xj,yj,xk,yk,xl,yl,xm,ym,xn,ynn;
double theta;

void pp(double &x,double &y){
	double t1=x,t2=y;
	x=xa+cos(theta)*t1-sin(theta)*t2;
	y=ya+sin(theta)*t1+cos(theta)*t2;
}

int main(){
	cin>>t;
	
	while(t--){
		cin>>xa>>ya>>xb>>yb;
		double d=sqrt((xa-xb)*(xa-xb)+(ya-yb)*(ya-yb));
		double w=d*1.5;
		double R=d/20.0*6.0;
		double r=R/sin(pi/2-pi/5)*sin(pi/10);
		
		xc=w;                          yc=d;
		xd=w;                          yd=0;
		xe=w/2.0;                      ye=d/2.0+R;
		xf=w/2.0+r*sin(pi/5);          yf=d/2.0+r*cos(pi/5);
		xn=w/2.0-r*sin(pi/5);          ynn=d/2.0+r*cos(pi/5);
		xg=w/2.0+R*cos(pi/10);         yg=d/2.0+R*sin(pi/10);
		xm=w/2.0-R*cos(pi/10);         ym=d/2.0+R*sin(pi/10);
		xl=w/2.0-r*cos(pi/10);         yl=d/2.0-r*sin(pi/10);
		xh=w/2.0+r*cos(pi/10); 		   yh=d/2.0-r*sin(pi/10);
		xj=w/2.0;                      yj=d/2.0-r;
		xk=w/2.0-R*sin(pi/5);     	   yk=d/2.0-R*cos(pi/5);
		xi=w/2.0+R*sin(pi/5);          yi=d/2.0-R*cos(pi/5);
		
		theta=acos((yb-ya)/d);
		if(xb>xa) theta=2*pi-theta;
		//theta = - theta
        //注意这里的角度，如果xb>xa则计算的角要取负值
        
        pp(xc,yc);pp(xd,yd);
        pp(xe,ye);pp(xf,yf);
        pp(xg,yg);pp(xh,yh);
        pp(xi,yi);pp(xj,yj);
        pp(xk,yk);pp(xl,yl);
        pp(xm,ym);pp(xn,ynn);
		
		
		printf("%.8lf %.8lf\n",xc,yc);
		printf("%.8lf %.8lf\n",xd,yd);
		printf("%.8lf %.8lf\n",xe,ye);
		printf("%.8lf %.8lf\n",xf,yf);
		printf("%.8lf %.8lf\n",xg,yg);
		printf("%.8lf %.8lf\n",xh,yh);
		
		printf("%.8lf %.8lf\n",xi,yi);
		printf("%.8lf %.8lf\n",xj,yj);
		printf("%.8lf %.8lf\n",xk,yk);
		printf("%.8lf %.8lf\n",xl,yl);
		printf("%.8lf %.8lf\n",xm,ym);
		printf("%.8lf %.8lf\n",xn,ynn);
	}
}
/*
1
1 0 0 20
1
0 0 1 20
*/

K Coins

完全背包问题，但范围很大
先试着枚举一定数量的硬币，发现超过一定范围后，答案都是A
所以前面的枚举，后边的直接输出 A

#include
using namespace std;
       
#define fi first
#define se second  
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef unsigned long long ull;
typedef long long ll;
const int N = 1e5+10;
const int NN = 1e5+100;
const int p = 998244353;
typedef pair<int,int>PII;
const int inf = 2147483647;

int dp1[N],dp2[N];
int a[5]={0,2,3,17,19};
int b[5]={0,5,7,11,13};

int t;

int main(){
	for(int i=1;i<=100000;i++){
		dp1[i]=1e9+10;
		dp2[i]=1e9+10;
	}
	
	dp1[0]=1;dp1[2]=1;dp1[3]=1;dp1[17]=1;dp1[19]=1;
	dp2[0]=1;dp2[5]=1;dp2[7]=1;dp2[11]=1;dp2[13]=1;
	
	
	for(int i=1;i<=4;i++){
		for(int j=a[i];j<=100000;j++){
			dp1[j]=min(dp1[j],dp1[j-a[i]]+1);
		}
	}
	
	
	for(int i=1;i<=4;i++){
		for(int j=b[i];j<=100000;j++){
			dp2[j]=min(dp2[j],dp2[j-b[i]]+1);
		}
	}
	
	cin>>t;
	
	while(t--){
		int i;
		cin>>i;
		if(i<=100000){
			if(dp1[i]==1e9+10&&dp2[i]==1e9+10){
				cout<<"-1\n";
			}else if(dp1[i]==1e9+10){
				cout<<"B\n";
			}else if(dp2[i]==1e9+10){
				cout<<"A\n";
			}else{
				if(dp1[i]<dp2[i]){
					cout<<"A\n";
				}else if(dp1[i]>dp2[i]){
					cout<<"B\n";
				}else{
					cout<<"both\n";
				}
			}
		}else{
			cout<<"A\n";
		}
	}
}