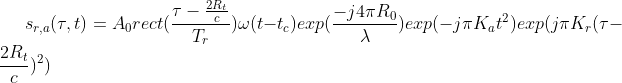【3】合成孔径雷达（SAR）的二维回波信号与距离多普勒（RD）算法 （附matlab代码）

合成孔径雷达发射信号以线性调频信号（LFM）为基础，目前大部分合成孔径雷达都是LFM体制，为了减轻雷达重量也采用线性调频连续波（FMCW）体制；为了获得大带宽亦采用线性调频步进频（FMSF）体制。

（1）LFM信号

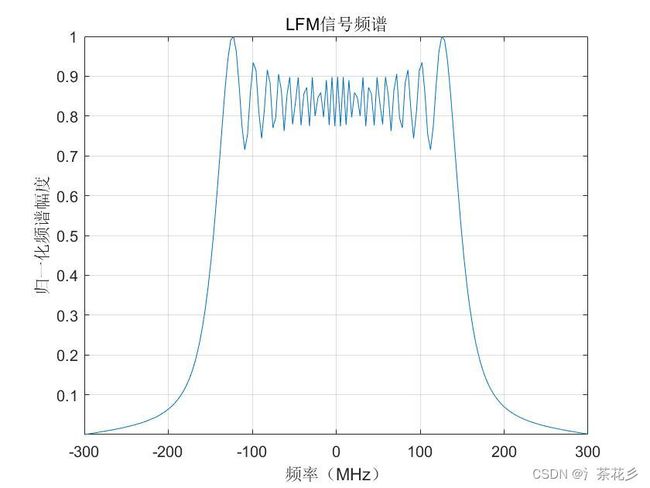
LFM的主要特点在于可以使载波的瞬时频率随调制信号的变化而变化，当其频率线性增加时，称为正调频；当其频率线性减少时，称为负调频。LFM信号的幅度频谱存在部分起伏现象，这是由菲涅尔积分造成的；信号的频谱并不完全限制在-B/2~B/2之内，随着时宽带宽积的增大，信号的幅频特性越接近矩形，顶部起伏也会减小。LFM解决了探测距离和分辨率之间的矛盾，在雷达和制导武器上得到广泛应用。LFM的时域表示为：

其中，T为时宽，K为调频率，rect为矩形窗。

求LFM信号的频谱需要对其作FFT，得到：

存在指数二次项积分，需采用驻定相位原理（POSP）求解，驻定相位点为：

因此求得频谱为

LFM的时域图和频谱图如下（附matlab代码）。

 

 %%%%%%%%% 线性调频信号LFM%%%%%%%%
%% LFM时域波形
clc; clear; close all;
f0 = 0;    %雷达中心频率
T = 3e-7;  %脉宽
B = 3e8;    %带宽
fs = 2*B; %采样率
Ts = 1/fs; %采样时间
N = T/Ts; %采样数
k = B/T;   %调频率
t = linspace(-T/2,T/2,N);%时间
y = exp(1j*(2*pi*f0*t + pi*k*t.^2));%LFM信号
figure;
plot(t*1e6,real(y));xlabel('时间（us）');ylabel('幅度');
title('LFM信号时域波形（实部）');
figure;
plot(t*1e6,imag(y));xlabel('时间（us）');ylabel('幅度');
title('LFM信号时域波形（虚部）');
grid on; axis tight;
%% LFM频谱图
S = fftshift(fft(y));     %频谱
f = linspace(-fs/2,fs/2,N);%频率轴
figure;
plot(f*1e-6,abs(S)./max(max(abs(S))));
xlabel('频率（MHz）')
ylabel('归一化频谱幅度');
title('LFM信号频谱');

 （2）快时间与慢时间

在合成孔径雷达成像中，快时间和慢时间是一个相对的概念。在工程上，快时间指的是脉内时间变化，慢时间是脉间时间变化。

雷达发射信号是以脉冲的形式发射的，发射频率称为脉冲重复频率（PRF），PRF的设定是根据雷达的功能和性能确定的。从几K到几十K，甚至几百K。一般星载SAR的PRF为几K，每一个脉冲都有一个时间戳，这个连续的时间戳合起来叫做慢时间。如下图t1到t6为慢时间标记。

 雷达发射脉冲信号的周期为T，T=1/PRF。雷达有效信号能量时间占一个雷达信号周期的比例称为占空比，也就是说发射的有效信号不总是充满整个雷达信号周期。周期内的有效能量部分的时间称为快时间，一般用来表示。

这种慢时间和快时间在主观上是交替进行的，慢时间沿方位向播放，快时间沿距离向播放，这就形成了SAR的“停-走-停”成像模式。

（3）SAR的二维回波信号

在低轨星载和机载SAR使用中，回波是以“停-走-停”的方式录取的，它是以快时间轴和慢时间轴构成的二维平面。如下图所示。

 合成孔径雷达一般发射的是LFM信号,快时间的数学表达式为

fc为载频，Kr为调频率，rect（.）为脉冲包络。假设，一个散射系数为A0的点目标在雷达发射波束内，距离雷达的距离为R，则雷达接受到的回波是发射信号与目标散射系数的卷积，因此接收信号为(忽略后向散射引起的相位变化):

上式看起来是一个距离向一维回波，但是它的慢时间包含在R中。由于录取平台是运动的，因此R会随着平台位置的变化而改变，如下图所示。

 慢时间在t1-t11时刻距离目标的R1-R11一直发生变化。R关于慢时间的表达式为(正侧式SAR为例)：

R0为雷达到目标的最短参考距离。将R(t)带入回波中，得到SAR的二维回波信号：

为方位信号包络。对Rt进行泰勒展开取近似得到

带入到二维回波信号中，整理得到：

其中，Ka为方位向多普勒调频率：

由回波信号可以看到，在方位向和距离向分别存在两个线性调频信号。

（4）正侧视距离多普勒（RD）算法

一个简单的距离多普勒算法包括距离压缩、距离徙动矫正、方位压缩。其中距离压缩和方位压缩通过LFM匹配滤波或去斜处理实现。距离徙动矫正是补偿掉不同方位位置回波引起的Rt的变化，若距离徙动远小于距离分辨率，则不需要进行距离徙动矫正，RD成像仅剩下距离压缩和方位压缩，且这两步操作没有先后之分。

把二维回波信号分解，仅考虑相位项，距离向的对应LFM信号为

方位向的对应LFM信号为

因此，RD算法的算法流程如下图所示：

 算法中的距离参考信号为

其中为距离包络，为距离向参考时间（快时间）。

方位参考信号为

经过距离压缩和方位压缩，得到简单RD算法的成像效果。5个点目标未进行RCM的matlab代码如下：

%% RD算法   含距离徙动矫正（最近邻插值和sinc插值）
%%%
%%%Authed  by Piaobo 氵茶花彡
clear;close all;clc;
SNR = -15;                          % 信噪比

c=3e8;
f0 = 9.875e9;                     % 雷达工作频率Hz
lamda = c/f0;                 % 雷达工作波长m
H = 1000;                           % 高度
Yc=2000;                         % 成像区域中线
R0 = sqrt(Yc^2+H^2);       % 中心斜距m

theta = asind(H/R0);          % 下视角
Br=50e6;                           % 带宽
Vr = 200;                           % 雷达有效速度m/s
Tr =5e-6;                          % 脉冲持续时间s
Kr = Br/Tr;                           % 线性调频率
Fr = 1.2*Br;                          % 距离采样频率，1.2为过采样率
Ts = 1/Fr;                             % 距离采样时间间隔s

Nk = ceil((2 * 800/ c + Tr) / Ts);  %距离向前后500m
Nf = 2^nextpow2(Nk);                % 距离向的采样点个数
tf_ori = [-Nf/2:1:Nf/2-1]*Ts;                     % 距离向采样时序
tf = [-Nf/2:1:Nf/2-1]*Ts+2*R0/c;                  % 实际快时间采样值

La = 6;                                                % 等效天线尺寸
Ls = R0*lamda/La;                   % 合成孔径时长度m,Ls=（0.886*R0*lamda）/(La*cos(Theta)）
% Ta = Ls/Vr;                                         % 目标照射时间s
Ta = 0.8;                                         % 目标照射时间s
Ls =Ta*Vr;
Ka = -2 * Vr^2 / (lamda * R0);                          % 方位多普勒调频率Hz
Ba=abs(Ka*Ta);                                             % 多普勒频率调制带宽
PRF = ceil(1.8*Ba);                                       % 方位采样率Hz
% PRF = 1000;                                       % 方位采样率Hz
PRT = 1/PRF;                                      % 方位向采样时间间隔s
Ns = 2^nextpow2((80/Vr+Ta)*PRF);             % 方位向的采样点个数 左右各100m
ts = [-Ns/2 : (Ns/2 - 1)] * PRT;                         % 方位向采样时序
% 理论分辨率
rho_r=c/2/Br;
% rho_a=Vr*PRT;
rho_a=La/2;

% 目标参数
X0 = [-20 20 0 -20 20];                         % 目标1位置坐标
Z0 = [0 0 0 0 0];
Y0 = [Yc+50 Yc+50 Yc Yc-50 Yc-50];
NT=size(X0,2);

%%================================================================
%%生成回波信号
Sb = zeros(Ns,Nf);
sigma = 1; % 回波幅度
for ii=1:NT
    R = sqrt((Vr*ts-X0(ii)).^2+Y0(ii).^2+(Z0(ii)-H).^2);
    tau = 2*R/c;
    Dfast = ones(Ns,1) * tf - tau' * ones(1, Nf);
    phase = pi*Kr*Dfast.^2 - (2 * pi *f0 * tau') * ones(1,Nf);                                           
    Sb = Sb+sigma * exp(1j*phase) .* (abs(Dfast) <= Tr/2) .* ((abs(ts * Vr-X0(ii)) <=Ls/2)' * ones(1,Nf));
end
% Sb = awgn(Sb,SNR,0);                                % 回波加噪

figure
imagesc(real(Sb)),colormap(gray);

%% 距离向压缩
x0 = ones(Ns,1)*(exp(-1j*pi*Kr*(tf_ori).^2).* (abs(tf_ori) <= Tr/2)); % 距离向匹配函数
fftx1 = fftshift(fft(fftshift(x0.'))).'; % 距离向匹配函数FFT
fftSb = fftshift(fft(fftshift(Sb.'))).'; % 原信号FFT
y0 = fftshift(ifft(fftshift((fftSb.*fftx1).'))).';  % 距离向压缩后信号
%显示
ta = ts * Vr;                                     % 方位向的距离序列
tr = tf * c / 2;                                  % 快时间采样对应的距离域(单程距)
% figure;imagesc(tr,ta,abs(y0));colormap(gray);
% axis([tr(Nf/2-Nf/2^8),tr(Nf/2+Nf/2^8),ta(1),ta(end)]);
% xlabel('距离单元(m)');ylabel('方位单元(m)');title('距离向压缩');
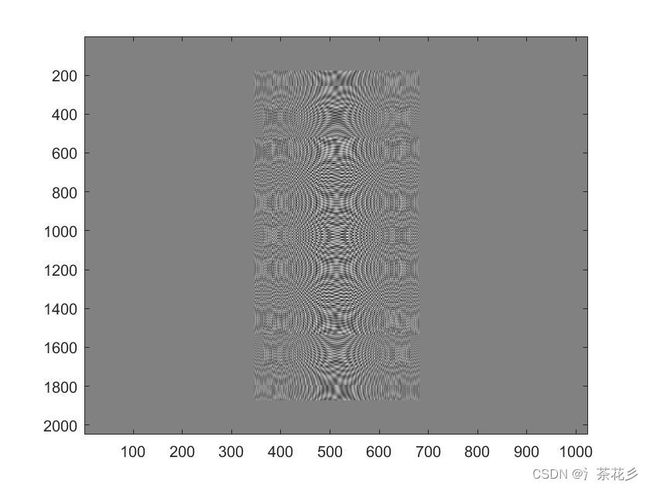
figure;imagesc(abs(y0));colormap(gray);
xlabel('距离向');ylabel('方位向');title('距离向压缩');
 %% 距离徙动矫正1    SINC插值
 

%% 距离徙动矫正2    最近邻插值
 

%% 方位向压缩
ffty0 = fftshift(fft(fftshift(y0))); % 距离向压缩后信号FFT
% x1 = exp(-1j*4*pi/lamda*sqrt((X0-Vr*ts-Bx(1)).^2+(Y0)^2+(Z0-Bz(1)-H)^2))'*ones(1,Nf); % 方位向匹配函数
x1 = exp(1j*pi*(ts.^2)*Ka)'*ones(1,Nf); % 方位向匹配函数
fftx1 = fftshift(fft(fftshift(x1))); % 方位向匹配函数FFT
y1 = fftshift(ifft(fftshift((ffty0.*fftx1)))); % 方位向压缩后信号

figure;imagesc(abs(y1));colormap(gray);
xlabel('距离向');ylabel('方位向');title('方位向压缩');
% xlabel('Range(m)');ylabel('Azimuth(m)');title('Uncompensated');
成像结果如下：

原始信号实部：

 

原始信号虚部：

 

距离压缩结果：

 

方位压缩成像结果(此图未进行距离徙动补偿，非中心目标出现散焦)：

 中心目标的db图（边上有其他目标的扩散能量进来）：