高斯过程回归预测Matlab简单实现
0. 说在前面的话
如果是新手入门高斯过程回归的话建议先读这篇博客才能更好理解下面的程序哟~
快速入门高斯过程回归预测
1. 单点预测例题
- 主程序:
clear
close all
%% 求解程序
x = [-1.5 -1 -0.75 -0.4 -0.25 0];%输入测量完成时间点
y = [-1.6538 -1.0769 -0.2692 -0.2692 0.5923 0.9231];%输入对应时间下实验值
n=length(x);
x_pre=0.2;%输入预测时间点
fangcha_f= 1.27;
fangcha_n=0.3;
l=1;
K=zeros(n,n);
K1=zeros(1,n);
for i=1:n
for j=1:n
K(i,j)=(fangcha_f^2)*exp(-((x(i)-x(j))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x(j));
end
K1(i)=(fangcha_f^2)*exp(-((x(i)-x_pre)^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x_pre);
end
K2=(fangcha_f^2)*exp((-(x_pre-x_pre)^2)/(2*l^2))+(fangcha_n^2)*kronecker(x_pre,x_pre);
y_pre=K1*(K^-1)*y';
fangcha_pre=K2-K1*(K^-1)*K1';
disp(['预测点的均值为',num2str(y_pre)]);
disp(['预测点的方差为',num2str(fangcha_pre)]);
- kronecker函数:两个输入相等输出为1,反之为0
function f=kronecker(i,j)
% Kronecker delta function
if i==j
f=1;
else
f=0;
end
- 似然函数:
function f=fun(x)
m = [-1.5 -1 -0.75 -0.4 -0.25 0];
y = [-1.6538 -1.0769 -0.2692 -0.2692 0.5923 0.9231];
n=length(m);
for i=1:n
for j=1:n
K(i,j)=(x(2)^2)*exp(-((m(i)-m(j))^2)/(2*x(1)^2))+(0.3^2)*kronecker(m(i),m(j));
end
end
f=0.5*y*(K^-1)*y'+0.5*log(det(K));
- 超参数优化函数:使用了matlab中自带的fmincon函数
clc
x0=[1;1];
lb=[0;1];
ub=[1;10];
[x,fval]=fmincon(@fun,x0,[],[],[],[],lb,ub,[])
2. 直接预测法预测5点例题
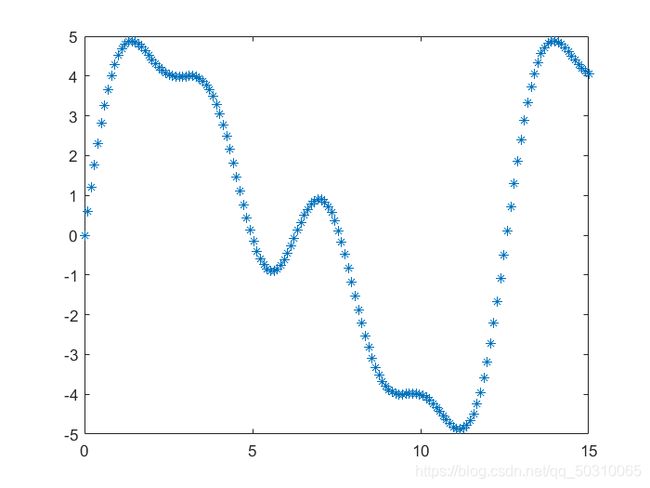
- 构造输入点的函数表达式:
x=linspace(0.1,15,150);
n=length(x);
for i=1:n
y(i)=2*sin(x(i))+sin(2*x(i))+4*sin(x(i)/2);
end
plot(x,y,'*')
- 主程序:
clear
close all
%存放一张你喜欢的颜色方案,与该程序同一文件夹
A=imread('color9.png');
imshow(A)
[yc,xc]=getpts; % 取色,程序一共需要多少种程序就用点选多少个颜色,点一次为一个,需要注意顺序
yc=fix(yc);
xc=fix(xc);
kc=length(xc);
for i=1:1:kc
COLOR(i,:)=A(xc(i),yc(i),:);
end
%% 求解程序
clc
x=linspace(0,15,150);
for i=1:150
y(i)=2*sin(x(i))+sin(2*x(i))+4*sin(x(i)/2);
end
n=length(x);
x_pre=linspace(15.1,15.5,5);%输入预测时间点
m=length(x_pre);
y_pre=zeros(1,m);
fangcha_pre=zeros(1,m);
fangcha_f= 3.9003;
fangcha_n=0.3;
l=1.4289;
%第1个预测点
K1=zeros(n,n);
K1_1=zeros(1,n);
for i=1:n
for j=1:n
K1(i,j)=(fangcha_f^2)*exp(-((x(i)-x(j))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x(j));
end
K1_1(i)=(fangcha_f^2)*exp(-((x(i)-x_pre(1))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x_pre(1));
end
K1_2=(fangcha_f^2)*exp((-(x_pre(1)-x_pre(1))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x_pre(1),x_pre(1));
y_pre(1)=K1_1*(K1^-1)*y';
fangcha_pre(1)=K1_2-K1_1*(K1^-1)*K1_1';
%第2个预测点
K2=zeros(n,n);
K2_1=zeros(1,n);
for i=1:n
for j=1:n
K2(i,j)=(fangcha_f^2)*exp(-((x(i)-x(j))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x(j));
end
K2_1(i)=(fangcha_f^2)*exp(-((x(i)-x_pre(2))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x_pre(2));
end
K2_2=(fangcha_f^2)*exp((-(x_pre(2)-x_pre(2))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x_pre(2),x_pre(2));
y_pre(2)=K2_1*(K2^-1)*y';
fangcha_pre(2)=K2_2-K2_1*(K2^-1)*K2_1';
%第3个预测点
K3=zeros(n,n);
K3_1=zeros(1,n);
for i=1:n
for j=1:n
K3(i,j)=(fangcha_f^2)*exp(-((x(i)-x(j))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x(j));
end
K3_1(i)=(fangcha_f^2)*exp(-((x(i)-x_pre(3))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x_pre(3));
end
K3_2=(fangcha_f^2)*exp((-(x_pre(3)-x_pre(3))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x_pre(3),x_pre(3));
y_pre(3)=K3_1*(K3^-1)*y';
fangcha_pre(3)=K3_2-K3_1*(K3^-1)*K3_1';
%第4个预测点
K4=zeros(n,n);
K4_1=zeros(1,n);
for i=1:n
for j=1:n
K4(i,j)=(fangcha_f^2)*exp(-((x(i)-x(j))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x(j));
end
K4_1(i)=(fangcha_f^2)*exp(-((x(i)-x_pre(4))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x_pre(4));
end
K4_2=(fangcha_f^2)*exp((-(x_pre(4)-x_pre(4))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x_pre(4),x_pre(4));
y_pre(4)=K4_1*(K4^-1)*y';
fangcha_pre(4)=K4_2-K4_1*(K4^-1)*K4_1';
%第5个预测点
K5=zeros(n,n);
K5_1=zeros(1,n);
for i=1:n
for j=1:n
K5(i,j)=(fangcha_f^2)*exp(-((x(i)-x(j))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x(j));
end
K5_1(i)=(fangcha_f^2)*exp(-((x(i)-x_pre(5))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x(i),x_pre(5));
end
K5_2=(fangcha_f^2)*exp((-(x_pre(5)-x_pre(5))^2)/(2*l^2))+(fangcha_n^2)*kronecker(x_pre(5),x_pre(5));
y_pre(5)=K5_1*(K5^-1)*y';
fangcha_pre(5)=K5_2-K5_1*(K5^-1)*K5_1';
disp(['预测点的均值为',num2str(y_pre)]);
disp(['预测点的方差为',num2str(fangcha_pre)]);
%% 画图程序
COLOR1=COLOR(1,:);
COLOR2=COLOR(2,:);
COLOR3=COLOR(3,:);
x_after=zeros(1,n+m);
y_after=zeros(1,n+m);
fangcha_after=zeros(1,n+m);
x_after=[x,x_pre];
y_after=[y,y_pre];
for i=1:n
fangcha(i)=0.09;
end
fangcha_after=[fangcha,fangcha_pre];
for i=1:n+m
zhixindu_shang(i)=y_after(i)+1.96*(fangcha_after(i)^0.5);%置信度上限
zhixindu_xia(i)=y_after(i)-1.96*(fangcha_after(i)^0.5);%置信度下限
end
p1=fill([x_after,fliplr(x_after)],[zhixindu_xia,fliplr(zhixindu_shang)],'r');%FaceColor为填充颜色,EdgeColor为边框颜色
p1.FaceColor = COLOR1;%定义区间的填充颜色
p1.EdgeColor = COLOR3;%定义区间边界的填充颜色,此处不设置
hold on
plot(x_after,y_after,'r-','MarkerSize',6,'linewidth',1.2,'color',COLOR2)
hold on
plot(x_pre,y_pre,'b-','MarkerSize',6,'linewidth',2)
hold on
xlabel('x','FontSize',8,'FontWeight','bold');
ylabel('y','FontSize',8,'FontWeight','bold');
- kronecker函数:两个输入相等输出为1,反之为0
function f=kronecker(i,j)
% Kronecker delta function
if i==j
f=1;
else
f=0;
end
- 似然函数:
function f=fun(t)
x=linspace(0,15,150);
n=length(x);
for i=1:n
y(i)=2*sin(x(i))+sin(2*x(i))+4*sin(x(i)/2);
end
for i=1:n
for j=1:n
K(i,j)=(t(2)^2)*exp(-((x(i)-x(j))^2)/(2*t(1)^2))+(0.3^2)*kronecker(x(i),x(j));
end
end
f=0.5*y*(K^-1)*y'+0.5*log(det(K));
- 超参数优化函数:使用了matlab中自带的fmincon函数
clc
lb=[0;0];
ub=[200;10];
t_0=[1;1];
[t,fval]=fmincon(@fun,t_0,[],[],[],[],lb,ub,[])
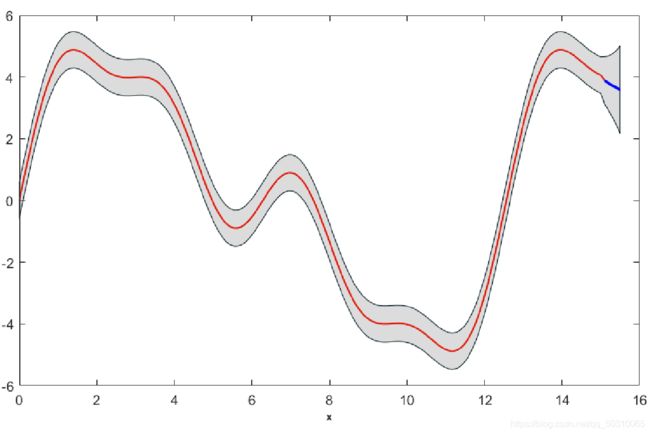
- 预测结果图:
3. 结尾
这两个程序只是自己通过高斯过程的理解进行简单编程实现的,不足以解决复杂的预测问题:如输入二维输出一维等;建议复杂的预测可使用相关的工具包进行学习~