文本识别论文CRNN
目录
- 1. 解读文本识别论文CRNN
-
- 1.1 CRNN文字识别整体流程
- 1.2 理解CTC Loss
-
- 1.2.1 CTC loss是如何做的
- 1.2.2 以一个具体的例子来展现CTC loss的过程
- 2. 总结
- 3. 参考资料
1. 解读文本识别论文CRNN
本文解读的是一篇来自2015年的一篇文字识别论文 [ 1 ] ^{[1]} [1]。里面的CTC Loss相关内容的理解有一定的挑战性,本文是对自己当前理解的一份记录。
1.1 CRNN文字识别整体流程
首先,先看一下CRNN的前向推理过程,来了解其文字识别的整体流程,如下图所示。

action1 : 一张 10 ∗ 40 ∗ 3 10*40*3 10∗40∗3的文字图片块,经过CNN层特征提取,下采样为 1 ∗ 10 ∗ 512 1*10*512 1∗10∗512的特征图。高度压缩为1,宽度下采样4倍,每一个特征是维度为512。
action2 : 通过深度双向LSTM网络将 10 ∗ 512 10*512 10∗512的Feature sequence做了一个特征的进一步转换和提取变为一个 10 ∗ ( 26 + 1 ) 10*(26+1) 10∗(26+1)的预测分布概率矩阵。这里使用双向LSTM是期待特征序列做更加充分的贯通,例如在预测“state”
中“a”的时候既采纳了“st”的信息又采纳了"te"的信息。
action3 : 通过转录层操作,根据分布概率矩阵可以获得最终的预测结果。例如 a r g m a x ( y , d i m = 1 ) argmax(y, dim=1) argmax(y,dim=1),可以得到预测值的初始形态:
| - | s | - | t | - | a | a | t | t | e |
|---|
然后合并成为最终的预测结果: state。合并的基本规则是:
- 属于占位符所割出来的同一个block中,如果有紧邻的相同元素进行合并。
- 消除占位符。
前向推理过程比较明晰,然而,训练过程会遇到如下疑惑,如果按照上述例子,我们会把这一个序列作为预测概率矩阵 y y y的GT。然后就相当于并行做10个(26+1)类的分类任务学习。
| - | s | - | t | - | a | a | t | t | e |
|---|
这样的问题在于:
抛出问题1 : 对于同一张图片可以有不同的GT方案。
例如,下列序列作为“state”对应的的分布概率矩阵GT,也是不违背任何逻辑的。事实上,这种不违背逻辑的方案还有很多。
| - | - | s | t | - | a | a | t | t | e |
|---|
尝试解决问题1 :尝试列举出所有可能的方案, 在训练的过程中随机给出一个gt。
这样做理论上是可行的。但是会有一个时间复杂度问题。采用暴力求解的方法罗列出所有可能是 ( 26 + 1 ) 10 (26+1)^{10} (26+1)10。即使模型的最大预测字符串长度为10,仅为26个字母这种简易场景,这种级别的时间复杂度是不可以接受的。
但不管怎样,至此,上述整个过程是一种理论上完备的训练、推理流程,只不过训练速度会很慢(或者说慢到不可接受)。
1.2 理解CTC Loss
1.2.1 CTC loss是如何做的
CTC Loss 或者说CTC 算法是来源于HMM(隐马尔可夫),用一句话总结:就是通过“动态规划”算法来替代“暴力求解”来解决所有方案的概率和。并将问题的loss定义为一个最大似然问题:使得学到尽可能的网络参数使得 p ( l x ) p(\frac{l}{x}) p(xl)最大,论文中将loss定义为 − l o g ( p ( l x ) ) -log(p(\frac{l}{x})) −log(p(xl))。CTC的过程可以总结为以下四步骤:
- p ( l x ) = ∑ s = 1 s = 2 ∣ l ∣ + 1 α t ( s ) ∗ β t ( s ) y t ( s ) p(\frac{l}{x}) = \sum_{s=1}^{s=2|l|+1} \frac{\alpha_t(s)*\beta_t(s)}{y_{t}(s)} p(xl)=∑s=1s=2∣l∣+1yt(s)αt(s)∗βt(s)
- y y y概率矩阵—>计算 α 矩阵 \alpha矩阵 α矩阵, β \beta β矩阵—> 计算 p ( l x ) 计算p(\frac{l}{x}) 计算p(xl)
- α \alpha α矩阵的计算是通过动态规划算法由 y y y来计算的。

- β \beta β矩阵的计算是通过动态规划由 y y y来计算的。
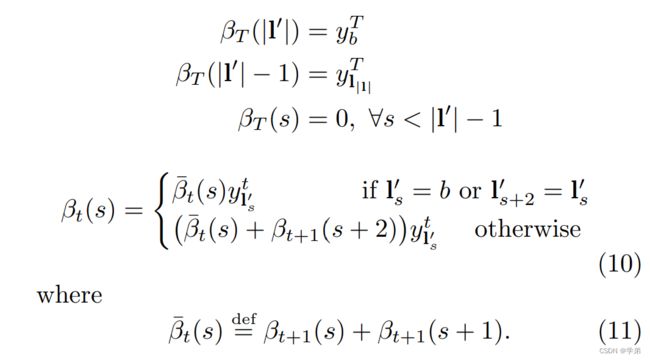
1.2.2 以一个具体的例子来展现CTC loss的过程
以下例子来自于torch官网。为了便于描述,将参数的规模进行了缩小。
>>> import torch
>>> import torch.nn as nn
>>> # Target are to be padded
>>> T = 5 # torch 官网为50 # Input sequence length
>>> C = 7 # torch 官网为20 # Number of classes (including blank, 0 class)
>>> N = 1 # torch 官网为16 # Batch size
>>> S = 3 # 30 # Target sequence length of longest target in batch (padding length)
>>> S_min = 2 # 10 # Minimum target length, for demonstration purposes
>>>
>>> # Initialize random batch of input vectors, for *size = (T,N,C)
>>> input = torch.randn(T, N, C).log_softmax(2).detach().requires_grad_()
>>>
>>> # Initialize random batch of targets (0 = blank, 1:C = classes)
>>> target = torch.randint(low=1, high=C, size=(N, S), dtype=torch.long)
>>>
>>> input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
>>> target_lengths = torch.randint(low=S_min, high=S, size=(N,), dtype=torch.long)
>>> ctc_loss = nn.CTCLoss()
>>> loss = ctc_loss(input, target, input_lengths, target_lengths)
>>> loss.backward()
其中,input表示的是预测概率的 l o g log log矩阵:
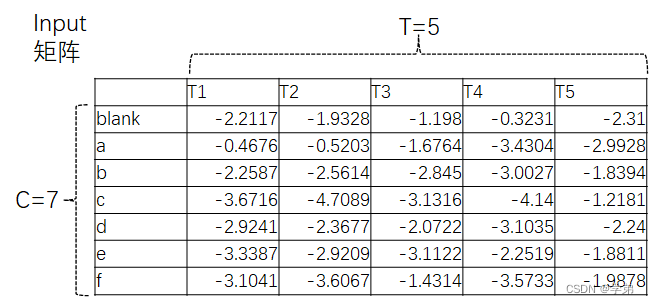
预测概率矩阵 y = e i n p u t y=e^{input} y=einput,如下所示:
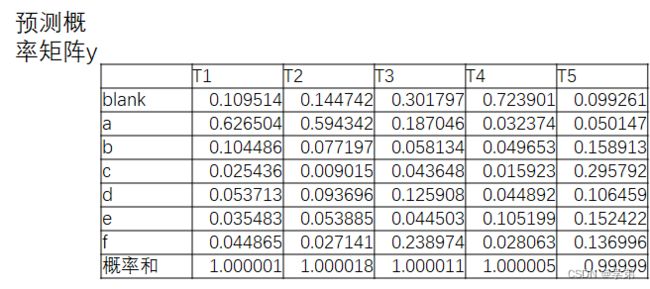
举一个简单的例子target为 f e fe fe: 根据1.2.1节中步骤3可以根据 y y y矩阵动态递归算得 α s ( t ) α_s(t) αs(t)矩阵:
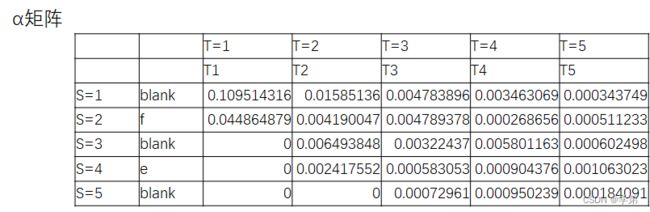
根据1.2.2节,步骤4可以根据 y y y矩阵动态递归算得 β s ( t ) β_s(t) βs(t)矩阵:
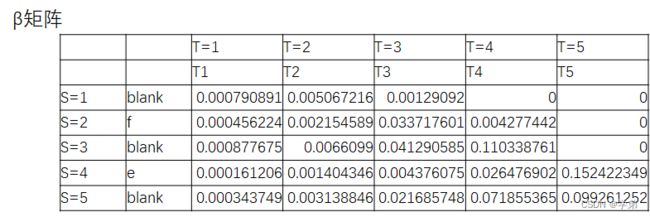
根据1.2.1节中步骤1可以根据α矩阵和β矩阵计算得到两者的联合概率:
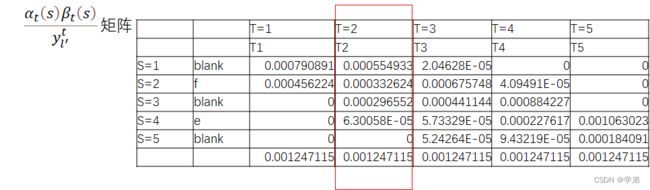
l o s s = − l o g ( 0.001247115 / 3 ) = 3.38 loss = -log(0.001247115/3)=3.38 loss=−log(0.001247115/3)=3.38, 与pytorch的输出一致。
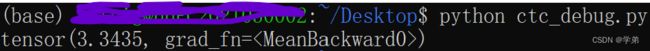
2. 总结
本文主要以CTC是如何做的角度来写,并通过pytorch和自己手算结果的对比来验证自己理解的正确性。后续如果有新的理解,应该会补充上一些更多的细节。
3. 参考资料
[1] 原始论文:An End-to-End Trainable Neural Network for Image-based Sequence Recognition and Its Application to Scene Text Recognition
[2]Pytorch ctc demo example
[3]公式