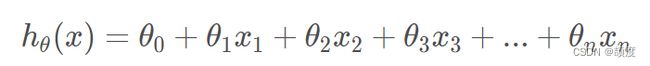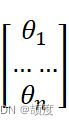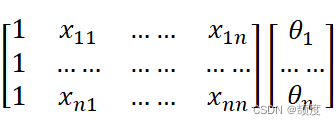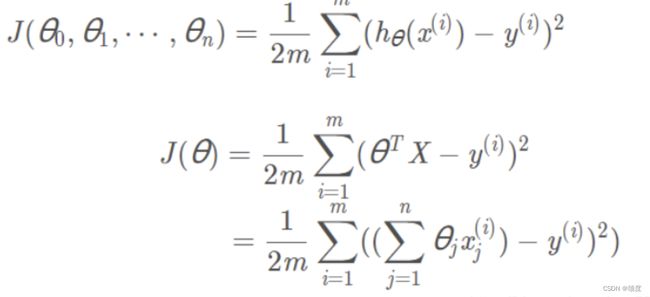多元线性回归模型
目录:
一、引言
二、理想场景的预设
三、多元线性回归模型
四、鸢尾花数据集
一、引言:
多元线性回归是一元线性回归的多维运用。在一元线性回归中,我们用自变量系数表示对自变量与因变量之间的解释因素。那么,在多元线性回归中,我们引入多个解释变量,对同一个个体在不同方面的解释进行多维度的衡量。
二、理想场景的预设:
为了便于理解,我们可以假设有一幢楼进行售卖,用y表示房子的房价,x表示这间房子的不同解释因素,如:面积、位置、采光度、装修等等(影响一间房子的价格绝不仅仅是面积的大小,因此这样的解释是合理的)。
那么,我们就要列举出一个能够综合评判房屋价格的一个数学模型,通过不同维度的计量,从而得到一个能够较全面衡量一间房屋综合价值的数值(类似于国民GDP)。
由此,我们便引入了多元线性回归模型,为了便于观察,我们还引入了基于矩阵运算的模型分析。
三、多元线性回归模型
模型引入:
通常情况下,一般的多元回归模型写法很多,例如:
这样写太过于繁杂,并且在实际求解的过程中并不能简化我们的运算。为此,引入矩阵运算。
推导损失函数:
运用梯度下降:
四、鸢尾花数据集
Iris 鸢尾花数据集内包含 3 类,分别为山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica),共 150 条记录,每类各 50 个数据,每条记录都有 4 项特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度,可以通过这 4 个特征预测鸢尾花卉属于哪一品种。 这是本文章所使用的鸢尾花数据集: sl:花萼长度 ;sw:花萼宽度 ;pl:花瓣长度 ;pw:花瓣宽度; type:类别:(Iris-setosa、Iris-versicolor、Iris-virginica 三类)
部分展示:
代码:
import pandas as pd
import numpy as np
import time
import random
def MGD_train(X, y, alpha=0.0001, maxIter=1000, theta_old=None):
'''
MGD训练线性回归
传入:
X : 已知数据
y : 标签
alpha : 学习率
maxIter : 总迭代次数
返回:
theta : 权重参数
'''
# 初始化权重参数
theta = np.ones(shape=(X.shape[1],))
if not theta_old is None:
# 假装是断点续训练
theta = theta_old.copy()
# axis=1 表示横轴,方向从左到右;axis=0 表示纵轴,方向从上到下
for i in range(maxIter):
# 预测
y_pred = np.sum(X * theta, axis=1)
# 全部数据得到的梯度
gradient = np.average((y - y_pred).reshape(-1, 1) * X, axis=0)
# 更新学习率
theta += alpha * gradient
return theta
def SGD_train(X, y, alpha=0.0001, maxIter=1000, theta_old=None):
'''
SGD训练线性回归
传入:
X : 已知数据
y : 标签
alpha : 学习率
maxIter : 总迭代次数
返回:
theta : 权重参数
'''
# 初始化权重参数
theta = np.ones(shape=(X.shape[1],))
if not theta_old is None:
# 假装是断点续训练
theta = theta_old.copy()
# 数据数量
data_length = X.shape[0]
for i in range(maxIter):
# 随机选择一个数据
index = np.random.randint(0, data_length)
# 预测
y_pred = np.sum(X[index, :] * theta)
# 一条数据得到的梯度
gradient = (y[index] - y_pred) * X[index, :]
# 更新学习率
theta += alpha * gradient
return theta
def MBGD_train(X, y, alpha=0.0001, maxIter=1000, batch_size=10, theta_old=None):
'''
MBGD训练线性回归
传入:
X : 已知数据
y : 标签
alpha : 学习率
maxIter : 总迭代次数
batch_size : 没一轮喂入的数据数
返回:
theta : 权重参数
'''
# 初始化权重参数
theta = np.ones(shape=(X.shape[1],))
if not theta_old is None:
# 假装是断点续训练
theta = theta_old.copy()
# 所有数据的集合
all_data = np.concatenate([X, y.reshape(-1, 1)], axis=1)
for i in range(maxIter):
# 从全部数据里选 batch_size 个 item
X_batch_size = np.array(random.choices(all_data, k=batch_size))
# 重新给 X, y 赋值
X_new = X_batch_size[:, :-1]
y_new = X_batch_size[:, -1]
# 将数据喂入,更新 theta
theta = MGD_train(X_new, y_new, alpha=0.0001, maxIter=1, theta_old=theta)
return theta
def GD_predict(X, theta):
'''
用于预测的函数
传入:
X : 数据
theta : 权重
返回:
y_pred: 预测向量
'''
y_pred = np.sum(theta * X, axis=1)
# 实数域空间 -> 离散三值空间,则需要四舍五入
y_pred = (y_pred + 0.5).astype(int)
return y_pred
def calc_accuracy(y, y_pred):
'''
计算准确率
传入:
y : 标签
y_pred : 预测值
返回:
accuracy : 准确率
'''
return np.average(y == y_pred) * 100
# 读取数据
iris_raw_data = pd.read_csv('iris.data', names =['sepal length', 'sepal width', 'petal length', 'petal width', 'class'])
# 将三种类型映射成整数
Iris_dir = {'Iris-setosa': 1, 'Iris-versicolor': 2, 'Iris-virginica': 3}
iris_raw_data['class'] = iris_raw_data['class'].apply(lambda x:Iris_dir[x])
# 训练数据 X
iris_data = iris_raw_data.values[:, :-1]
# 标签 y
y = iris_raw_data.values[:, -1]
# 用 MGD 训练的参数
start = time.time()
theta_MGD = MGD_train(iris_data, y)
run_time = time.time() - start
y_pred_MGD = GD_predict(iris_data, theta_MGD)
print("MGD训练1000轮得到的准确率{:.2f}% 运行时间是{:.2f}s".format(calc_accuracy(y, y_pred_MGD), run_time))
# 用 SGD 训练的参数
start = time.time()
theta_SGD = SGD_train(iris_data, y)
run_time = time.time() - start
y_pred_SGD = GD_predict(iris_data, theta_SGD)
print("SGD训练1000轮得到的准确率{:.2f}% 运行时间是{:.2f}s".format(calc_accuracy(y, y_pred_SGD), run_time))
# 用 MBGD 训练的参数
start = time.time()
theta_MBGD = MBGD_train(iris_data, y)
run_time = time.time() - start
y_pred_MBGD = GD_predict(iris_data, theta_MBGD)
print("MBGD训练1000轮得到的准确率{:.2f}% 运行时间是{:.2f}s".format(calc_accuracy(y, y_pred_MBGD), run_time))结果: