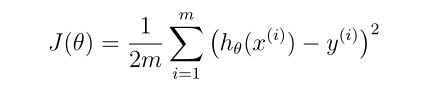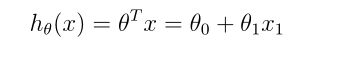吴恩达机器学习作业一：利用多元线性回归模型实现房价预测（python实现）

吴恩达机器学习作业一：利用多元线性回归模型实现房价预测（python实现）

该文是针对吴恩达机器学习作业任务二和任务三中，利用多元线性回归模型实现房价预测以及使用正规方程求得最佳theta的取值，使代价值最小，对于任务一利用单变量线线性回归模型实现餐车利润预测见博客：传送门

任务

In this part, you will implement linear regression with multiple variables to
predict the prices of houses. Suppose you are selling your house and you
want to know what a good market price would be. One way to do this is to
first collect information on recent houses sold and make a model of housing
prices.
The file ex1data2.txt contains a training set of housing prices in Port-
land, Oregon. The first column is the size of the house (in square feet), the
second column is the number of bedrooms, and the third column is the price
of the house.
利用多元线性回归模型预测房价，给出的训练数据集中包括房子面积，卧室数量，房价。
由于房子的大小是卧室数量的1000倍，因此需要将所有的训练数据进行归一化处理。
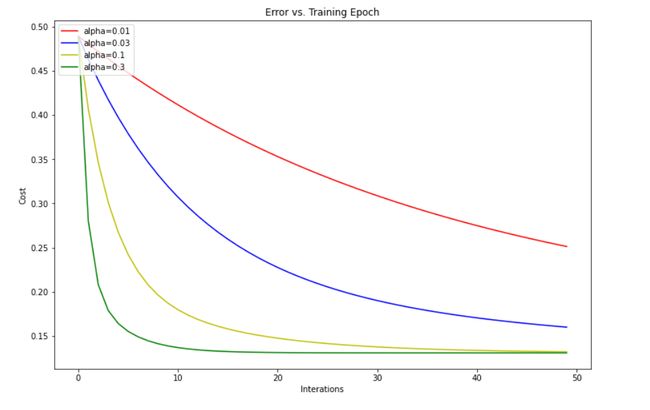
学习率alpha的取值不同，在运行梯度下降算法时，效果不同，在该任务重分别设置alpha[0.01,0.03,0.1,0.3],计算在迭代50次下，代价值的变换情况，并绘制图片进行展示。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#读取数据
path_file="../code/ex1-linear regression/ex1data2.txt"
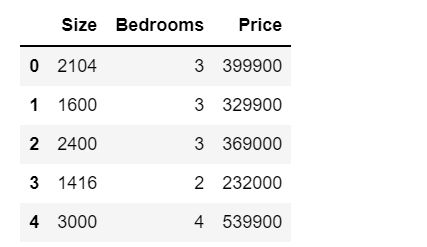
data=pd.read_csv(path_file,names=['Size', 'Bedrooms', 'Price'])
data.head()

归一化处理

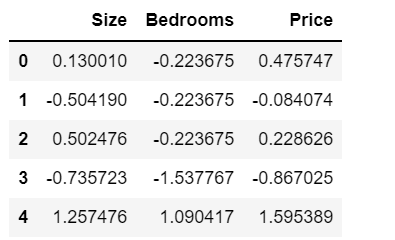
这里采用的是Z-score标准化方法，即给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1。

#归一化处理
data=(data-data.mean())/data.std()
data.head()

初始化值的设置

对于x0的值都为1，因此需要在训练数据的第一列添加一列，值为1
学习率设定为[0.01,0.03,0.1,0.3],theta初始化值设为0，迭代次数设为50次，m表示总共有多少个输入行

data.insert(0,"ones",1)
#data.head()
theta=np.zeros((1,X.shape[1]))
print(theta)
alpha=np.array([0.01,0.03,0.1,0.3])
print(alapha)
iters=50
m=X.shape[0]
col=data.shape[1]
X=np.array(data.iloc[:,0:col-1])
Y=np.array(data.iloc[:,col-1:col])

代价函数的计算

def computeCost(X,Y,theta):
    erros=np.power(np.dot(X,(theta.T))-Y,2)
    return np.sum(erros)/(2*len(erros))
computeCost(X,Y,theta)

0.48936170212765967

梯度下降算法

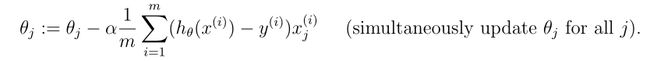
因为最后需要绘制学习率在取不同值的情况下，代价值随迭代次数的变化，因此需要利用cost_list将不同学习率下每次迭代后的代价值存储起来,cur_cost表示当前alpha取值下，每次迭代下代价的取值。

def gradientDescent(X,Y,theta,iters,alpha):
    cur_cost=np.zeros((1,iters))
    for i in range(iters):
        cur_cost[0,i]=computeCost(X,Y,theta)
        error=np.dot(X,(theta.T))-Y
        temp=np.dot(error.T,X)
        #print(temp)
        theta=theta-alpha*temp/m
        #print(theta)
    return theta,cur_cost


costs_list=np.zeros((4,iters)) 
#学习率alpha不同的取值
for i in range(len(alpha)):
    cur_theta,cur_cost=gradientDescent(X,Y,theta,iters,alpha[i])
    costs_list[i]=cur_cost

绘制图谱，观察学习取不同值时，随着迭代次数的增加，代价值的变化速度

def drawFigure(inters,costs_list):
    fig,ax=plt.subplots(figsize=(12,8))
    ax.plot(inters,costs_list[0],'r',label='alpha=0.01')
    ax.plot(inters,costs_list[1],'b',label='alpha=0.03')
    ax.plot(inters,costs_list[2],'y',label='alpha=0.1')
    ax.plot(inters,costs_list[3],'g',label='alpha=0.3')
    ax.legend(loc=2)
    ax.set_xlabel('Interations')
    ax.set_ylabel('Cost')
    ax.set_title('Error vs. Training Epoch')
    plt.show()
drawFigure(np.arange(iters),costs_list)

正规方程求解

利用正规方程求解最佳theta

def compute_theta(X,Y):
    theta=np.linalg.inv(np.dot(X.T,X)).dot(X.T).dot(Y)
    return theta
theta=compute_theta(X,Y)
cost=computeCost(X,Y,theta.T)
print(cost)

0.13068648053904197

全部代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#代价函数
def computeCost(X,Y,theta):
    erros=np.power(np.dot(X,(theta.T))-Y,2)
    return np.sum(erros)/(2*len(erros))
    
#梯度下降算法
def gradientDescent(X,Y,theta,iters,alpha):
    cur_cost=np.zeros((1,iters))
    for i in range(iters):
        cur_cost[0,i]=computeCost(X,Y,theta)
        error=np.dot(X,(theta.T))-Y
        temp=np.dot(error.T,X)
        #print(temp)
        theta=theta-alpha*temp/m
        #print(theta)
    return theta,cur_cost

#绘制图谱，观察学习取不同值时，随着迭代次数的增加，代价值的变化速度
def drawFigure(inters,costs_list):
    fig,ax=plt.subplots(figsize=(12,8))
    ax.plot(inters,costs_list[0],'r',label='alpha=0.01')
    ax.plot(inters,costs_list[1],'b',label='alpha=0.03')
    ax.plot(inters,costs_list[2],'y',label='alpha=0.1')
    ax.plot(inters,costs_list[3],'g',label='alpha=0.3')
    ax.legend(loc=2)
    ax.set_xlabel('Interations')
    ax.set_ylabel('Cost')
    ax.set_title('Error vs. Training Epoch')
    plt.show()
    
#正规方程计算
def normalEqn(X,Y):
    theta=np.linalg.inv(np.dot(X.T,X)).dot(X.T).dot(Y)
    cost=computeCost(X,Y,theta.T)
    return theta,cost
#读取数据
path_file="../code/ex1-linear regression/ex1data2.txt"
data=pd.read_csv(path_file,names=['Size', 'Bedrooms', 'Price'])

#归一化处理
data=(data-data.mean())/data.std()

#数据预处理
data.insert(0,"ones",1)
#data.head()
theta=np.zeros((1,X.shape[1]))
#print(theta)
alpha=np.array([0.01,0.03,0.1,0.3])
#print(alapha)
iters=50
m=X.shape[0]
col=data.shape[1]
X=np.array(data.iloc[:,0:col-1])
Y=np.array(data.iloc[:,col-1:col])
#利用cost_list将不同学习率下每次迭代后的代价值存储起来,cur_cost表示当前alpha取值下，每次迭代下代价的取值。
costs_list=np.zeros((4,iters)) 
#学习率alpha不同的取值
for i in range(len(alpha)):
    cur_theta,cur_cost=gradientDescent(X,Y,theta,iters,alpha[i])
    costs_list[i]=cur_cost
#绘制图片
drawFigure(np.arange(iters),costs_list)

#正规方程求最佳theta值
theta,cost=normalEqn(X,Y)
print(theta)
print(cost)