数学建模学习：蒙特卡洛模拟

本文作者：小季不是咸鱼(知乎ID)，答学百科(公众号)

引言

为什么我要先讲蒙特卡洛模拟？

  我认为蒙特卡洛模拟是一种数学思想，类似于数形结合、方程思想？

  为什么这么说？

  当一道数学问题从理论上很难阐明的时候，我们可以画个图，很容易解释清楚，这叫数形结合；从理论上很难理解的题目，我们通过列方程，很容易解决问题，这叫方程思想。

  因此，当我们从理论上很难解释很难解决一个问题时，我们可以利用计算机进行大量模拟来解决，这就叫蒙特卡洛模拟。

  再次强调：蒙特卡洛模拟只是教会你一种数学思维，而不是一种固定的套路！！！

  历年国赛有五个优秀论文都用到了蒙特卡洛模拟！

一、 蒙特卡罗模拟概述

  蒙特卡罗方法又称随机抽样技巧或统计试验方法。 (英文名Monte Carlo)

  它是用来解决数学和物理问题的非确定性的（概率统计的或随机的）数值方法。 因此Monte Carlo 方法（MCM），也称为统计试验方法。

  它是用一系列随机数来近似解决问题的一种方法，是通过寻找一个概率统计的相似体并用实验取样过程来获得该相似体的近似解的处理数学问题的一种手段。运用该近似方法所获得的问题的解更接近于物理实验结果，而不是经典数值计算结果。

  用通俗易懂的话来说，蒙特卡洛模拟就是通过计算机产生大量的样本来进行模拟，用离散的代替连续的，用频率代替概率。

  原理：由大数定理可知，当样本容量足够大时，事件发生的频率即为概率。

二、 简单的例子：蒲丰投针问题

2.1 蒲丰投针问题的提出

  为了求得圆周率 $\pi$ 值，在十九世纪后期，有很多人作了这样的试验：将长为 $l$ 的一根针任意投到地面上，用针与一组相间距离为 $a$$(l<a)$ 的平行线相交的频率代替概率 $P$ ，如图1所示

  再利用准确的关系式：
$$P=\frac{2l}{\pi a}$$
  求出 $\pi$ 值
$$\pi =\frac{2l}{aP}\approx \frac{2l}{a}\left(\frac{N}{n}\right)$$

  其中 $N$ 为投计次数，$n$ 为针与平行线相交次数。这就是古典概率论中著名的蒲丰投针问题。但当时没有计算机，因此只能通过人为的投掷实验，来求出 $\pi $ 值

2.2 蒲丰投针问题的详细分析

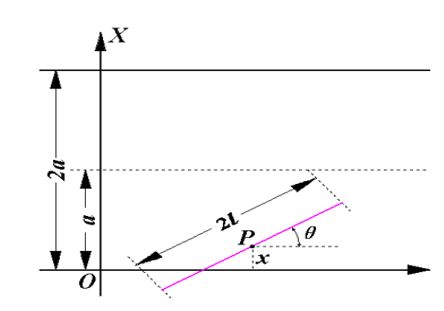
  设针投到地面上的位置可以用一组参数$\left( x,\theta \right)
$来描述， $x$ 为针中心的坐标， $\theta $ 为针与平行线的夹角，如下图所示(注意，下图所示的 $2a$ 应为 $a$ , $2l$ 应为 $l$)。

  任意投针，就是意味着 $x$与$\theta $都是任意取的，但$x $的范围限于$\left[ 0,a \right] $，夹角$\theta $的范围限于$\left[ 0,\pi \right] $。在此情况下，针与平行线相交的数学条件是
$$x\le l\cdot \sin \theta$$

  满足这一关系式的区域记为$g$,如图3所示，于是我们的问题等价于在区域$G$中任意投掷一点，而该点落入区域$g$的概率，由几何概率的定义，所求概率为
$$P=\frac{\text{区域}g\text{的面积}}{\text{区域}G\text{的面积}}=\frac{{\int }_0^{\pi }\frac{l}{2}\sin \theta \mathrm{d}\theta }{\frac{l}{2}a\pi }=\frac{2l}{\pi a}$$

2.3 蒲丰投针模拟的MATLAB代码

  下面让我们用MATLAB来模拟一下投针实验

clear;clc
l =  0.520;     % 针的长度（任意给的）
a = 1.314;    % 平行线的宽度(大于针的长度l即可)
n = 1000;    % 做n次投针试验，n越大求出来的pi越准确，当然由于计算机运行时间不能太长，因此不能过于大
m = 0;    % 记录针与平行线相交的次数
x = rand(1, n) * a / 2 ;   % 在[0, a/2]内服从均匀分布随机产生n个数， x中每一个元素表示针的中点和最近的一条平行线的距离
phi = rand(1, n) * pi;    % 在[0, pi]内服从均匀分布随机产生n个数，phi中的每一个元素表示针和最近的一条平行线的夹角
axis([0,pi, 0,a/2]);   box on;  % 画一个坐标轴的框架，x轴位于0-pi，y轴位于0-a/2， 并打开图形的边框
for i=1:n  % 开始循环，依次看每根针是否和直线相交
    if x(i) <= l / 2 * sin(phi (i))     % 如果针和平行线相交
        m = m + 1;    % 那么m就要加1
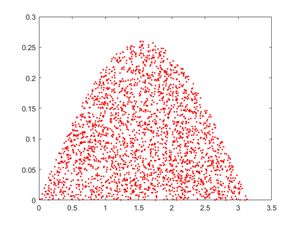
        plot(phi(i), x(i), 'r.')   % 模仿书上的那个图，横坐标为phi，纵坐标为x , 用红色的小点进行标记
        hold on  % 在原来的图形上继续绘制
    end
end

  得到的结果如下：

蒙特卡罗方法得到pi为：3.1812

  因为随机数是由计算机产生的，因此每一次输出的结果都可能相同，并且n的值越大，结果越接近真实值，为了提高准确性，我们可以利用MATLAB的for循环模拟100次（或者更多次），最后求平均值得到结果

% 由于一次模拟的结果具有偶然性，因此我们可以重复100次后再来求一个平均的pi
result = zeros(100,1);  % 初始化保存100次结果的矩阵
l =  0.520;     a = 1.314;
n = 1000000;    
for num = 1:100
    m = 0;  
    x = rand(1, n) * a / 2 ;
    phi = rand(1, n) * pi;
    for i=1:n
        if x(i) <= l / 2 * sin(phi (i))
            m = m + 1;
        end
    end
    p = m / n;
    mypi = (2 * l) / (a * p);
    result(num) = mypi;  % 把求出来的myphi保存到结果矩阵中
end
mymeanpi = mean(result);  % 计算result矩阵中保存的100次结果的均值
disp(['蒙特卡罗方法得到pi为：', num2str(mymeanpi)])

  此时输出的结果会更加接近pi值

2.4 蒲丰投针实验结论

  由蒲丰试验可以看出，当所求问题的解是某个事件的概率，或者是某个随机变量的数学期望，或者是与概率、数学期望有关的量时，通过某种试验的方法，得出该事件发生的频率，或者该随机变量若干个具体观察值的算术平均值，通过它得到问题的解。这就是蒙特卡罗方法的基本思想。

三、 蒙特卡洛模拟的一般步骤

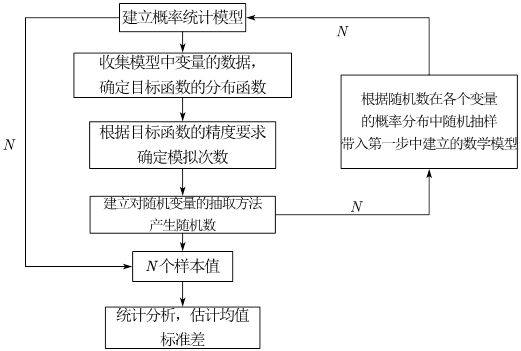
3.1 蒙特卡洛模拟的流程图

  下面流程图可以根据题意写在论文中，但是一定要结合实际题目

3.2 一个简单的例子

3.2.1 问题提出

  某投资项目每年所得盈利额A由投资额P、劳动生产率L、和原料及能源价格Q三个因素决定。
$$A=aP+b{L}^2+c{Q}^{\frac{1}{2}}+d$$

  现在想根据历史数据，预测未来。

3.2.2 问题分析

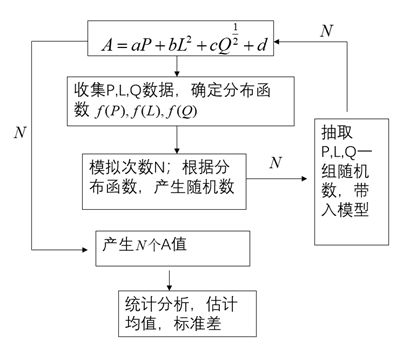
  问题解决的流程图

  其实这里面说的对未来进行预测可能不是我们想象中的对变量和目标随时间的变化做出预测，说实话这个题出的并不好，我只是想在此举一个例子罢了。

  这个流程图是什么意思呢？

  我们得到了P,L,Q的大量历史数据，可以从历史的数据中得到均值、标准差、方差、最大最小值等等一系列的统计变量，然后我们通过计算机，按照历史的这些均值、标准差等统计变量再重新模拟出未来的大量样本，通过未来的大量样本，再次利用$A=aP+b{L}^2+c{Q}^{\frac{1}{2}}+d$，得到未来的A的一系列均值、标准差、方差等统计因素，达到我们的目的

四、 蒙特卡洛模拟的优缺点

4.1 优点

• 能够比较逼真地描述具有随机性质的事物的特点及物理实验过程。
• 受几何条件限制小。
• 收敛速度与问题的维数无关。
• 具有同时计算多个方案与多个未知量的能力。
• 误差容易确定。
• 程序结构简单，易于实现。

4.2 缺点

• 收敛速度慢。
• 误差具有概率性。
• 在粒子输运问题中，计算结果与系统大小有关。

4.3 解释说明

  一般来说，在下列情况是计算机模拟更能有效的解决问题：

• 数学公式难以表示的系统，或者没有有效的方法解决数学模型。
• 虽然解析方法可以解决问题，但是求解过于复杂，此时计算机就可以提供简单可行的求解方法。
• 模型的灵敏度分析，希望在短时间内观察出系统的发展过程，以估计某些参数对系统的影响。
• 难以在实际环境中进行试验时，计算机时唯一的选择。
• 数据量过大，需要在大量方案中选优。
  计算机模拟是系统随时间变化的模拟。在通常情况下，系统数学模型可以根据时间划分为连续系统时间模型和离散系统时间模型。

  连续系统时间模型用实数表示时间，即系统可以在任意时刻点捕获其状态。状态取值通常是连续的连续，用常微分或偏微分方程表示；
  离散系统时间模型用整数表示时间，只在离散的时刻点上获取系统的状态。

  通过建模，得到系统数学模型后，就面临着系统数学模型的求解、分析、校验和验证、修正和应用等后处理。一般，计算机模拟过程是一个需要反复的过程，也只有通过不断的校验、验证，才能找到符合实际情况的高质量数学模型，找到计算准确高效的模型算法。

五、 生产与库存数量的方案问题选择

5.1 问题的提出

  某食品加工厂主要生产即食产品，一般当天生产的产品必须当天售出，否则就会出现不能保质、或变质、造成一定的经济损失，如果市场需求量大而生产量不足，则也会影响工厂的销售收入，该产品的单位成本为1.5元，单位产品售价为4元。工厂为了避免产品滞销存货过多而造成的经济损失，提出了如何制定合理的生产与库存数量的方案问题，能够使得工厂能有尽可能多的收益，经初步考虑拟从以下两种生产与库存方案中选出一个较好的方案：
  方案(1)：按前一天的销售量作为当天的生产库存量。
  方案(2)：按前两天的平均销售量作为当天的生产库存量。

5.2 解决问题的思路

  利用蒙特卡罗方法随机模拟市场对该产品需求量，统计计算出按照两种不同方案T 天后工厂的经济值，比较不同方案经济效益的大小，选出一个较好的方案。假设市场对该产品的每天需求数量是一个随机变量，从统计学的角度分析得知，该随机变量服从正态分布$N\left( 1500,30^2 \right) $

5.3 模型的建立与求解

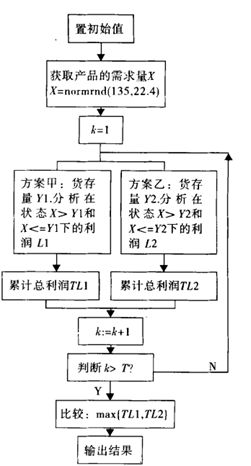
  根据上面的分析，利用蒙特卡罗方法编程实现，主要随机模拟前一天和前两天的各种不同的销售量，来确定当天的生产与库存量，依据可能的实际销售量，计算出当天的销售利润，选择使连续几天利润尽可能大的方案。
  流程图如下：

% 输入参数T,S1,S21,S22
% T: 模拟天数
% S1: 方案(1)前一天的销售量
% S21:方案(2)前第一天的销售量
% S22:方案(2)前第二天的销售量
% 返回 LS1,LS2:方案（1）利润；方案（2）利润
function [LS1,LS2]=code5(T,S1,S21,S22)
LS1 = 0; % 方案(1)实际累计总利润
LS2 = 0; % 方案(2)实际累计总利润
k = 1;
while k < T
KC1=S1; %KC1表示方案（1）当天的生产与库存量
KC2=(S21+S22)/2; %KC2表示方案（2）当天的生成与库存量
C=normrnd(1500,30*30); %生成正态分布随机数 C表示每天的需求量
if C

  这个MATLAB代码为一个函数function，需要我们先编写一个函数的.m文件，然后在命令行中输入相关参数即可返回结果。

  比如我假设模拟20天，方案一前一天的销售量为59，方案二前第一天的销售量为59，前第两天的销售量为65，那么我们在MATLAB的命令行中输入以下命令：

[LS1,LS2]=code5(20,59,59,65)

  得到的结果为

LS1 =7.9399e+04
LS2 =8.1732e+04

  比较可以发现，在假设的条件下，方案二的利润更高，因此选择方案二。

六、 连续系统模拟实例——四人同向行走问题

6.1 问题提出

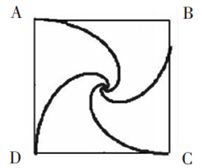
  如图所示，正方形ABCD的四个顶点各有一人.在某一时刻，四人同时出发以匀速$v=1$米/秒按顺时针方向追逐下一人，如果他们始终保持对准目标，则最终按螺旋状曲线交汇于中心点O，试求出这种情况下每个人的行进轨迹.

6.2 问题分析

  这是一道很经典的物理竞赛问题，本身来说并不难，再次只想考察蒙特卡洛模拟的理解。如果从理论分析来解决这个问题，可能需要大量的数学公式物理公式进行分析和计算，这是我们无法承受的，但是蒙特卡洛模拟可以将连续的系统转化为离散的系统。我们可以将每一时刻的人设为一个点，那么人连续的移动就可以离散出来。
##6.3 模型的建立与求解

1. 建立平面直角坐标系$A\left( x_1,y_1 \right) ,B\left( x_2,y_2 \right) ,C\left( x_3,y_3 \right) ,D\left( x_4,y_4 \right) $
2. 取时间间隔为$△t$，计算每一点在各个时刻的坐标。设某点在$t$时刻的坐标为$\left( x_i,y_i \right) $，则在$t+\bigtriangleup t$时刻的坐标为$\left( x_{\mathrm{i}}+v\Delta t\cos \alpha ,y_{\mathrm{i}}+v\Delta t\sin \alpha \right) $，其中
   $$\cos \alpha =\frac{x_{i+1}-x_{\mathrm{i}}}{d},\sin \alpha =\frac{y_{\mathrm{i}+1}-y_{\mathrm{i}}}{d}\text{，}d=\sqrt{{\left(x_{\mathrm{i}+1}-x_{\mathrm{i}}\right)}^2+{\left(y_{\mathrm{i}+1}-y_{\mathrm{i}}\right)}^2}$$
3. 取足够小的$\varepsilon $，$d<\varepsilon $时结束算法
4. 对每一个点，连接它在各时刻的位置，即得所求运动轨迹
   对应的MATLAB代码如下：

v=1;
dt=0.05;
x=[0 0 10 10];   % 设置初始坐标
y=[0 10 10 0];
for i=1:4
plot(x(i),y(i),'.'),hold on
end
d=20;
while(d>0.1)
x(5)=x(1);y(5)=y(1);
for i=1:4
d=sqrt((x(i+1)-x(i))^2+(y(i+1)-y(i))^2);
x(i)=x(i)+v*dt*(x(i+1)-x(i))/d;
y(i)=y(i)+v*dt*(y(i+1)-y(i))/d;
plot(x(i),y(i),'.'),hold on
end
end

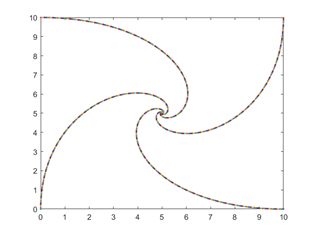
  运行后得到的结果如下：

6.4 模型的拓展

  这个模型可以拓展为正五边形的五个人行走，正六边形的六个人行走等等，蒙特卡洛模拟的优势就体现了出来，尽管再复杂，也能模拟出来。

七、 我关于蒙特卡洛模拟的看法

  在我看来，蒙特卡洛模拟不是一种算法，而是一种数学思维，类似于数形结合之类的。理论研究不出来，我就用计算机产生大量数据进行模拟，当然这个模拟不是随便模拟的，肯定要有很多的约束，是一种数学建模的思想，因此蒙特卡洛模拟就没有固定的算法或模板。

  最后想再次宣传一下我们的数学建模交流群

  公众号回复：数学建模，即可加入我们的群，我们一起交流资料，分享心得，互相答疑！

能力有限，如有错误，敬请指出

八、 参考文献

[1] 清风, 清风数学建模教程, B站链接https://www.bilibili.com/video/BV1DW411s7wi
[2] 陈红英. 数学建模与计算机解题[J]. 天水师范学院学报, 2006, 26(002):25-27.
[3] 欧宜贵, 李志林, 洪世煌. 计算机模拟在数学建模中的应用[J]. 海南大学学报:自然科学版, 2004, 022(001):89-95.
[4] 宋霄明. 计算机模拟在数学建模中的应用[J]. 数码世界, 2018, 000(004):132.
[5] 张仙风, 吕志鹏. 基于MATLAB的蒙特卡罗方法在可靠性设计中的应用[J]. 装备制造技术, 2006(04):82-83.