数学建模——人口预测模型
人口预测模型
- 多项式拟合
-
- 假设
- 特点
- 代码实现
-
- 代码实现思路
- 代码
- BP神经网络
-
- 特点
- 代码实现
-
- 实现思路
- 代码
- Logistic模型
-
- 特点
- 代码实现
-
- 原理
- 代码
多项式拟合
假设
- 把人口增长看做是一个多项式函数
- 人口增长没有限制,可以一直增长
特点
- 已有数据拟合的很好,不论数据有没有规律可言
- 预测未来一两年比较准确,越往后越不准确
- 预测的人口数量在未来会超出人口限制,且增长速度变快
代码实现
代码实现思路
以年份为x轴变量,当年人口为y轴变量,将两者进行拟合得到人口数模型与时间的关系式
,选取某城市2008到2019年老年人口数量进行模拟测试
代码
首先是将已有的数据拟合成一条曲线,过程代码如下所示
close
clc;
clear all %清除所有
n=5;%拟合多项式的次数
year=2008:2019;
num=[97.42 102.36 105.78 111.16 116.04 121.71 126.26 134.93 137 139 141.89 146];%户籍人口;
p5= polyfit(year,num,n); %5阶拟合
%绘制原始数据和拟合曲线图
figure(1)
hold on;
xlabel('year'); %设置横坐标名
ylabel('num'); %设置纵坐标名
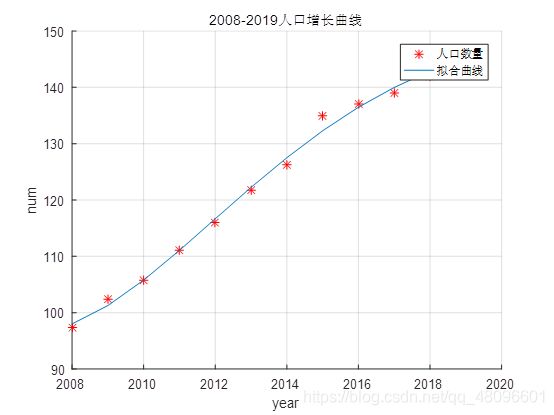
title('2008-2019人口增长曲线'); %设置标题
grid on %网格线
plot(year,num,'r*',year,polyval(p5,year))
legend('人口数量','拟合曲线')
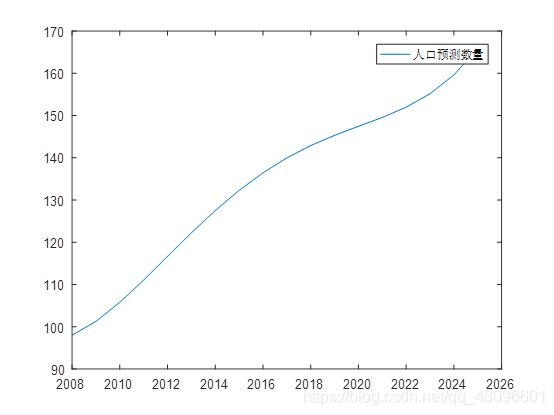
然后预测未来几年的人口增长数
figure(2)
year1=2008:2025;
plot(year1,polyval(p5,year1))
people=polyval(p5,year1);
legend('人口预测数量')
BP神经网络
特点
- BP神经网络预测人口模型不需要任何假设
- BP神经网络根据已有的数据推算数据内部之间的关系
- BP神经网络是非线性的方法
代码实现
实现思路
采用三层BP神经网络,利用已有数据推算出关系式,然后推算出下一年的人口,然后以下一年的人口为基础继续推算下下一年的人口
代码
clear all
close
clc
%原始数据
P=[97.42 102.36 105.78 111.16 116.04 121.71 126.26 134.93 137;
102.36 105.78 111.16 116.04 121.71 126.26 134.93 137 139;
105.78 111.16 116.04 121.71 126.26 134.93 137 139 141.89];
T=[111.16 116.04 121.71 126.26 134.93 137 139 141.89 146];
%归一化处理
[P,Pmin,Pmax,T,Tmin,Tmax]=premnmx(P,T);
%神经网络
net=newff(minmax(P),[5,1],{'tansig','purelin'});
net.trainFcn='trainbr';
%设置训练参数
net.trainParam.show=50;
net.trainParam.lr=0.05;
net.trainParam.epochs=500;
net.trainParam.goal=1e-5;
%训练
[net,tr]=train(net,P,T);
%仿真
A=sim(net,P);
a=postmnmx(A,Tmin,Tmax);
T=postmnmx(T,Tmin,Tmax);
%优化后输入层权值和阙值
inputWeights=net.IW{1,1};
inputbias=net.b{1};
%优化后网络层权值和阙值
layerWeights=net.LW{2,1};
layerbias=net.b{2};
%画图输出
x=2011:2019;
newk=a(1,:);
figure(1)
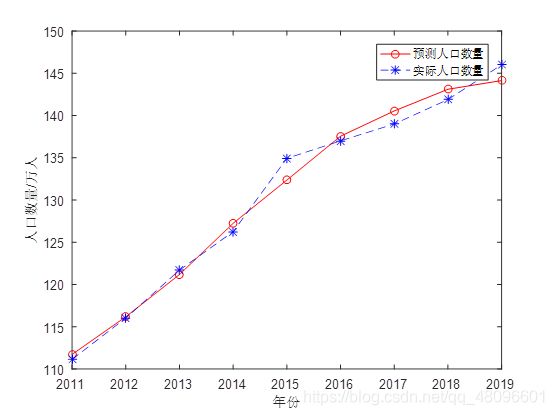
plot(x,newk,'r-o',x,T,'b--*')
xlabel('年份')
ylabel('人口数量/万人')
legend('预测人口数量','实际人口数量')
Pnew=[139;141.89;146];
OldNum=zeros(15,1);
for i=1:15
SamNum=size(Pnew,2);
Pnewn=tramnmx(Pnew,Pmin,Pmax);
HiddenOut=tansig(inputWeights*Pnewn+repmat(inputbias,1,SamNum));
anewn=purelin(layerWeights*HiddenOut+repmat(layerbias,1,SamNum));
anewn=postmnmx(anewn,Tmin,Tmax);
Pnew(1:3,:)=[Pnew(2:3,:);anewn];
OldNum(i)=anewn;
end
%画图输出
x1=2011:2034;
figure(2)
NUM=[newk,OldNum'];
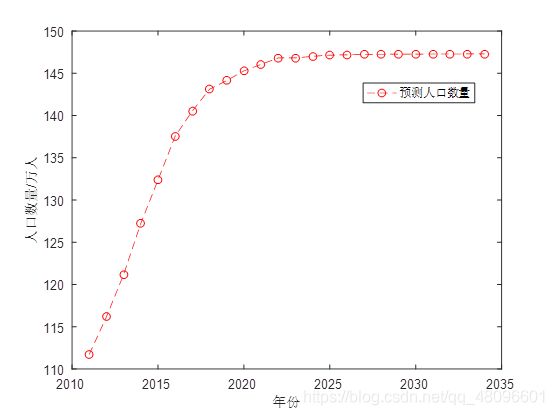
plot(x1,NUM,'r--o')
xlabel('年份')
ylabel('人口数量/万人')
legend('预测人口数量')
Logistic模型
特点
- 考虑了人口能够承受的最大值
- 数据出错时拟合的不够好,必须要有正确的数据才能够拟合
- 数学模型简单,有一定的公式
代码实现
原理
Logistic模型认为人口增长有最大值Xm和人口的固有增长率r0。当人口增长到Xm附近,人口将保持这个水准不会有大的变动,数学公式如下
dx/dt=r0(1-x/Xm)x
x(0)=x0
x是人口数量,x0是初始人口数量
解这个方程组得到
x=Xm/(1+(Xm/x0-1)exp(-r0t))
代码
clc
clear
close all
x=[97.42 102.36 105.78 111.16 116.04 121.71 126.26 134.93 141.24 141.89 143.2 147];%常驻老年人口
n=length(x);
t=0:1:n-1;
rk=zeros(1,n);
rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
for i=2:n-1
rk(i)=(x(i+1)-x(i-1))/2;
end
rk=rk./x;
p=polyfit(x,rk,1);
b=p(2);
a=p(1);
r0=b;
xm=-r0/a;
%输出
pnum=zeros(n,1);
for i=0:1:n-1
pnum(i+1)=xm/(1+(xm/x(1)-1)*exp(-r0*i));
end
year1=2008:2019;
plot(year1,pnum,'r--o',year1,x,'k-*')
xlabel('年份')
ylabel('老年人口数量/万人')
legend('预测老年人口数量','实际老年人口数量')
figure(2)
fnum=zeros(n+16,1);
for i=0:1:n+15
fnum(i+1)=xm/(1+(xm/x(1)-1)*exp(-r0*i));
end
year2=2008:2035;
plot(year2,fnum,'r--o')
xlabel('年份')
ylabel('老年人口数量/万人')
legend('预测老年人口数量')