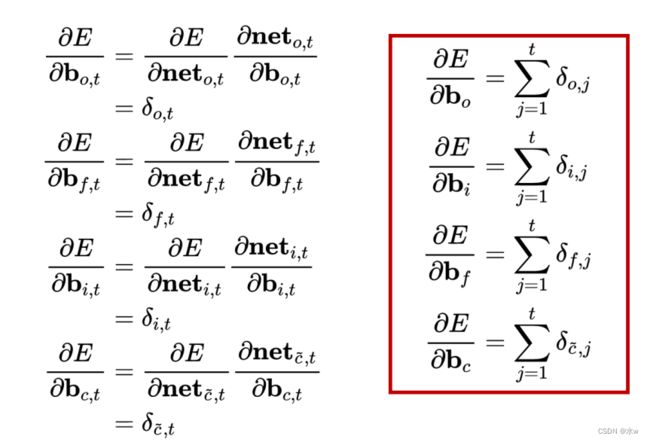深度学习之 12 循环神经网络RNN2

本文是接着上一篇深度学习之 12 循环神经网络RNN_水w的博客-CSDN博客

目录

回顾

1 长程依赖问题

◼   为什么在实际应用中，RNN很难处理长距离的依赖？

◼  梯度消失举例

◼  三种方法应对梯度消失问题

◼  sigmoid函数与tanh函数比较：

◼  更加推荐：ReLU函数的图像和导数图

 2 长短期记忆网络（LSTM）

◼  LSTM使用三个控制开关

◼  LSTM 的重复模块

 ◼  LSTM 的核心思想

◼  “门”（gate）

◼  逐步理解 LSTM之遗忘门

◼  逐步理解 LSTM之输入门

◼  逐步理解 LSTM之更新单元状态

◼  逐步理解 LSTM之输出门

（1） LSTM训练算法框架

（2）关于公式和符号的说明

（3）误差项沿时间的反向传递

（4）将误差项传递到上一层

（5）权重梯度的计算

 3 门控循环神经网络（GRU）

◼  优点

◼  LSTM与GRU

4 深层循环神经网络

◼  堆叠循环神经网络 (Stacked Recurrent Neural Network, SRNN)

◼  双向循环神经网络(Bidirectional Recurrent Neural Network)

---

回顾

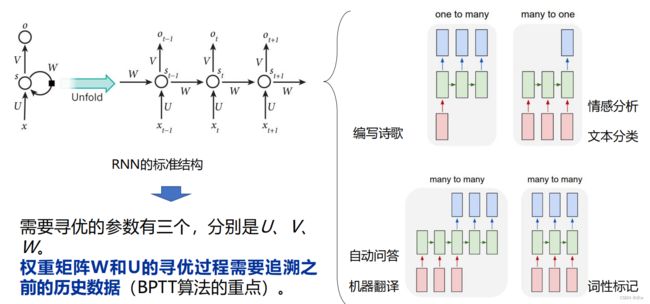
需要寻优的参数有三个，分别是 U、V、W 。

权重矩阵W和U的寻优过程需要追溯之 前的历史数据 （BPTT算法的重点）。

1 长程依赖问题

RNN 的长处之一是它可以利用先前的信息到当前的任务上，尤其当相关的信息和预测的词之间的间隔较小时效果明显。

如预测句子“the clouds are in the sky ”中的最后一个词。

 然而在间隔不断增大时，RNN 会丧失学习到连接如此远的信息的能力。

如预测句子“I grew up in France… I speak fluent French ”中最后一个词。

◼   为什么在实际应用中，RNN很难处理长距离的依赖？

上一节关于RNN的推导中，误差项 沿时间 反向传播的公式为：

 根据下面的不等式，来获取的模的上界（模可以看做对 中每一项值的大小的度量）:

 其中，、分别是对角矩阵和矩阵W模的上界。

可以看到，误差项从 时刻传递到 时刻，其值的上界是 的 指数函数 。

当 − 很大时(也就是误差传递很多个时刻时), 整个式子的值就会变得极小(当 乘积小于1)或者极大(当 乘积大于1)，前者是 梯度消失 ，后者是 梯度爆炸 。

梯度消失或者梯度爆炸会导致梯度为0或NaN，没法继续训练更新参数，也就是RNN的长程依赖问题 。

◼  梯度消失举例

RNN中权重矩阵W最终的梯度是 各个时刻的梯度之和 ，即：

 假设某轮训练中，各时刻的梯度以及最终的梯度之和如下图：

 从t-3时刻开始，梯度已经几乎减少到0了。即从此时刻开始再往之前走，得到的梯度（几乎为零）就不会对最终的梯度值有任何贡献。这就是原始RNN无法处理长距离依赖的原因。

◼  三种方法应对梯度消失问题

通常来说， 梯度爆炸 更容易处理一些。因为梯度爆炸的时候，程序会收到 NaN 错误。也可以设置一个梯度阈值，当梯度超过这个阈值时直接截取。

梯度消失 更难检测，也更难处理一些。总的来说，有三种方法应对梯度消失问题：

1. 合理的初始化权重值。 初始化权重，使每个神经元尽可能不要取极大或极小

值，以躲开梯度消失的区域。

2. 使用relu代替sigmoid和tanh作为激活函数。

3. 使用其他结构的RNNs ，比如长短时记忆网络（LTSM）和门控循环神经网络Gated Recurrent Unit（GRU）。

接下来将重点介绍LSTM和GRU两种网络。

◼  sigmoid函数与tanh函数比较：

• sigmoid函数的导数值范围为 (0,0.25] ，反向传播时会导致梯度消失

• tanh函数的导数值范围为 (0,1] ，相对范围较大，但仍会导致梯度消失

• sigmoid函数不是原点中心对称，输出均大于0

• tanh函数是原点中心对称，可以使网络收敛的更好

sigmoid函数的函数图和导数图：

 虽然tanh函数相较于sigmoid函数而言比较相似，但是tanh函数的导函数（0~1）比sigmoid函数的导函数（0~1/4）大，tanh函数的函数图和导数图：

◼  更加推荐：ReLU函数的图像和导数图

ReLU函数的左侧导数为0，右侧导数恒为1，避免了小数的连乘，但反向传播中仍有权值的累乘。ReLU函数 改善 了“梯度消失”现象。

非常借鉴了人体神经元的单边抑制单边激活，ReLU函数的图像和导数图：

 缺陷：左侧基本为0，容易使得神经元就直接学死了，所以基本上会使用ReLU函数的变体。

 2 长短期记忆网络（LSTM）

Long Short Term Memory networks（以下简称 LSTMs ），一种特殊的RNN网络，该网络设计出来是为了解决长程依赖问题。

增加状态c，称为单元状态(cell state)，让它来保存长期的状态

 LSTMs首先继承了RNN模型的特性，所以它是具有短期记忆功能的。 其次，它的特殊的记忆单元的设置，也让它具备了长期记忆的功能。

◼  LSTM使用三个控制开关

 LSTM通过所谓的开关设置，去实现我们的这样一个状态单元C以及隐藏层的输出，那么我们下面来看一下这三个非常重要的状态单元是什么。

LSTM的关键，就是怎样控制长期状态 c 。LSTM使用三个控制开关 ：

        ① 第 一 个开关，负责控制如何继续保存长期状态 c

        ② 第 二 个开关，负责控制把即时状态输入到长期状态 c ；

        ③ 第 三 个开关，负责控制是否把长期状态 c 作为当前的LSTM的输出；

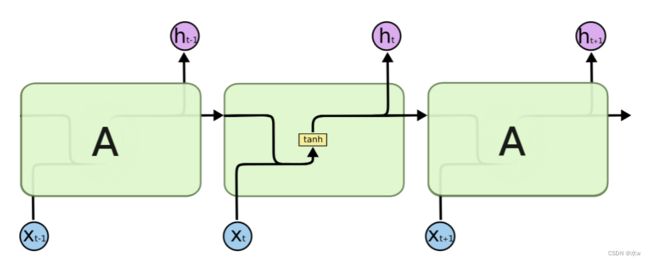
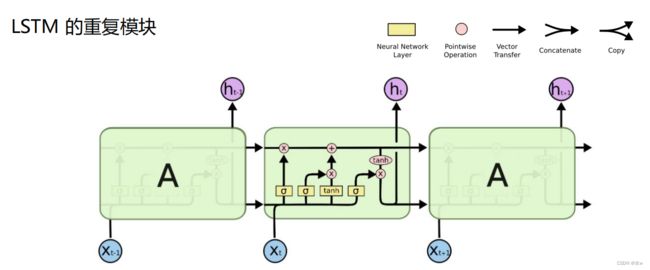
◼  LSTM 的重复模块

每一个模块表示的是不同的时刻。

标准RNN的重复模块如下，其中某一个时刻里面其实就这样一个tanh激活函数这么一个过程，相对来说内部结构比较简单。

而LSTM 的重复模块如下，除了h在随时间流动，单元状态c也在随时间流动，单元状态c就代表着长期记忆。

• 黄框：表示我们学习得到的神经网络层；
• 粉色圆：表示的是一些运算操作；
• 单箭头：箭头流向表示向量传输的方向；
• 两个箭头合并：表示向量的一个拼接过程；
• 箭头分叉：表示向量的复制过程；

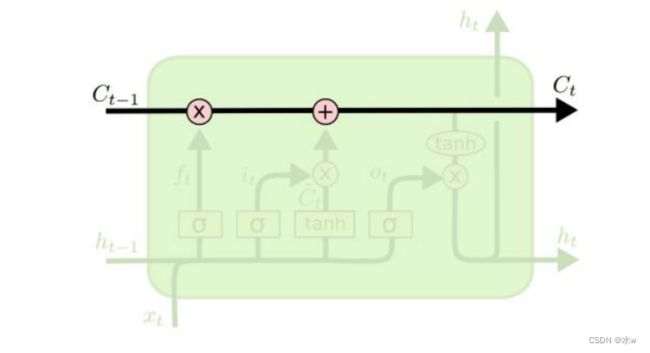
 ◼  LSTM 的核心思想

与RNN很大一个区别：LSTM 的关键是状态单元C，如水平线在图上方贯穿运行。

单元状态的传递类似于传送带，其直接在整个链上运行，中间只有一些少量的线性交互，容易保存相关信息。

◼  “门”（gate）

前面描述的开关是怎样在算法中实现的呢？

LSTM 通过精心设计的称作为 “门”（gate） 的结构来去除或者增加单元状态中的信息。门是一种让信息选择式通过的方法。

 此门包含一个 sigmoid 神经网络层和一个 pointwise 乘法操作。

补充： LSTM用两个门来控制单元状态c的内容 ：

        ➢ 遗忘门（forget gate） ，它决定了上一时刻的单元状态 c t-1 有多少保留到 当前时刻 c t （有多少会被记住） ；

        ➢ 输入门（input gate） ，它决定了当前时刻网络的输入 x t 有多少保存到单 元状态 c t 。

                • LSTM用输出门 来控制单元状态 c t 有多少输出到 LSTM的当前输出值 h t

◼  逐步理解 LSTM之遗忘门

这个门怎么做到“遗忘“的呢？怎么理解？既然是遗忘旧的内容，为什么这个门还要接收新的?  

用人来举例，我们脑海中记住了很多知识，但是知识不用的时候，我们是想不起来的。

假设现在出一道题去考你，你就会对其相关的知识进行回忆，那么这个回忆的过程就会有意识地去遗忘一些内容，记住一些内容，那在这个里面，为什么有些被记住了，有些被遗忘了？

其实就是这个新刺激Xt做了一个选择，或者说做了一个鞭策，去决定哪些是需要被遗忘的，哪些是需要被记住的。当然这个记住和遗忘的比例是多少，那么我们用通过S得到一个0~1的值去进行一个权衡选择。

◼  逐步理解 LSTM之输入门

sigmoid 函数称 为输入门，决定将要更新什么值 ；

tanh 层创建一个新的候选值向量， 会被加入到状态中；

◼  逐步理解 LSTM之更新单元状态

由于遗忘门的控制，它可以保存很久很久之前的信息，

由于输入门的控制，它又可以避免当前无关紧要的内容进入记忆。

◼  逐步理解 LSTM之输出门

输出门控制了长期记忆对当前输出的影响，其由输出门和单元状态共同确定。

（1） LSTM训练算法框架 

• 遗忘门：公式1
• 输入门：公式2和公式3，公式4（当前状态单元Ct的一个更新过程）
• 输出门：公式5和公式6

 LSTM的训练算法仍然是反向传播算法。主要有下面三个步骤：

        ① 前向计算每个神经元的输出值，对于LSTM来说，即五个 向量的值。计算方法已经在上一页中描述过了。

        ② 反向计算每个神经元的误差项 值。与 循环神经网络 一样，LSTM误差项的反向传播也是包括两个方向： 一个是沿时间的反向传播 ，即从当前t时刻 开始，计算每个时刻的误差项； 一个是将误差项向上一层传播 。

        ③ 根据相应的误差项，计算每个权重的梯度。

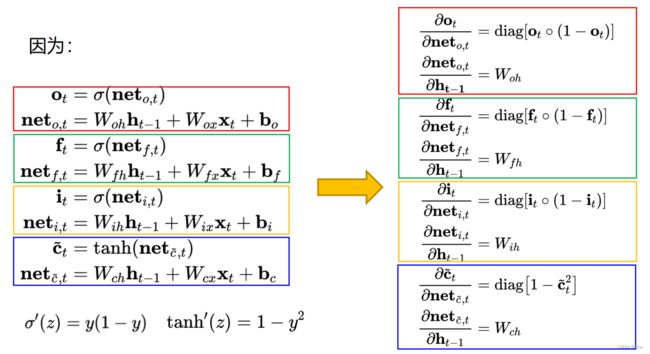
（2）关于公式和符号的说明

设定门gate的激活函数为 sigmoid函数 ，输出的激活函数为 tanh函数 。它们的导数分别为：

 sigmoid和tanh函数的导数都是原函数的函数。这样，一旦计算原函数的值，就可以用它来计算出导数的值。

LSTM需要学习的参数共有8组，分别是：

• 遗忘门的权重矩阵和偏置项 、
• 输入门的权重矩阵和偏置项 、
• 输出门的权重矩阵 和偏置项 、
• 计算单元状态的权重矩阵和偏置项 。

因为权重矩阵的两部分在反向传播中使用不同的公式，因此在后续的推导中，权重矩阵 都将被写为分开的两个矩阵:

 

当O作用于两个 矩阵 时，两个矩阵对应位置的元素相乘。按元素乘可以在某些情况下简化矩阵

和向量运算。例如，当一个对角矩阵右乘一个矩阵时，相当于用对角矩阵的对角线组成的向量

按元素乘那个矩阵：

 当一个行向量右乘一个对角矩阵时，相当于这个行向量按元素乘那个矩阵对角线组成的向量：

 上面这两点，在后续推导中会多次用到。

（3）误差项沿时间的反向传递

上述公式就是将误差沿时间反向传播一个时刻的公式。有了它，可以写出将误差项向前传递到任意时刻的公式：

（4）将误差项传递到上一层

（5）权重梯度的计算

对于 的权重梯度，我们知道它的 梯度是各个时刻梯度之和 ， 我们首先求出它们在t时刻的 梯度，然后再求出他们最终的梯度。

对于偏置项bf,bi,bc,bo的梯度，也是将 各个时刻的梯度加在一起 。下面是各个时刻的偏 置项梯度：

对于 的权重梯度， 只需要根据相应的误差项直接计算即可

 

 3 门控循环神经网络（GRU）

GRU（Gate Recurrent Unit）是循环神经网络RNN的一种。和LSTM一样，也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。

◼  优点

GRU是LSTM的一种变体，它较LSTM网络的结构更加简单，而且效果也很好。

LSTM引入了三个门函数： 输入门 、 遗忘门 和 输出门 来控制输入值、记忆值和输出值。而在GRU模型中只有两个门，分别是 更新门和重置门 。 另外，GRU将单元状态与输出合并为一个状态h。

 

◼  LSTM与GRU

• GRU的参数更少，因而训练稍快或需要更少的数据来泛化。

• 如果你有足够的数据，LSTM的强大表达能力可能会产生更好的结果。

Greff, et al. (2016)对流行的LSTM变种做了对比实验，发现它们的表现几乎一致。 Jozefowicz, et al. (2015)测试了超过一万中RNN结构，发现某些任务情形下，有 些变种比LSTM工作得更好。

4 深层循环神经网络

⚫ 循环神经网络是可深可浅的网络

        ➢ 深网络：把循环网络按时间展开，长时间间隔的状态之间的路径很长 ；

        ➢ 浅网络：同一时刻网络输入到输出之间的路径 x t → y t 非常浅 ；

⚫ 增加循环神经网络的深度的意义

        ➢ 增强循环神经网络的能力 ；

        ➢ 增加同一时刻网络输入到输出之间的路径 x t → y t , 如增加隐状态到输出 h t → y t ，以及输入到隐状态 x t → h t 之间的路径的深度；

◼  堆叠循环神经网络 (Stacked Recurrent Neural Network, SRNN)

◼  双向循环神经网络(Bidirectional Recurrent Neural Network)

双向循环神经网络(Bidirectional Recurrent Neural Network)由两层循环神经网络组成，它们的输入相同，只是信息传递的方向不同