POJ 3155 Hard Life
Hard Life
64-bit integer IO format: %lld Java class name: Main
John is a Chief Executive Officer at a privately owned medium size company. The owner of the company has decided to make his son Scott a manager in the company. John fears that the owner will ultimately give CEO position to Scott if he does well on his new manager position, so he decided to make Scott’s life as hard as possible by carefully selecting the team he is going to manage in the company.
John knows which pairs of his people work poorly in the same team. John introduced a hardness factor of a team — it is a number of pairs of people from this team who work poorly in the same team divided by the total number of people in the team. The larger is the hardness factor, the harder is this team to manage. John wants to find a group of people in the company that are hardest to manage and make it Scott’s team. Please, help him.
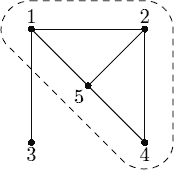
In the example on the picture the hardest team consists of people 1, 2, 4, and 5. Among 4 of them 5 pairs work poorly in the same team, thus hardness factor is equal to 5⁄4. If we add person number 3 to the team then hardness factor decreases to 6⁄5.
Input
The first line of the input file contains two integer numbers n and m (1 ≤ n ≤ 100, 0 ≤ m ≤ 1000). Here n is a total number of people in the company (people are numbered from 1 to n), and m is the number of pairs of people who work poorly in the same team. Next m lines describe those pairs with two integer numbers ai and bi (1 ≤ ai, bi ≤ n, ai ≠ bi) on a line. The order of people in a pair is arbitrary and no pair is listed twice.
Output
Write to the output file an integer number k (1 ≤ k ≤ n) — the number of people in the hardest team, followed by k lines listing people from this team in ascending order. If there are multiple teams with the same hardness factor then write any one.
Sample Input
sample input #1 5 6 1 5 5 4 4 2 2 5 1 2 3 1 sample input #2 4 0
Sample Output
sample output #1 4 1 2 4 5 sample output #2 1 1
Source

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cmath> 5 #include <algorithm> 6 #include <climits> 7 #include <vector> 8 #include <queue> 9 #include <cstdlib> 10 #include <string> 11 #include <set> 12 #include <stack> 13 #define LL long long 14 #define pii pair<int,int> 15 #define INF 0x3f3f3f3f 16 using namespace std; 17 const int maxn = 1200; 18 struct arc{ 19 int to,next; 20 double flow; 21 arc(int x = 0,double y = 0,int z = -1){ 22 to = x; 23 flow = y; 24 next = z; 25 } 26 }; 27 arc e[maxn<<3]; 28 int head[maxn],d[maxn],cur[maxn],x[maxn],y[maxn]; 29 int tot,S,T,n,m; 30 void add(int u,int v,double flow){ 31 e[tot] = arc(v,flow,head[u]); 32 head[u] = tot++; 33 e[tot] = arc(u,0,head[v]); 34 head[v] = tot++; 35 } 36 bool bfs(){ 37 memset(d,-1,sizeof(d)); 38 queue<int>q; 39 q.push(S); 40 d[S] = 1; 41 while(!q.empty()){ 42 int u = q.front(); 43 q.pop(); 44 for(int i = head[u]; ~i; i = e[i].next){ 45 if(e[i].flow > 0&& d[e[i].to] == -1){ 46 d[e[i].to] = d[u] + 1; 47 q.push(e[i].to); 48 } 49 } 50 } 51 return d[T] > -1; 52 } 53 double dfs(int u,double low){ 54 if(u == T) return low; 55 double tmp = 0,a; 56 for(int &i = cur[u]; ~i; i = e[i].next){ 57 if(e[i].flow>0&&d[e[i].to] == d[u]+1 && (a=dfs(e[i].to,min(e[i].flow,low))) > 0){ 58 e[i].flow -= a; 59 e[i^1].flow += a; 60 low -= a; 61 tmp += a; 62 if(low <= 0) break; 63 } 64 } 65 if(tmp <= 0) d[u] = -1; 66 return tmp; 67 } 68 bool dinic(){ 69 double flow = m; 70 while(bfs()){ 71 memcpy(cur,head,sizeof(head)); 72 double tmp = dfs(S,INF); 73 if(tmp > 0) flow -= tmp; 74 } 75 return flow <= 0; 76 } 77 void build(double delta){ 78 memset(head,-1,sizeof(head)); 79 tot = 0; 80 for(int i = 1; i <= m; ++i){ 81 add(S,i+n,1.0); 82 add(i+n,x[i],INF); 83 add(i+n,y[i],INF); 84 } 85 for(int i = 1; i <= n; ++i) add(i,T,delta); 86 } 87 int main() { 88 while(~scanf("%d %d",&n,&m)){ 89 S = 0; 90 T = n + m + 1; 91 for(int i = 1; i <= m; ++i) 92 scanf("%d %d",x+i,y+i); 93 if(m == 0) printf("1\n1\n"); 94 else{ 95 double low = 0,high = 1.0*m,mid; 96 const double exps = 1.0/(n*n); 97 while(high - low >= exps){ 98 mid = (low + high)/2.0; 99 build(mid); 100 if(dinic()) high = mid; 101 else low = mid; 102 } 103 build(low); 104 dinic(); 105 int cnt = 0,ans[maxn]; 106 for(int i = 1; i <= n; ++i) 107 if(d[i] > 1) ans[cnt++] = i; 108 printf("%d\n",cnt); 109 for(int i = 0; i < cnt; ++i) 110 printf("%d%c",ans[i],'\n'); 111 } 112 } 113 return 0; 114 }
第二种建模方案

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cmath> 5 #include <algorithm> 6 #include <climits> 7 #include <vector> 8 #include <queue> 9 #include <cstdlib> 10 #include <string> 11 #include <set> 12 #include <stack> 13 #define LL long long 14 #define pii pair<int,int> 15 #define INF 0x3f3f3f3f 16 using namespace std; 17 const int maxn = 200; 18 struct arc{ 19 int to,next; 20 double flow; 21 arc(int x = 0,double y = 0,int z = -1){ 22 to = x; 23 flow = y; 24 next = z; 25 } 26 }; 27 arc e[maxn*maxn]; 28 int head[maxn],cur[maxn],d[maxn],du[maxn]; 29 int tot,S,T,n,m,cnt; 30 pii p[maxn*maxn]; 31 void add(int u,int v,double flow){ 32 e[tot] = arc(v,flow,head[u]); 33 head[u] = tot++; 34 e[tot] = arc(u,0,head[v]); 35 head[v] = tot++; 36 } 37 bool bfs(){ 38 memset(d,-1,sizeof(d)); 39 d[S] = 1; 40 queue<int>q; 41 q.push(S); 42 cnt = 0; 43 while(!q.empty()){ 44 int u = q.front(); 45 q.pop(); 46 for(int i = head[u]; ~i; i = e[i].next){ 47 if(e[i].flow > 0 && d[e[i].to] == -1){ 48 d[e[i].to] = d[u] + 1; 49 q.push(e[i].to); 50 cnt++; 51 } 52 } 53 } 54 return d[T] > -1; 55 } 56 double dfs(int u,double low){ 57 if(u == T) return low; 58 double tmp = 0,a; 59 for(int &i = cur[u]; ~i; i = e[i].next){ 60 if(e[i].flow > 0 && d[u] + 1 == d[e[i].to]&&(a=dfs(e[i].to,min(e[i].flow,low)))>0){ 61 e[i].flow -= a; 62 e[i^1].flow += a; 63 low -= a; 64 tmp += a; 65 if(low <= 0) break; 66 } 67 } 68 if(tmp <= 0) d[u] = -1; 69 return tmp; 70 } 71 bool dinic(){ 72 double ans = n*m; 73 while(bfs()){ 74 memcpy(cur,head,sizeof(head)); 75 ans -= dfs(S,INF); 76 } 77 return ans/2.0 > 0; 78 } 79 void build(double g){ 80 memset(head,-1,sizeof(head)); 81 for(int i = tot = 0; i < m; ++i){ 82 add(p[i].first,p[i].second,1); 83 add(p[i].second,p[i].first,1); 84 } 85 for(int i = 1; i <= n; ++i){ 86 add(S,i,m); 87 add(i,T,m+g*2.0-du[i]); 88 } 89 } 90 int main() { 91 while(~scanf("%d %d",&n,&m)){ 92 S = 0; 93 T = n + 1; 94 memset(du,0,sizeof(du)); 95 for(int i = 0; i < m; ++i){ 96 scanf("%d %d",&p[i].first,&p[i].second); 97 ++du[p[i].first]; 98 ++du[p[i].second]; 99 } 100 if(!m) printf("1\n1\n"); 101 else{ 102 const double exps = 1.0/(n*n); 103 double low = 0,high = m; 104 while(high - low >= exps){ 105 double mid = (low + high)/2.0; 106 build(mid); 107 if(dinic()) low = mid; 108 else high = mid; 109 } 110 build(low); 111 dinic(); 112 printf("%d\n",cnt); 113 for(int i = 1; i <= n; ++i) 114 if(d[i] > -1) printf("%d\n",i); 115 } 116 } 117 return 0; 118 }
