Matlab算法模版(一)——模拟退火和灰色预测
模拟退火和灰色预测
- 一、模拟退火matlab算法模板
- 二、灰色预测matlab算法模板
一、模拟退火matlab算法模板
模拟退火解决TSP问题:
- 计算两两城市之间的距离
function D=Distanse(a)
%输入 a 各城市的位置坐标
%输出 D 两两城市之间的距离
row=size(a,1);% 返回的是矩阵a所对应的行数(1对应的是行数,2对应的是列数)
D=zeros(row,row);% 返回一个rowxrow的零矩阵
for i=1:row
for j=i+1:row
D(i,j)=((a(i,1)-a(j,1))^2+(a(i,2)-a(j,2))^2)^0.5;
D(j,i)=D(i,j);
end
end
- 画路径函数
% 输入
% Chrom 待画路径
% X 各城市坐标位置
R=[Chrom(1,:) Chrom(1,1)]; %一个随机解(个体)
figure; % 显示多个窗口
hold on % 把轨迹图添加在折线图上面
plot(X(:,1),X(:,2),'o','color',[0.5,0.5,0.5])
plot(X(Chrom(1,1),1),X(Chrom(1,1),2),'rv','MarkerSize',20)
for i=1:size(X,1) % size(X,1) % 返回矩阵X的行数
text(X(i,1)+0.05,X(i,2)+0.05,num2str(i),'color',[1,0,0]);
end
A=X(R,:); % 将矩阵x的第R行赋给y(冒号右边是列)
row=size(A,1);
for i=2:row
[arrowx,arrowy] = dsxy2figxy(gca,A(i-1:i,1),A(i-1:i,2));%坐标转换
annotation('textarrow',arrowx,arrowy,'HeadWidth',8,'color',[0,0,1]);
end
hold off % 恢复为默认状况,plot后将取代旧的figure
代码:
xlabel('横坐标')
ylabel('纵坐标')
title('轨迹图')
box on % 显示坐标区轮廓
- dsxy2figxy
function varargout = dsxy2figxy(varargin)
if length(varargin{1}) == 1 && ishandle(varargin{1}) ...
&& strcmp(get(varargin{1},'type'),'axes')
hAx = varargin{1};
varargin = varargin(2:end);
else
hAx = gca;
end;
if length(varargin) == 1
pos = varargin{1};
else
[x,y] = deal(varargin{:});
end
axun = get(hAx,'Units');
set(hAx,'Units','normalized');
axpos = get(hAx,'Position');
axlim = axis(hAx);
axwidth = diff(axlim(1:2));
axheight = diff(axlim(3:4));
if exist('x','var')
varargout{1} = (x - axlim(1)) * axpos(3) / axwidth + axpos(1);
varargout{2} = (y - axlim(3)) * axpos(4) / axheight + axpos(2);
else
pos(1) = (pos(1) - axlim(1)) / axwidth * axpos(3) + axpos(1);
pos(2) = (pos(2) - axlim(3)) / axheight * axpos(4) + axpos(2);
pos(3) = pos(3) * axpos(3) / axwidth;
pos(4) = pos(4) * axpos(4 )/ axheight;
varargout{1} = pos;
end
set(hAx,'Units',axun)
- 当前解和路线距离
function [S,R]=Metropolis(S1,S2,D,T)
%% 输入
% S1: 当前解
% S2: 新解
% D: 距离矩阵(两两城市的之间的距离)
% T: 当前温度
%% 输出
% S: 下一个当前解
% R: 下一个当前解的路线距离
%%
R1=PathLength(D,S1); %计算路线长度
N=length(S1); %得到城市的个数
R2=PathLength(D,S2); %计算路线长度
dC=R2-R1; %计算能力之差
if dC<0 %如果能力降低 接受新路线
S=S2;
R=R2;
elseif exp(-dC/T)>=rand %以exp(-dC/T)概率接受新路线
S=S2;
R=R2;
else %不接受新路线
S=S1;
R=R1;
end
- 新解s2
function S2=NewAnswer(S1)
%% 输入
% S1:当前解
%% 输出
% S2:新解
N=length(S1); % 长度
S2=S1;
a=round(rand(1,2)*(N-1)+1); %产生两个随机位置 用来交换
W=S2(a(1));
S2(a(1))=S2(a(2));
S2(a(2))=W; %得到一个新路线
- 输出路径函数
function p=OutputPath(R)
%% 输出路径函数
%输入:R 路径
R=[R,R(1)];
N=length(R);
p=num2str(R(1));% 把数值转换成字符串, 转换后可以使用disp函数进行输出。
for i=2:N
p=[p,'—>',num2str(R(i))];
end
disp(p)
- 计算各个体的路径长度
function len=PathLength(D,Chrom)
%% 计算各个体的路径长度
% 输入:
% D 两两城市之间的距离
% Chrom 个体的轨迹
[row,col]=size(D);
NIND=size(Chrom,1);
len=zeros(NIND,1);
for i=1:NIND
p=[Chrom(i,:) Chrom(i,1)];
i1=p(1:end-1);
i2=p(2:end);
len(i,1)=sum(D((i1-1)*col+i2)); # 求和
end
- SA_TSP
clc;
clear;
close all;
warning off;
%%
tic
T0=1000; % 初始温度
Tend=1e-3; % 终止温度
L=200; % 各温度下的迭代次数(链长)
q=0.9; %降温速率
X=[16.4700 96.1000
16.4700 94.4400
20.0900 92.5400
22.3900 93.3700
25.2300 97.2400
22.0000 96.0500
20.4700 97.0200
17.2000 96.2900
16.3000 97.3800
14.0500 98.1200
16.5300 97.3800
21.5200 95.5900
19.4100 97.1300
20.0900 92.5500];
%%
D=Distanse(X); %计算距离矩阵
N=size(D,1); %城市的个数
%% 初始解
S1=randperm(N); %随机产生一个初始路线
%% 画出随机解的路径图
DrawPath(S1,X)
pause(0.0001)
%% 输出随机解的路径和总距离
disp('初始种群中的一个随机值:')
OutputPath(S1);
Rlength=PathLength(D,S1);
disp(['总距离:',num2str(Rlength)]);
%% 计算迭代的次数Time
% Time=ceil(double(solve(['1000*(0.9)^x=',num2str(Tend)])));
syms x;
eq = 1000*(0.9)^x == num2str(Tend);
Time=ceil(double(solve(eq,x)));
count=0; %迭代计数
Obj=zeros(Time,1); %目标值矩阵初始化
track=zeros(Time,N); %每代的最优路线矩阵初始化
%% 迭代
while T0>Tend
count=count+1; %更新迭代次数
temp=zeros(L,N+1);
for k=1:L
%% 产生新解
S2=NewAnswer(S1);
%% Metropolis法则判断是否接受新解
[S1,R]=Metropolis(S1,S2,D,T0); %Metropolis 抽样算法
temp(k,:)=[S1 R]; %记录下一路线的及其路程
end
%% 记录每次迭代过程的最优路线
[d0,index]=min(temp(:,end)); %找出当前温度下最优路线
if count==1 || d0<Obj(count-1)
Obj(count)=d0; %如果当前温度下最优路程小于上一路程则记录当前路程
else
Obj(count)=Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程
end
track(count,:)=temp(index,1:end-1); %记录当前温度的最优路线
T0=q*T0; %降温
fprintf('经过%d代,最优路径距离为:%f\n',count,Obj(count)) %输出当前迭代次数
end
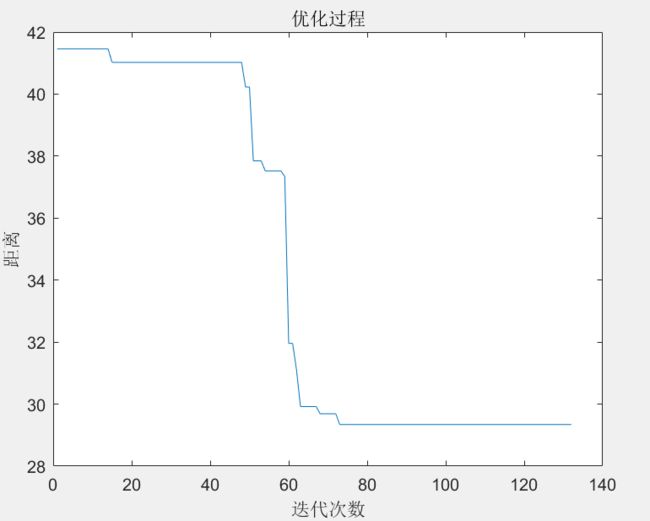
%% 优化过程迭代图
figure
plot(1:count,Obj)
xlabel('迭代次数')
ylabel('距离')
title('优化过程')
%% 最优解的路径图
DrawPath(track(end,:),X)
%% 输出最优解的路线和总距离
disp('最优解:')
S=track(end,:);
p=OutputPath(S);
disp(['总距离:',num2str(PathLength(D,S))]);
disp('-------------------------------------------------------------')
toc
初始种群中的一个随机值:
9—>7—>2—>12—>10—>11—>3—>14—>5—>8—>1—>13—>6—>4—>9
总距离:62.3375
经过1代,最优路径距离为:49.524654
经过2代,最优路径距离为:47.949766
经过3代,最优路径距离为:47.949766
经过4代,最优路径距离为:47.949766
经过5代,最优路径距离为:47.949766
经过6代,最优路径距离为:47.949766
经过7代,最优路径距离为:47.949766
经过8代,最优路径距离为:46.577563
经过9代,最优路径距离为:46.577563
经过10代,最优路径距离为:43.263988
经过11代,最优路径距离为:39.867984
经过12代,最优路径距离为:39.867984
经过13代,最优路径距离为:39.867984
经过14代,最优路径距离为:39.867984
经过15代,最优路径距离为:39.867984
经过16代,最优路径距离为:39.867984
经过17代,最优路径距离为:39.867984
经过18代,最优路径距离为:39.867984
经过19代,最优路径距离为:39.867984
经过20代,最优路径距离为:39.867984
经过21代,最优路径距离为:39.867984
经过22代,最优路径距离为:39.867984
经过23代,最优路径距离为:39.867984
经过24代,最优路径距离为:39.867984
经过25代,最优路径距离为:39.867984
经过26代,最优路径距离为:39.867984
经过27代,最优路径距离为:39.867984
经过28代,最优路径距离为:39.867984
经过29代,最优路径距离为:39.867984
经过30代,最优路径距离为:39.867984
经过31代,最优路径距离为:39.867984
经过32代,最优路径距离为:39.867984
经过33代,最优路径距离为:39.867984
经过34代,最优路径距离为:39.867984
经过35代,最优路径距离为:39.867984
经过36代,最优路径距离为:39.867984
经过37代,最优路径距离为:39.867984
经过38代,最优路径距离为:39.867984
经过39代,最优路径距离为:39.867984
经过40代,最优路径距离为:39.867984
经过41代,最优路径距离为:39.867984
经过42代,最优路径距离为:39.867984
经过43代,最优路径距离为:38.056051
经过44代,最优路径距离为:38.056051
经过45代,最优路径距离为:38.056051
经过46代,最优路径距离为:38.056051
经过47代,最优路径距离为:38.056051
经过48代,最优路径距离为:38.056051
经过49代,最优路径距离为:38.056051
经过50代,最优路径距离为:38.056051
经过51代,最优路径距离为:38.056051
经过52代,最优路径距离为:38.056051
经过53代,最优路径距离为:38.056051
经过54代,最优路径距离为:36.309216
经过55代,最优路径距离为:36.309216
经过56代,最优路径距离为:33.889863
经过57代,最优路径距离为:33.889863
经过58代,最优路径距离为:33.889863
经过59代,最优路径距离为:33.889863
经过60代,最优路径距离为:33.422234
经过61代,最优路径距离为:32.339747
经过62代,最优路径距离为:32.339747
经过63代,最优路径距离为:32.339747
经过64代,最优路径距离为:31.677589
经过65代,最优路径距离为:31.677589
经过66代,最优路径距离为:29.670782
经过67代,最优路径距离为:29.670782
经过68代,最优路径距离为:29.670782
经过69代,最优路径距离为:29.670782
经过70代,最优路径距离为:29.670782
经过71代,最优路径距离为:29.670782
经过72代,最优路径距离为:29.670782
经过73代,最优路径距离为:29.670782
经过74代,最优路径距离为:29.670782
经过75代,最优路径距离为:29.670782
经过76代,最优路径距离为:29.670782
经过77代,最优路径距离为:29.670782
经过78代,最优路径距离为:29.670782
经过79代,最优路径距离为:29.340520
经过80代,最优路径距离为:29.340520
经过81代,最优路径距离为:29.340520
经过82代,最优路径距离为:29.340520
经过83代,最优路径距离为:29.340520
经过84代,最优路径距离为:29.340520
经过85代,最优路径距离为:29.340520
经过86代,最优路径距离为:29.340520
经过87代,最优路径距离为:29.340520
经过88代,最优路径距离为:29.340520
经过89代,最优路径距离为:29.340520
经过90代,最优路径距离为:29.340520
经过91代,最优路径距离为:29.340520
经过92代,最优路径距离为:29.340520
经过93代,最优路径距离为:29.340520
经过94代,最优路径距离为:29.340520
经过95代,最优路径距离为:29.340520
经过96代,最优路径距离为:29.340520
经过97代,最优路径距离为:29.340520
经过98代,最优路径距离为:29.340520
经过99代,最优路径距离为:29.340520
经过100代,最优路径距离为:29.340520
经过101代,最优路径距离为:29.340520
经过102代,最优路径距离为:29.340520
经过103代,最优路径距离为:29.340520
经过104代,最优路径距离为:29.340520
经过105代,最优路径距离为:29.340520
经过106代,最优路径距离为:29.340520
经过107代,最优路径距离为:29.340520
经过108代,最优路径距离为:29.340520
经过109代,最优路径距离为:29.340520
经过110代,最优路径距离为:29.340520
经过111代,最优路径距离为:29.340520
经过112代,最优路径距离为:29.340520
经过113代,最优路径距离为:29.340520
经过114代,最优路径距离为:29.340520
经过115代,最优路径距离为:29.340520
经过116代,最优路径距离为:29.340520
经过117代,最优路径距离为:29.340520
经过118代,最优路径距离为:29.340520
经过119代,最优路径距离为:29.340520
经过120代,最优路径距离为:29.340520
经过121代,最优路径距离为:29.340520
经过122代,最优路径距离为:29.340520
经过123代,最优路径距离为:29.340520
经过124代,最优路径距离为:29.340520
经过125代,最优路径距离为:29.340520
经过126代,最优路径距离为:29.340520
经过127代,最优路径距离为:29.340520
经过128代,最优路径距离为:29.340520
经过129代,最优路径距离为:29.340520
经过130代,最优路径距离为:29.340520
经过131代,最优路径距离为:29.340520
经过132代,最优路径距离为:29.340520
最优解:
2—>8—>1—>10—>9—>11—>13—>7—>12—>6—>5—>4—>3—>14—>2
总距离:29.6708
-------------------------------------------------------------
历时 0.847846 秒。
二、灰色预测matlab算法模板
clear
syms a u;% 定义多个符号是符号变量
c=[a,u]';% 构成矩阵
A=sort(rand(1,20)) * 10;% 输入数据,可以修改
Ago=cumsum(A);% 原始数据一次累加,得到1-AGO序列xi(1)。
n=length(A);% 原始数据个数
for k=1:(n-1)
Z(k)=(Ago(k)+Ago(k+1))/2; % Z(i)为xi(1)的紧邻均值生成序列
end
Yn =A;% Yn为常数项向量
Yn(1)=[]; % 从第二个数开始,即x(2),x(3)...
Yn=Yn';
E=[-Z;ones(1,n-1)]';% 累加生成数据做均值
c=(E'*E)\(E'*Yn); % 利用公式来求出a,u
% c= c';
a=c(1);% 得到a的值
u=c(2);% 得到u的值
F=[];
F(1)=A(1);
for k=2:(n)
F(k)=(A(1)-u/a)/exp(a*(k-1))+u/a;% 求出GM(1,1)模型公式
end
G=[];% 空矩阵
G(1)=A(1);
for k=2:(n)
G(k)=F(k)-F(k-1);% 两者做差还原原序列,得到预测数据
end
t1=1:n;
t2=1:n;
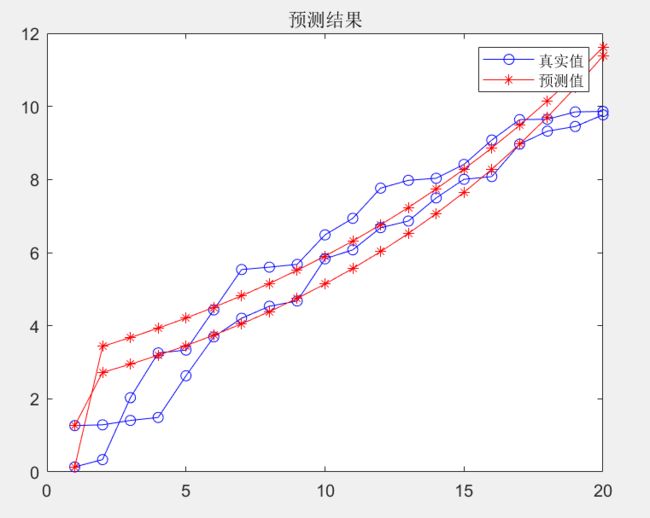
plot(t1,A,'bo-');
hold on;
plot(t2,G,'r*-');
title('预测结果');
legend('真实值','预测值');
% 后验差检验
e=A-G;
q=e/A;% 相对误差
s1=var(A);
s2=var(e);
c=s2/s1;% 方差比
len=length(e);
p=0; % 小误差概率
for i=1:len
if(abs(e(i))<0.6745*s1)
p=p+1;
end
end
p=p/len;
输出:
相对误差q = -0.0061
方差比c = 0.1096
小误差概率p = 1