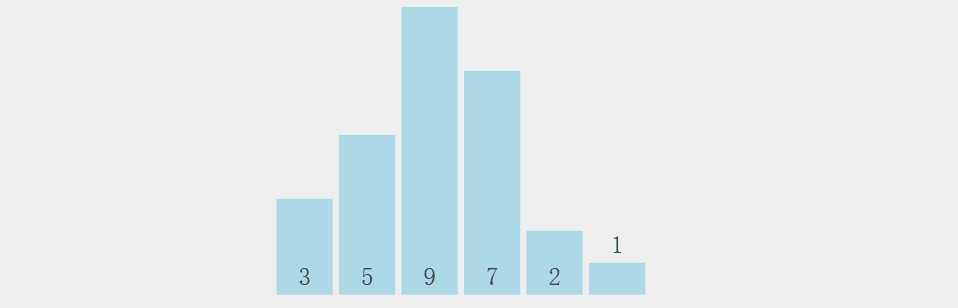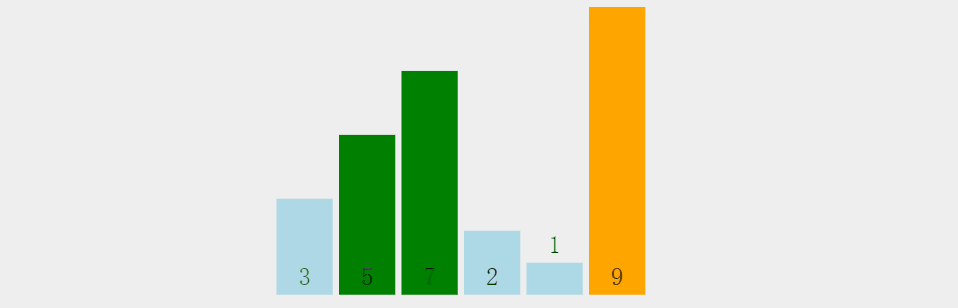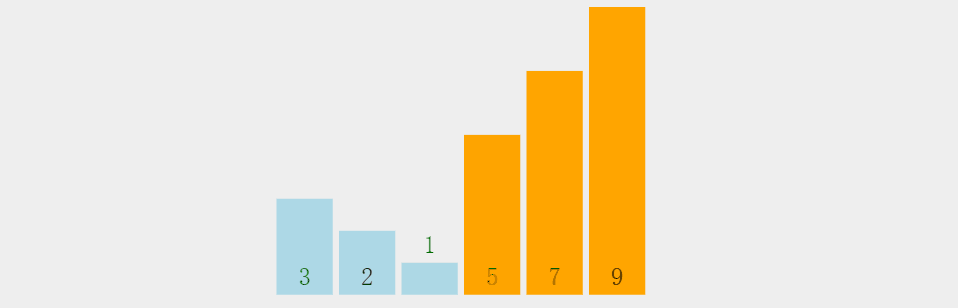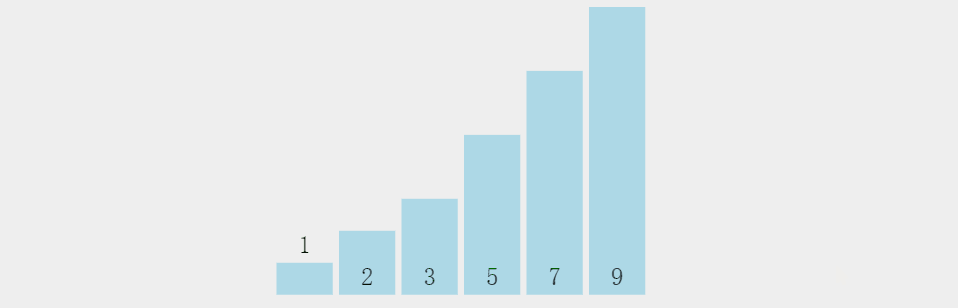万字梳理：算法0基础入门-主流排序算法大集合；硬核整理图解+代码--数据结构与算法小结4

本期脑图：

1.前言：谈算法色变？Duck不必！

    不知你是否有这种感受？一提到算法，第一反应就是：太难了，我不会！一开始我也有过这种感受，不过耐心学下去之后发现，算法并没有那么复杂。至少入门是一件很容易的事情，只需要：

    1.耐心看完本篇推文！

    2.开始思考任意一个算法实现思路！

    3.自己尝试写任意一个实现代码！

只要成功写出一个，你就入门了，你一定可以做到！至于后期深入到什么程度，就取决于你付出的时间多久了~

2.一定要掌握算法吗？

    个人认为：这取决于对自己的要求，如果对自我的要求是做一个普通的开发人员，不学算法问题不大。日常应付CRUD简单需求就可以了（一般月薪2W就是天花板了）。

    但是如果想成为一个高级开发工程师或者想入大厂，年薪50W以上，算法是必过的一个门槛，大厂的面试中光是算法板块就可以卡掉很多人~所以算法重要与否，主要取决于对自己的要求！

            下图为一位面试过某跳动大厂遇到的两个算法题的其中一个：

3.开始入门：排序算法

    算法有很多，本篇入门主讲排序算法；生活当中有很多场景需要用到排序，比如经常逛淘宝，有人就需要按照价格从低到高来排序；再比如我们经常看到的微博热搜排名，其实也是一种根据用户点击量进行的排序，可以说生活无处不排序，那么多排序，底层到底怎么做的呢？排序算法走起~

    排序算法按照不同标准可以分为不同类，不过就入门而言知道这些分类名称帮助不大，所以省掉那些复杂的，直接按照难易程度分成两类：

    一 简单排序：1.冒泡排序    2.选择排序    3.插入排序（适合入门）

    二 复杂排序：1.希尔排序    2.归并排序    3.快速排序（适合进阶）

    3.1    冒泡排序

        建议：算法学习三步走：（偶尔四步）

    第一步：什么是冒泡排序？

        冒泡排序（Bubble Sort）：重复地访问要排序的元素列，依次比较两个相邻的元素，如果顺序符合要求（如从大到小）就把他们交换过来。此过程重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同水中气泡最终会上浮到顶端一样，故名“冒泡排序”。上例子：

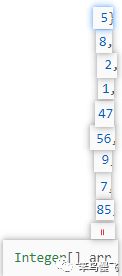
一个数组长这样：

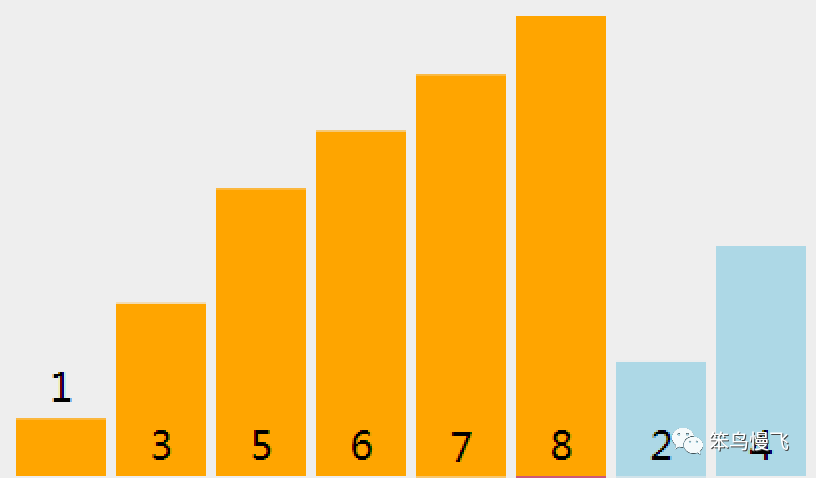
Integer[] arr = {85, 7, 9, 56, 47, 1, 2, 8, 5};

假如竖着看，就变成这样：

所以现在要做的就是将数组中的 数值大的元素“浮”到上面，就像吐泡泡，上面的泡泡更大（数值更大）；（配图仅仅为了更便于理解）

    第二步：冒泡排序算法图解

    需求，一串数组：3 5 9 7 2 1，要求排序后结果从小到大：1 2 3 5 7 9。

先看一下冒泡排序整体过程，有个整体印象：

    第一轮冒泡分解步骤（每一轮过程相似）：

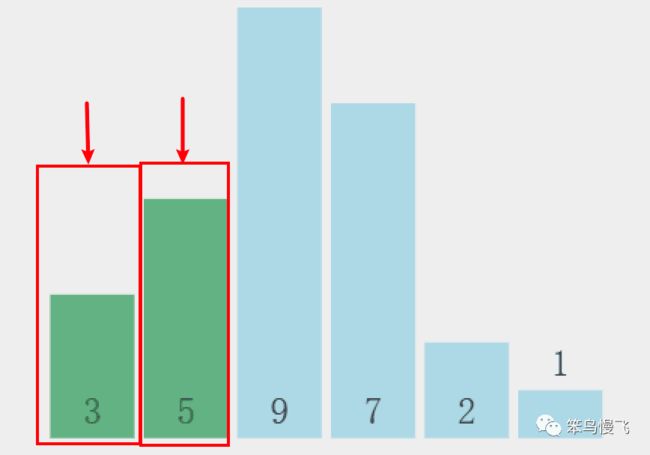
1.元素3和相邻元素5比较，3<5，不交换位置；

2.元素5和元素9比较大小：5<9，不交换位置；

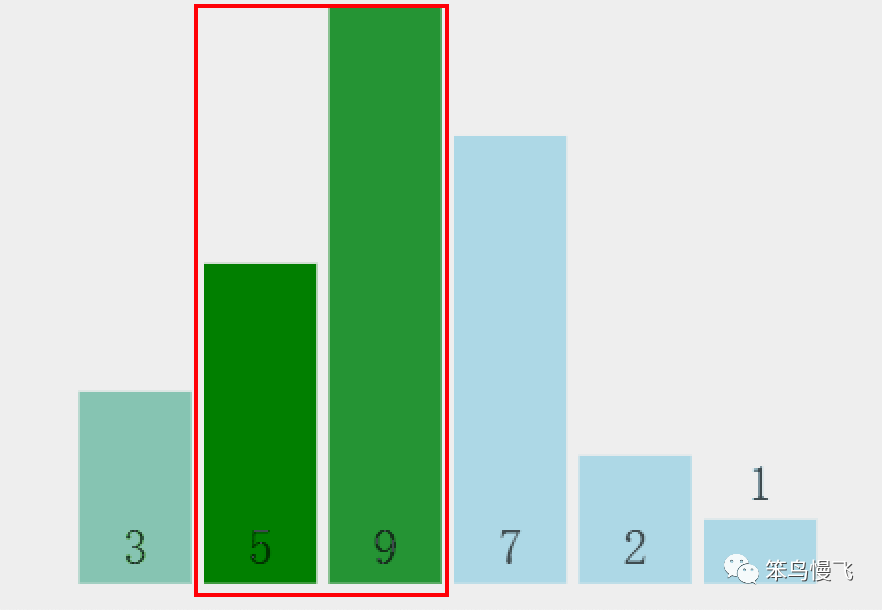
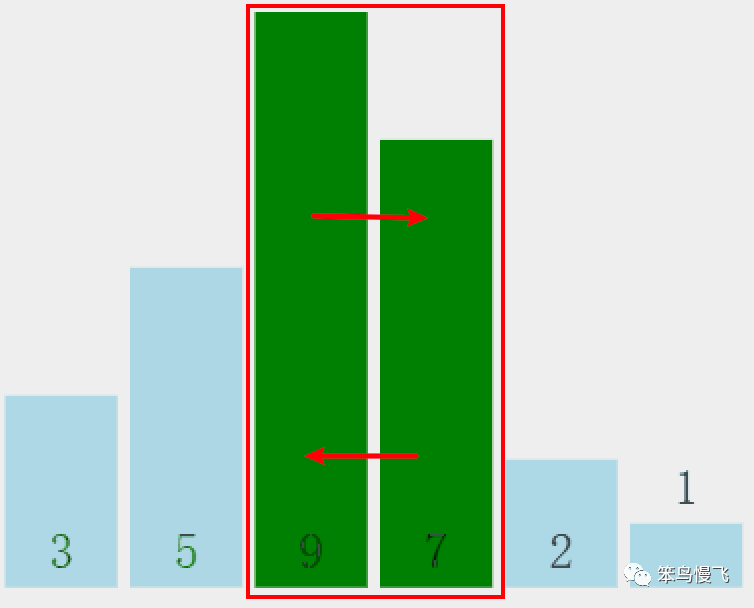
3.元素9和元素7比较大小：9>7，交换位置；

4.换到新位置的元素9和元素2比较大小：9>2，交换位置；

5.换到新位置的元素9和元素1比较大小：9>1，交换位置，右边没有元素，第一轮结束；

6.第一轮冒泡结束后数组现状：最大元素找到相应位置；

第二轮冒泡排序：将第二大的元素放在对应位置；

第三轮冒泡排序：将第三大的元素放在对应位置；

第四轮冒泡排序：将第四大的元素放在对应位置；

第五轮冒泡排序：将第五大的元素放在对应位置；

也就是说有N个元素，就会有N-1轮排序；每一轮交换过程类似，在此不做赘述；

    第三步 手写代码实现冒泡排序

    需要实现的API：（建议先自己先code一下，过程比结果更重要）

1.sort(Comparable[] a)：遍历， 调用greater和exchange方法完成排序；

2.greater(Comparable c1, Comparable c2)：比较两个相邻元素的大小；

3.exchange(Comparable[] a, int b, int c) ：交换两个元素的位置；

后续排序算法实现均需要greater（）；exchange（）；后续将不再列出；

public class MyBubble {    //排序    public static void sort(Comparable[] a) {        //有length-1个元素需要进行交换的过程        for (int i = 0; i < a.length - 1; i++) {            //要从索引0处的元素开始交换，最坏情况一直交换到length-1次；            for (int j = 0; j < a.length - 1 - i; j++) {                //比较假如a[j]比a[j+1]大，则交换位置                if (greater(a[j], a[j + 1])) {                    exchange(a, j, j + 1);                }            }        }    }    //比较大小    public static boolean greater(Comparable c1, Comparable c2) {    /*    //return c1.compareTo(c2) > 0; 的拆解版：    int compare = c1.compareTo(c2);    return compare > 0;*/        return c1.compareTo(c2) > 0;    }    //交换位置    public static void exchange(Comparable[] a, int b, int c) {        //建立一个临时元素，用于交换中转        //第一个函数等号后面的元素就是下一个函数的等号前面的元素，首尾衔接，即完成交换        Comparable num = a[b];        a[b] = a[c];        a[c] = num;    }}

        补充：精力充沛的可以思考一下冒泡排序的时间复杂度是多少？

提示，假设冒泡排序的最坏情况：一个含有N个元素的完全倒序的数组需要交换多少次完成排序？

        推导过程（过程比结果更重要！）

    第一个元素需要交换的次数：N-1

    第二个元素需要交换的次数：N-2

    第三个元素需要交换的次数：N-3

    ......

    第N-1个元素需要交换的次数：1

    第N个元素不需要交换，此时已经正序了；

    最后一共需要交换次数：1+2+3+...+N-1 = (N*(N-1))/2=N^2/2 - N/2;

    按照时间复杂度的去杂规则，最后时间复杂度简化为：

    F（N）= O(N^2)；

    3.2    选择排序

    第一步    什么是选择排序？

    选择排序（Selection sort）的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。（看不懂就跳到步骤详解）

    第二步：选择排序算法图解

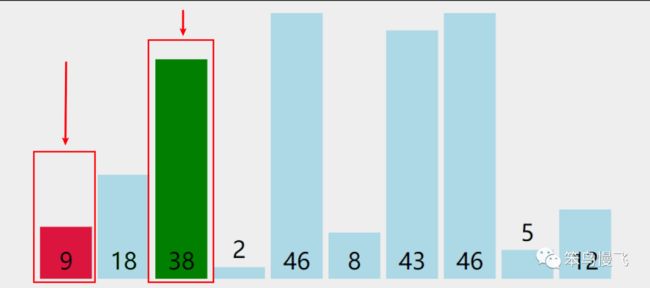
    需求，一串数组：9 18 38 2 46 8 43 46 5 12，要求结果从小到大顺序排序

先看一下选择排序整体过程，有个整体印象：

绿色为遍历过程；

红色为当前最小元素索引位置标记；

橙色为已经排好序的元素，且不参与下一轮排序；

    

    第一轮排序分解步骤（每一轮过程相似）：

    1.元素9和相邻元素18比较，9<18，红色标记记录9索引位置0；

    2.元素9和元素38比较，9<38，红色标记记录9索引位置0；

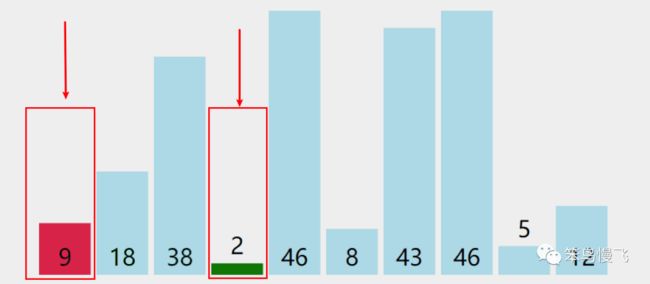
    3.元素9和元素2比较，2<9，红色标记记录2索引位置3；

    4.元素2和元素46比较，2<46，红色标记记录2索引位置3；

    5.元素2和元素8比较，2<8，红色标记记录2索引位置3；

（后续比较过程一致，so省掉部分图）

    6.元素2和元素43比较，2<43，红色标记记录2索引位置3；

    7.元素2和元素46比较，2<46，红色标记记录2索引位置3；

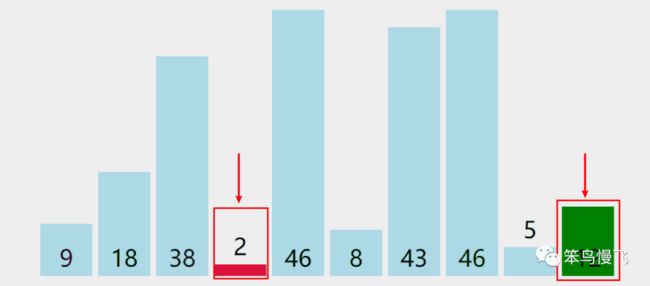
    8.元素2和元素5比较，2<5，红色标记记录2索引位置3；

    9.元素2和元素12比较，2<12，红色标记记录2索引位置3；

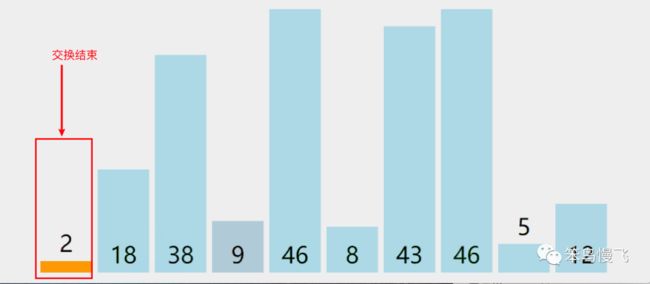
    10.红色标记最终记录最小元素索引为3，交换索引0和索引3的元素，第一轮结束；

第二轮排序：将第二小的元素放在1索引位置；

第三轮排序：将第三小的元素放在2索引位置；

第四轮排序：将第四小的元素放在3索引位置；

第五轮排序：将第五小的元素放在4索引位置；

。。。。。。

也就是说有N个元素，就会有N-1轮排序；每一轮交换过程类似，在此不做赘述；

    第三步 手写代码实现选择排序

（有前面冒泡排序基础，这个不难实现，尝试自己code代码吧）

    需要实现的API：

1. sort(Comparable[] a)：遍历， 调用greater和exchange方法完成排序；

   下面两个API前面实现过，用现成的即可（且后续算法实现不再展示）

    2.greater(Comparable c1, Comparable c2)；

    3.exchange(Comparable[] a, int b, int c) ；

/** * 2.选择排序 * 思路：每一轮先假定第一个元素是最小的，依次用第一个元素比较后面每一个 * 比较之后，确定最小值并后续更新最小值 * ！最后！再互换元素 * 代码思路(双循环)： */public static void selectSort(Comparable[] arr) {    //1.外循环条件：互换位置操作一共需要arr.length - 1次    for (int i = 0; i < arr.length - 1; i++) {        //2.indexMin用于储存每轮最小元素索引        int indexMin = i;        //3.第i轮中内循环条件：用indexMin处的元素依次和后面每一个比较，确定最小元素索引        for (int j = i + 1; j < arr.length; j++) {            if (greater(arr[indexMin], arr[j])) {                //记录最小元素下标                indexMin = j;            }        }        //互换元素        exchange(arr, i, indexMin);    }}

    补充：请问选择排序的时间复杂度是多少呢？

    选择排序的时间复杂度分析：选择排序使用了双层for循环，其中外层循环完成了数据交换，内层循环完成数据比较：

数据比较次数：(N-1)+(N-2)+(N-3)+...+3+2+1 = N^2/2 - N/2

数据交换次数:N-1 次

时间复杂度F（N）= N^2/2 - N/2 +N-1 =N^2/2 + N/2 - 1=O(N^2)

3.3    插入排序

    第一步    什么是插入排序？

    插入排序的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增1的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动，举一个形象的例子就是玩扑克牌，玩家拿到一副乱的牌，开始整理，方式为：每次拿出剩下所有牌里最小的一个牌，放在最前面的位置；

再拿出稍大的牌放在第二的位置，以此类推，这就是一个插入排序；（看不懂就跳到步骤详解）

    第二步：插入排序算法图解

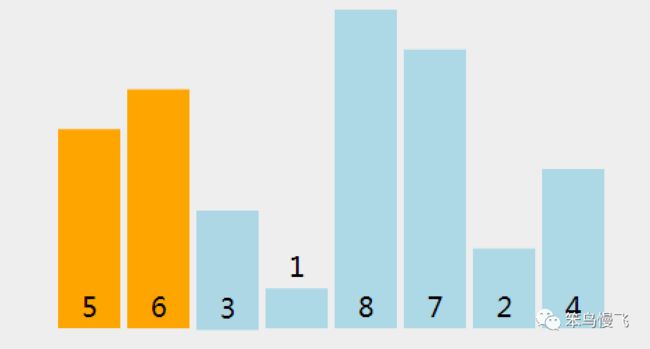
    需求，一串数组：5 6 3 1 8 7 2 4，要求结果从小到大顺序排序

老规矩，看图：

绿色为被向后位移的元素；

红色为正在操作的需要插入的元素；

橙色为暂时排好序的元素；

    第一轮排序分解步骤（从索引1处开始）：

    1.索引1处的元素6和索引0的5元素比较，5<6，按兵不动；

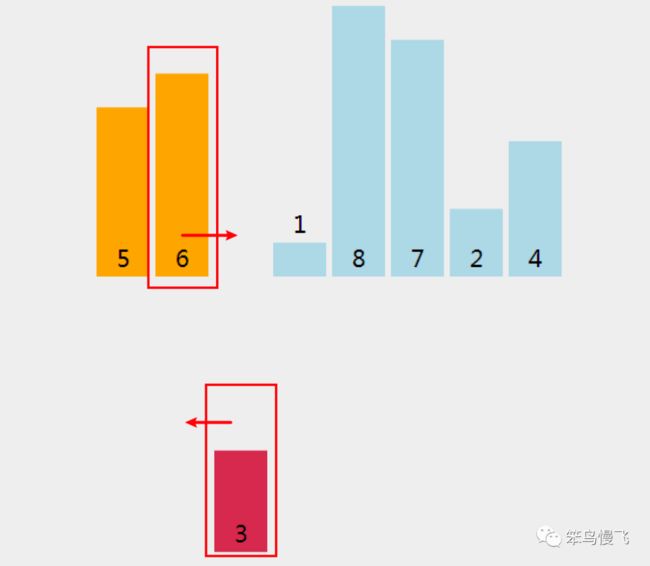
    2.索引2处的元素3和前面的元素6比较，3<6，换位置；

元素3和索引0的元素5比较，3<5，换位置

没有元素可以比较了，插入；

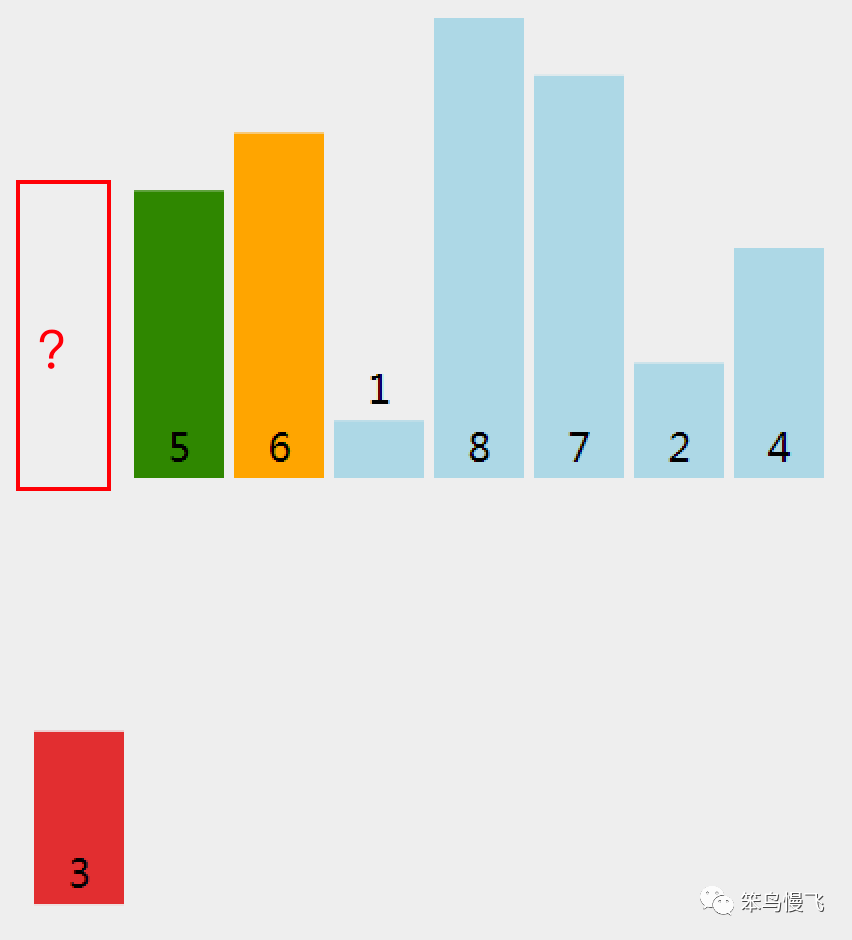
3.索引3处的元素1和前面的元素6比较，1<6，换位置；

    3.1    元素1和更前面的元素5比较，1<5，换位置；

    3.2    元素1和更前面的元素3比较，1<3，换位置；

    3.3    元素1没有元素可以比较，插入位置；

完成上述过程后：

4.索引4处的元素8和前面的元素6比较，6<8，找到比自己小的元素了，按兵不动；

5.索引5处的元素7和前面的元素8比较，7<8，换位置；

    5.1    元素7和更前面的元素6比较，6<7，找到比自己小的元素了，按兵不动；

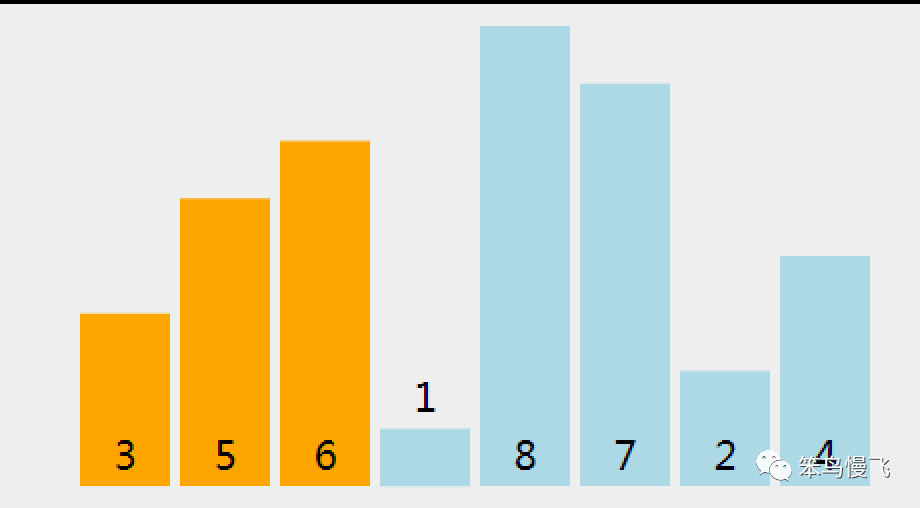
完成上述过程后：

6.索引6处的元素2和前面的元素们比较，后续操作相同；

7.索引7处的元素4和前面的元素们比较，后续操作相同；

最终如下：

第三步 手写代码实现插入排序

（尝试自己code代码吧！！！）

    需要实现的API：

1. sort(Comparable[] a)：遍历， 调用greater和exchange方法完成排序；+greater(...)+exchange(...) ;

/** * 3.插入排序 * 思路：从数组中的第二个位置的元素开始插入 * 依次和前面元素进行比较，同样操作执行到数组的最后一个位置 * 代码思路(双循环)： */public static void insertingSort(Comparable[] arr) {    //1.外循环条件：互换位置操作一共需要arr.length - 1次    //条件可以写成i < arr.length；也可写成i <= arr.length - 1    for (int i = 1; i < arr.length; i++) {        for (int j = i; j > 0; j--) {            if (greater(arr[j - 1], arr[j])) {                exchange(arr, j - 1, j);            }        }    }}

​​​​​​​

补充：请问插入排序的时间复杂度是多少呢？    tips：考虑最坏的情况进行计算，即  <8 7 6 5 4 3 2 1>;    推理方式和上个类似：    时间复杂度F（N）= O(N^2)；

（恭喜你！坚持看到这里，并且将代码实现出来的话，你已经一只脚成功迈进算法的大门啦！）

    有没有发现，简单排序的时间复杂度都是O(N^2)，随着数据量的增加，所消耗的时间量也是非常大的，那有没有时间复杂度低一些的排序算法：时间复杂度低，但是同样可以达到效果的呢？

    有的，就是接下来的复杂排序！

    在上面的插入排序中，假如需要排序的数列刚好是逆序的，如

数列1：{9,8,7,6,5,4,3,2,1}

和

数列2：{2,4,6,8,1,3,5,7,9}

那插入排序需要的操作次数对比结果是显而易见的：数列1>数列2

那排序优化方向就是：使需要操作的数列本身就是比较有序的，就可以减少操作次数，降低时间复杂度。那应该怎么做呢？希尔排序就是对数列进行“优化”操作的方式之一；

    3.4    希尔排序

    第一步    什么是希尔排序？（建议直接看分步骤图解）

   希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。

    希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。（来自度娘，看不懂 强烈建议看图解，理解过程几乎等同于理解了定义）

    第二步：希尔排序算法图解

    希尔排序的核心就是定义一个梯度gap，根据h将数列分成不同组，在不同组内先进行插入排序，然后最后再以gap=1，也就是整个数列进行插入排序；因为前面的操作已经将数列变得相对更加有序，所以最后一次插入排序需要的交换次数大大减少；

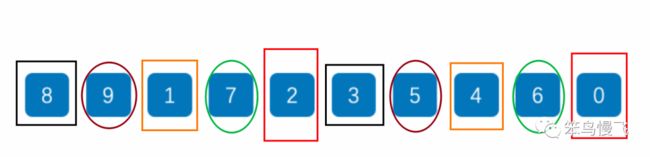
    需求，一串数组：8 9 1 7 2 3 5 4 6 0，要求结果从小到大顺序排序；

动图：

第一轮希尔排序分解步骤：

1.第一轮分组插入排序，首先确定梯度gap为10/2=5，那么分组情况如下：

1组	索引0处的8	索引0+5处的3
2组	索引1处的9	索引1+5处的5
3组	索引2处的1	索引2+5处的4
4组	索引3处的7	索引3+5处的6
5组	索引4处的2	索引4+5处的0

2.将同一个组依次进行分组插入排序；

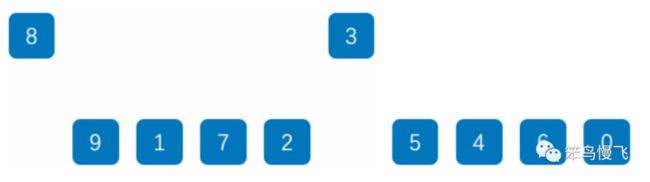
    2.1 先将索引0处的8和索引0+5处的3进行插入排序操作；

    排序后：

    2.2 将索引1处的9 和索引1+5处的5进行插入排序操作；

    2.3 将索引2处的1 和索引2+5处的4进行插入排序操作；

    。。。后续操作相同，直到完成最后一个小分组的排序操作；

第一轮结束后，数列变得更加相对有序了：

第二轮分组插入排序：

    1.确定梯度gap为gap/2=2（余数去掉），那么新的分组情况如下：

第一组	索引0，2，4，6，8处的{3,1,0,9,7}
第二组	索引1，3，5，7，9处的{5,6,8,4,2}

    2.依次对两个小分组组内进行插入排序后；

    （因为插入排序之前已经分步骤图解很清楚啦，这里就不浪费笔墨啦）

第三轮分组排序：

    1.确定梯度gap为gap/2=1（余数去掉），那么新的分组就是整个数列啦，剩下就和插入排序一毛一样啦，所以直接po最后结果

来个小总结：理解希尔排序的重点就是对于每一次的分组梯度的理解；

 第三步 手写代码实现希尔排序

PS ：难度升级了，我把这块琢磨通花了好久，最终发现有两个理解上的关键点：

1.梯度h（代码我用的h字符代表梯度）的理解    

2.在代码实现找到待插入元素时候，可以从前向后（就像实现插入排序一样从索引1处依次遍历），也可以从后往前（从最后一处索引依次向前）；

对于我而言，发现从后向前实现会更容易理解！

代码如下：

//希尔排序思路，每轮按照不同梯度将数组分组，将每个小分组使用插入排序；public static void shellSort(Comparable[] arr) {    //初始化梯度h    int h = 1;    while (h < arr.length / 2) {        h = 2 * h + 1;    }    //按照梯度进行分组    while (h >= 1) {        //1.找到待插入的元素        for (int i = h; i < arr.length; i++) {            //第二个for循环一定要理解好；            //int j = i：含义为找到每次需要移动并插入到有序数组的元素            //j >= h：含义为 临界值为>=h，这样保证下面j-h不会超出            //j -= h：小组内插入排序是先从后往前依次进行            //2.把待插入的元素插入到有序数列中            for (int j = i; j >= h; j -= h) {                //待插入的元素是arr[j]，比较arr[j]和arr[j - h]                if (greater(arr[j - h], arr[j])) {                    exchange(arr, j - h, j);                } else {                    //待插入元素已经找到合适位置，结束循环                    break;                }            }        }        //梯度减半        h /= 2;    }}

    希尔排序时间复杂度有点特殊，它略微优于O(n^2),但是性能由不及O(nlogn),在此做了解即可，重点是要至少得掌握冒泡排序和归并排序的时间复杂度的推导过程；

3.5    归并排序

    第一步    什么是归并排序；

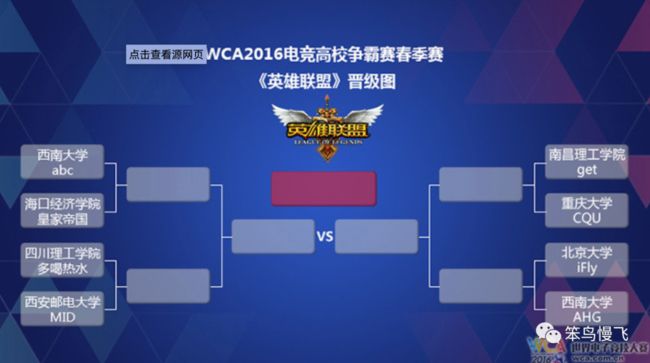
    首先，先给大家po个图，一定非常感兴趣！是的就是职业电竞比赛的晋级图，比方说，很多团队要争锋冠军，怎么评比呢？就是采用分散晋级的方式，首先选出八强，然后是四强，两强决赛最后决出冠军；

    假如现在的需求不是选出最强，而是按照战斗力从左到右排成一排呢？那就变成了现在要讲到的归并排序！！！这种先分开比较再合并的过程叫归并（merge）；

    第二步：归并排序算法图

需求：一串数组：{3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};

要求结果从小到大顺序排序；

欸~这次先看一下分解图，再看动图（因为之前我发现自己看不懂动画，分解之后才看明白，所以学习方式得灵活多样不能同一个方式走到黑啊！）

    为了方便，我就取了八个元素进行演示，分解图如下：

分开：

合并：（红色箭头指向的都是有排序交换操作的，仔细看和上图区别）

接下来看动图应该就可以看懂了：

PS：相同颜色为同一个小分组；

第三步 手写代码实现归并排序（首先需要理解递归的概念和使用）：

    需要实现的API：

成员方法：​​​​​​​

1.public static void mergeSort(Comparable[]arr):对数组arr内的元素进行排序；2.private static void mergeSort(Comparable[]arr,int low,int high):对数组arr中的索引low到索引high之间的元素进行排序；3.private static void merge(Comparable[]arr,int low,int middle,int high):从索引low到索引middle为一个子组，从索引mid+1到索引high为另一个子组，把数组中arr的这两个子组中的数据合并成一个有序的大组（从索引low到索引high）；4.private static boolean greater(Comparable a,Comparable b);判断a是否大于b；5.private static boolean exchange(Comparable[] arr,int a,int b);交换arr中，索引a和索引b处的值；成员变量：6.private static Comparable[] temp：此为临时数组；

代码code：​​​​​​​

/** * 5.归并排序 * 对数组arr内的元素进行排序； *///定义临时数组进行元素的储存（可以理解为用空间换时间）private static Comparable[] temp;public static void mergeSort(Comparable[] arr) {    //初始化临时数组，长度为arr.length    temp = new Comparable[arr.length];    //定义索引源头和结尾处    int low = 0;    int high = arr.length - 1;    //调用重载    mergeSort(arr, low, high);}/** * 对数组arr中的索引low到索引high之间的元素进行排序； * * @param arr 需要拆分的数组 * @param low 需要拆分的索引头 * @param high 需要拆分的索引尾 */private static void mergeSort(Comparable[] arr, int low, int high) {    //做安全校验    if (high <= low) {        return;    }    //从low到high分组（比如5-9，就分成5-6;7-8-9）    int middle = low + (high - low) / 2;    //递归,分组    mergeSort(arr, low, middle);    mergeSort(arr, middle + 1, high);    //合并    merge(arr, low, middle, high);}/** * 从索引low到索引middle为一个子组，从索引mid+1到索引high为另一个子组 * 把数组中arr的这两个子组中的数据合并成一个有序的大组（从索引low到索引high） * * @param arr 需要拆分的数组 * @param low 需要拆分的索引头 * @param middle 中间位置的索引 * @param high 需要拆分的索引尾 */private static void merge(Comparable[] arr, int low, int middle, int high) {    //定义3个指针i,p1,p2    int i = low;    int p1 = low;    int p2 = middle + 1;    //比较两个指针指向的索引的元素大小，将小的放入temp临时数组中    while (p1 <= middle && p2 <= high) {        if (greater(arr[p1], arr[p2])) {            //p1>p2,放p2            temp[i++] = arr[p2++];        } else {            //放p1            temp[i++] = arr[p1++];        }    }    //如果其中一个指针已经走完，循环另外一个小数组放入temp数组中；    while (p1 <= middle) {        temp[i++] = arr[p1++];    }    while (p2 <= high) {        temp[i++] = arr[p2++];    }    //把temp数组放回原数组    for (int j = low; j <= high; j++) {        arr[j] = temp[j];    }}

    归并排序时间复杂度分析

（精力允许可以看，看到这里有些吃力可以跳过，暂时不理解没关系的）：

    举一个最悲观的一种情况也就是完全逆序，来算时间复杂度：

    如果一个数组{8,7,6,5,4,3,2,1}；一共有8个元素，所以要拆分:log2(8)次=3次，也就是一共有3层；

    如第f=2层有 2^f=4个子数组，需要比较2次归并；

    也就是说第f层的元素有 2^f个子数组；

    每个子数组的长度为2^(3-f)；

    最多需要比较2^(3-f)次后归并；

    每一层一共最多需要：子数组个数*每个子组需要次数= 2^f*2^(3-f)=2^3 = 8;

    那么3层一共为3*2^3= 24;

推导演算过程：（需要自己手写推导）

    假设元素个数为N，需要拆分log2(N)次，一共有log2(N)层；

    所有层需要交换的次数为：

    =log2(N)*2^(log2(N)) = log2(N)*N

    这里有点绕，得静下心好好推导一下才行，但是一旦想明白，就不会忘记了；

    根据大O推导法则，最终归并排序时间复杂度为：O(NlogN);

3.6    快速排序

    第一步    什么是快速排序？

    快速排序算法通过多次比较和交换来实现排序，其排序流程如下： 

(1)首先随机选择一个元素作为分界值，通过该分界值将数组分成左右两部分。

(2)将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。

(3)然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

(4)重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了

这次看懂官方定义了，继续看图解，No picture ，Say 个J8；

    第二步    快速排序算法图解

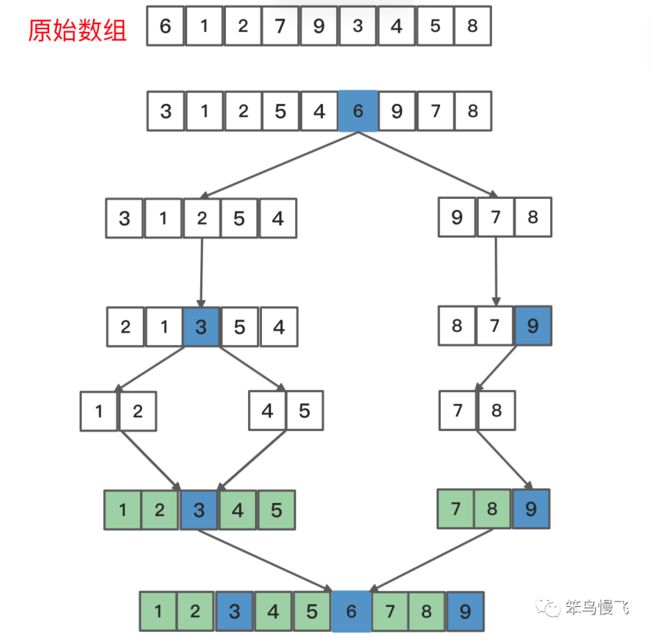
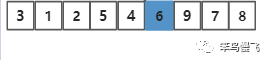
    需求：一串数组：{6,1,2,7,9,3,4,5,8}，要求结果从小到大顺序排序；

一般是选择第一个元素作为基准元素，这里就是位于索引0的6；

并且使得比6大的元素移动到数列右边，比它小的元素移动到数列的左边，从而把数列拆分成两个部分，后续以此类推，会将拆分后的两个部分再次选择第一个元素作为基准元素，重复上述步骤，直到不可再分；

加上备注：

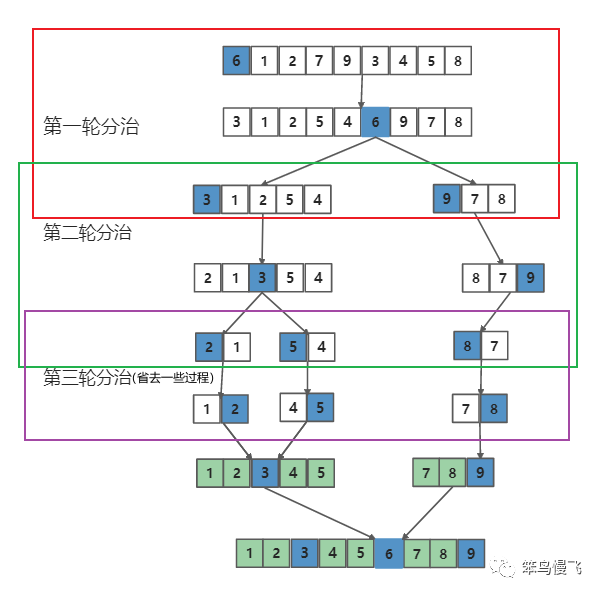
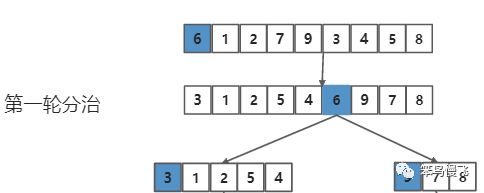
第一轮分治（红色框框）放大详解：（选择索引0处的6作为基准元素）：

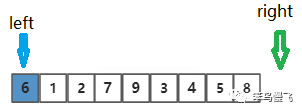
原始数组长下面这样：

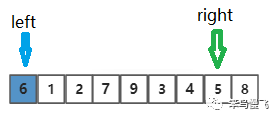
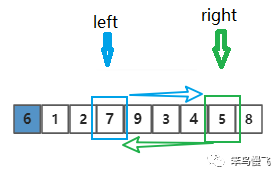
第一步，首先right指针先向左移动一位

（--right），然后和基准元素进行比较，6<8;

第二步，因为6<8，所以right指针继续向左移动一位（--right），然后和基准元素进行比较，6>5,Yeah！找到比基准元素小的元素啦~;

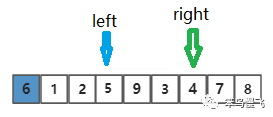
第三步，因为right指针找到比基准元素小的元素了，切换到left指针向右移动一位（++left），然后和基准元素进行比较，6>1;

第四步，因为left指针没找到比6大的元素，left继续向右移动一位（++left），然后和基准元素进行比较，6>2;

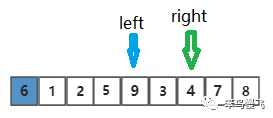
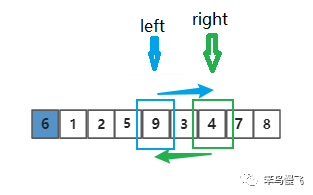
第五步，同理，left继续向右移动一位（++left），然后和基准元素进行比较，6<7;Yeah！找到比基准元素大的元素啦~;

第六步，因为left指针和right指针都找到目标元素啦，开始交换两者位置；

第七步，交换结束后，切换到right指针，且向左移动一位，和基准元素比较，6<4,找到比基准小的元素啦；

第八步，切换到left指针且向右移动一位，比较：9>6,找到比基准元素大的元素啦；

第九步，交换left和right指针的元素；

第十步，切换到right指针并向左移动一位，比较：6>3,找到比基准元素小的元素啦；

第十一步，切换到left指针并向右移动一位，发现left和right重合，触发机制：和基准元素交换；

交换之后结果长这样~ ，~

第十二步，以基准元素6为中心，左右切分两个小分组，进行下一轮拆分排序，且原基准元素不参与下一轮分治；第一轮分治结束，后续类似；

注：这个算法的代码实现有多个方式；

    第三步 手写代码实现快速排序

需要实现的API：

成员方法：​​​​​​​

1.public static void sort(Comparable[]arr):对数组arr内的元素进行排序；2.private static void sort(Comparable[]arr,int low,int high):对数组arr中的索引low到索引high之间的元素进行排序；3.private static int partition(Comparable[]arr,int low,int middle,int high):从索引low到索引middle为一个子组，从索引mid+1到索引high为另一个子组，把数组中arr的这两个子组中的数据合并成一个有序的大组（从索引low到索引high）；4.private static boolean greater(Comparable a,Comparable b)
5.private static boolean exchange(Comparable[] arr,int a,int b);交换arr中，索引a和索引b处的值；

代码code：​​​​​​​

/** * 6.快速排序 * @param arr */public static void quickSort(Comparable[] arr) {    //初始化临时数组，长度为arr.length    temp = new Comparable[arr.length];    //定义索引源头和结尾处    int low = 0;    int high = arr.length - 1;    //调用重载    quickSort(arr, low, high);}private static void quickSort(Comparable[] arr, int low, int high) {    //做安全校验    if (high <= low) {        return;    }    //需要对数组中从low到high处的元素进行分组，左子组和右子组；    int partition = partition(arr, low, high);    //让左子组有序(partition - 1是因为临界值不参与排序)    quickSort(arr, low, partition - 1);    //让右子组有序    quickSort(arr, partition + 1, high);}/** * 需要对传进来的arr进行分两个组 * * @param arr  需要分组的arr * @param low  分组起始索引 * @param high 分组终止索引 * @return 返回新的临界点 */private static int partition(Comparable[] arr, int low, int high) {    //临界分界值    Comparable key = arr[low];    //定义两个指针，分别指向最小索引和最大索引的下一个位置    int left = low;    int right = high + 1;    //扫描切分    while (true) {        //首先从右往左扫描，找到比基准小的元素停止        while (greater(arr[--right], key)) {            //安全校验            if (right == low) {                break;            }        }        //首先从左往右扫描，找到比基准大的元素停止        while (greater(key, arr[++left])) {            //安全校验            if (left == high) {                break;            }        }        //当right<=left时候，停止循环，交换key和两指针停的位置        if (right <= left) {            exchange(arr, low, right);            break;        } else {            //交换            exchange(arr, left, right);        }    }    return right;}

    时间复杂度推导过程和归并排序类似  ：在每一轮的拆分分治后，原数组都会被拆分成两部分，然后在下一轮会继续被拆分成两部分，直到不能再拆分，每一轮的比较和交换，都需要把数组遍历一次，因此O(n),这种遍历平均情况下会需要log(n),所以~

    F(N)=O(NlogN);

4.总结

1. 学算法，思考过程比结果更重要，当然代码实现出来，才能变成自己的真功夫！

2. 倘若真的想好好学某一个技术，去看书吧，虽然我也是在写公众号的博主，但是我还是强烈安利去看书，如果实在看不下去就以专题为单位看视频，然后再看书，总之就是一定要看书！

3. 其实本篇很多的代码写法还有很多漏洞，就是有一些特殊情况没有考虑很全面，比如快速排序中：使用每个子数组的第一个位置的元素作为基准元素，在完全逆序情况之下的时间复杂度反而是更高的；除了使用递归之外，也可以使用栈的方式来实现这些排序算法，这样就可以从更底层去完成，等等等等，有很多需要优化的；不过作为入门而言，本篇足够了；