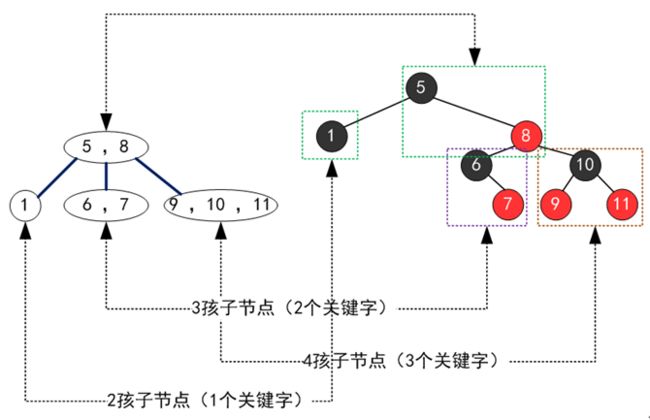
- Redis 源码分析-内部数据结构 robj
笨手笨脚の
#Redisredis数据结构数据库redisObject44字节embStrraw
Redis源码分析-内部数据结构robjRedis中,一个database内的这个映射关系是用一个dict来维护的(ht[0])。dict的key固定用一种数据结构来表达就够了,即动态字符串sds。而value则比较复杂,为了在同一个dict内能够存储不同类型的value,这就需要一个通用的数据结构,这个通用的数据结构就是robj(全名redisObject)。#defineLRU_BITS24/
- redis内部数据结构(5)-quicklist
Tinner丶
链表数据结构算法javaredis
Redis对外暴露的list数据类型,它底层实现所依赖的内部数据结构就是`quicklist`。我们在讨论中还会涉及到两个Redis配置(在redis.conf中的ADVANCEDCONFIG部分):12list-max-ziplist-size-2list-compress-depth0注:本文讨论的quicklist实现基于Redis源码的3.2分支。quicklist概述Redis对外暴露的
- Redis内部数据结构quicklist详解
码农单克
redisredis
在本文中,我们介绍一个Redis内部数据结构——quicklist。Redis对外暴露的list数据类型,它底层实现所依赖的内部数据结构就是quicklist。我们在讨论中还会涉及到两个Redis配置(在redis.conf中的ADVANCEDCONFIG部分):list-max-ziplist-size-2list-compress-depth0我们在讨论中会详细解释这两个配置的含义。注:本文讨
- redis操作zset类型的基本命令
JavaWeb学起来
redisredis数据结构
zset是有序存储的数据结构,它和set一样,不允许重复的值,下面我们总结一些常用的命令。zaddkey排序的数值值(这里为了zset可以有序的存储,需要设定数值)127.0.0.1:6379>zaddz15java3redis1mysql2nginx4oracle(integer)5zcardkey(返回key中的成员数)127.0.0.1:6379>zcardz1(integer)5zrang
- vue中el-tree的懒加载
zhz5214
vuevue.jselementuijavascript前端
el-tree是ElementUI中的一种树形控件,它可以在页面中显示树形数据结构,同时支持懒加载。懒加载是指在Vue组件渲染的过程中,只加载当前可见的部分数据,而不是一次性加载整个数据。这种方法可以显著提高页面的加载速度和响应性能,特别是在大型数据集上。要使用el-tree的懒加载功能,需要在树形控件组件中提供一个load方法。load方法会在展开一个父节点时触发,它的参数包含了父节点的数据和一
- 基础知识《Redis解析》
Hum8le
redis数据库缓存安全web安全
Redis详细解析与介绍Redis(RemoteDictionaryServer)是一个开源的高性能键值对(Key-Value)数据库,支持多种数据结构(如字符串、哈希、列表、集合等),广泛应用于缓存、消息队列、实时数据分析等场景。核心特点:内存存储:数据主要存储在内存中,读写性能极高(10万+/秒QPS)。持久化支持:支持RDB(快照)和AOF(追加日志)两种持久化方式。多数据结构:支持字符串、
- 什么是 Redis
yqcoder
redis数据库缓存
Redis(RemoteDictionaryServer)是一个开源的、基于内存的键值存储系统,常用作数据库、缓存和消息中间件。它支持多种数据结构,如字符串、哈希、列表、集合、有序集合等,并提供丰富的操作命令。主要特点高性能:数据存储在内存中,读写速度极快。持久化:支持RDB和AOF两种方式,确保数据在重启后不丢失。数据结构丰富:支持字符串、哈希、列表、集合、有序集合等多种类型。原子操作:所有操作
- C++中map和set的详解
yang789022
c++算法开发语言
C++中map和set的介绍与使用在C++编程中,map和set是标准模板库(STL)中两种非常重要的关联容器。它们基于平衡二叉搜索树(通常是红黑树)的数据结构来实现,提供了高效的数据存储和检索功能。本文将详细介绍map和set的特点、用法以及一些常见的操作示例。一、map的介绍与使用1.map的基本概念map是一个键值对容器,其中每个键都是唯一的,且按照升序排序。map的内部结构是红黑树,这使得
- 深入理解Java集合框架:构建高效、灵活的数据管理方案
love729234ming
java开发语言
深入理解Java集合框架:构建高效、灵活的数据管理方案引言Java集合框架(JavaCollectionsFramework,JCF)是Java语言提供的一套用于表示和操作集合的统一架构。它包含了一系列的接口和类,用于存储和操作对象集合,如列表(List)、集合(Set)、映射(Map)和队列(Queue)等。集合框架的设计初衷是为了提供一套灵活、可重用且类型安全的集合数据结构,帮助开发者以统一和
- C++中map和set的详解
漏洞猎人001
c++算法开发语言
C++中map和set的介绍与使用在C++编程中,map和set是标准模板库(STL)中两种非常重要的关联容器。它们基于平衡二叉搜索树(通常是红黑树)的数据结构来实现,提供了高效的数据存储和检索功能。本文将详细介绍map和set的特点、用法以及一些常见的操作示例。一、map的介绍与使用1.map的基本概念map是一个键值对容器,其中每个键都是唯一的,且按照升序排序。map的内部结构是红黑树,这使得
- Go channel底层实现原理以及为什么要懂原理
Amber_37
Golanggolang
Gochannel底层实现原理Go语言中的channel是一种用于goroutine之间通信和同步的核心机制,其底层实现基于高效的数据结构和调度策略。以下是其底层实现原理的详细分析:1.数据结构:hchanchannel的底层由runtime.hchan结构体表示,包含以下关键字段:buf:指向环形缓冲区的指针,用于存储元素(仅限带缓冲channel)。qcount:当前缓冲区中的元素数量。dat
- 深入理解Java集合框架:构建高效、灵活的数据管理方案
星河浪人
java开发语言
深入理解Java集合框架:构建高效、灵活的数据管理方案引言Java集合框架(JavaCollectionsFramework,JCF)是Java语言提供的一套用于表示和操作集合的统一架构。它包含了一系列的接口和类,用于存储和操作对象集合,如列表(List)、集合(Set)、映射(Map)和队列(Queue)等。集合框架的设计初衷是为了提供一套灵活、可重用且类型安全的集合数据结构,帮助开发者以统一和
- C语言数据结构——变长数组(柔性数组)
Iawfy22
数据结构c语言柔性数组
前言这是一位即将大二的大学生(卷狗)在暑假预习数据结构时的一些学习笔记,供大家参考学习。水平有限,如有错误,还望多多指正。本文主要介绍了如何手动实现一个变长数组,以及实现其部分功能(如删除、查找、添加、排序等)变长数组介绍变长数组又可以叫柔性数组,与一般数组不同,它是一个动态的数组,具体表现为可以根据数组里面元素个数的多少而自动的进行扩容,以便达到变长(柔性)的特点。预备知识为了实现自动边长扩容这
- 王道数据结构第三章(二)- 栈和队列的应用
int型码农
数据结构算法
王道数据结构第三章(二)栈和队列的应用一、栈在括号匹配中的应用1.括号匹配2.实现2.前、中、后缀表达式二、栈在表达式求值中的应用1.后缀表达式(重要)1.1中缀转后缀1.2后缀表达式的计算1.2.1手算1.2.2机算2.前缀表达式2.1中缀转前缀2.2前缀表达式的计算3.中缀表达式3.1中缀转后缀的机算(用栈实现)3.2中缀表达式的计算三、栈在递归中的应用1.阶乘2.斐波那契数列四、队列的应用总
- 【Python】全局解释器锁(Global Interpreter Lock,GIL)
彬彬侠
Python基础全局解释器锁GILCPython多进程C扩展python
全局解释器锁(GlobalInterpreterLock,简称GIL)是CPython(Python的标准实现)中的一个机制,它确保同一时刻只有一个线程在执行Python字节码。GIL的主要作用是保护Python内部的数据结构,避免多线程访问共享数据时发生竞争条件,导致数据损坏。GIL的工作原理在Python的多线程环境中,GIL会限制多个线程同时执行Python字节码。尽管操作系统可以调度多个线
- C# Dictionary使用详解
Daniel的万事通杂货铺
Winform应用开发c#开发语言
在C#中,Dictionary是一个非常常用的数据结构,用于存储键值对。Dictionary类实现了IDictionary接口,并且提供了许多有用的方法和属性来操作键值对集合。下面是一些关于如何使用Dictionary的详细说明:1.基本用法创建DictionaryCsharp深色版本1DictionarymyDictionary=newDictionary();或者使用字面量语法:Csharp深
- 掌握Rust模式匹配:从基础语法到实际应用
GTokenTool发币平台
rust开发语言后端
本篇文章将探讨Rust编程语言中至关重要的特性之一——模式匹配。Rust语言的模式匹配功能强大,不仅能处理简单的值匹配,还能解构和操作复杂的数据结构。通过深入学习模式匹配,程序员可以更加高效地编写出清晰、简洁且易于维护的代码。Rust语言中的模式匹配是一种特殊的语法结构,用于匹配变量、解构数组、结构体、枚举和元组等。本文主要介绍了Rust中各种模式的使用场景,包括match、iflet、while
- 为什么程序员需要学习数字电路
Vitalia
理论基础程序人生学习开发语言数字电路
在编程的世界里,我们通常关注的是算法、数据结构、框架和设计模式等软件层面的知识。然而,数字电路作为计算机硬件的核心基础,对程序员来说同样重要。掌握数字电路不仅能帮助我们更好地理解计算机的底层原理,还能在实际开发中解决一些棘手的问题。本文将通过理论和实例,探讨程序员学习数字电路的必要性。1.数字电路与计算机的关系计算机的核心是中央处理器(CPU),而CPU的本质是由大量的数字电路组成的。数字电路通过
- 数据分析及人工智能框架汇总
xihuanyuye
机器学习
一、数据分析二、人工智能1、Tensorflow1、简介TensorFlow是谷歌基于DistBelief进行研发的第二代人工智能学习系统,其命名来源于本身的运行原理。Tensor(张量)意味着N维数组,Flow(流)意味着基于数据流图的计算,TensorFlow为张量从流图的一端流动到另一端计算过程。TensorFlow是将复杂的数据结构传输至人工智能神经网中进行分析和处理过程的系统。Tenso
- 「QT」布局类 之 QHBoxLayout 水平布局类
何曾参静谧
「QT」QT5程序设计qt开发语言
✨博客主页何曾参静谧的博客(✅关注、点赞、⭐收藏、转发)文章专栏「QT」QT5程序设计全部专栏(专栏会有变化,以最新发布为准)「Win」Windows程序设计「IDE」集成开发环境「UG/NX」BlockUI集合「C/C++」C/C++程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「UG/NX」NX定制开发「Py」Python程序设计「Ma
- C# -Dictionary、HashTable、List、HashSet区别
※※冰馨※※
c#开发语言
在.Net模仿java的过程中,抛弃了HashMap,所以我们今天分析下Dictionary、HashTable、HashSet区别。处理碰撞,即碰撞到同一个Bucket槽上:Hashtable和Dictionary从数据结构上来说都属于Hashtable(哈希表),都是对关键字(键值)进行散列操作,将关键字散列到Hashtable的某一个槽位中去,不同的是处理碰撞的方法。散列函数有可能将不同的关
- 为什么Redis对大 Key(Large Key)和大对象不友好?怎样优化?
风一样的树懒
redis数据库缓存
你好,我是风一样的树懒,一个工作十多年的后端专家,曾就职京东、阿里等多家互联网头部企业。公众号“吴计可师”,已经更新了近百篇高质量的面试相关文章,喜欢的朋友欢迎关注点赞Redis对大Key(LargeKey)和大对象不友好,主要源于其内存管理模型、单线程架构和数据结构特性。以下从性能影响、内存管理、集群限制三个维度解析原因,并提供优化方案:一、Redis对大Key不友好的核心原因1.性能瓶颈单线程
- 存储和访问节点属性 python networkx
潮易
python开发语言
存储和访问节点属性pythonnetworkx在Python中,我们可以使用NetworkX库来创建和管理图数据结构。在NetworkX中,节点可以有属性,例如标签、颜色或价值等。以下是如何存储和访问节点的属性的步骤:1.首先,我们需要导入NetworkX库并创建一个图形对象。然后,我们可以给节点添加属性。```pythonimportnetworkxasnx#创建一个图形对象G=nx.Graph
- Redis五种用途
egekm_sefg
面试学习路线阿里巴巴redis数据库缓存
简介Redis是一个高性能的key-value数据库。Redis与其他key-value缓存产品有以下三个特点:-Redis支持数据的持久化,可以将内存中的数据保存在磁盘中,重启的时候可以再次加载进行使用。-Redis不仅仅支持简单的key-value类型的数据,同时还提供list,set,zset,hash等数据结构的存储。-Redis支持数据的备份,即master-slave模式的数据备份。五
- ES6(4) Map 集合详解
Theodore_1022
ES6es6前端ecmascriptjavascript开发语言
1.Map集合简介Map是ES6提供的一种新的键值对数据结构,与普通对象(Object)不同,Map的键可以是任意类型(包括对象、函数等)。2.创建Map集合可以使用newMap()创建一个Map,并在括号内传入一个二维数组来初始化键值对。letauthor=newMap([['name','theodore'],['age','21'],['web','https://blog.csdn.net
- 蓝桥杯常见算法模板(Python组)
-777.
蓝桥杯算法
目录1.二分1.整数二分(二分答案):2.浮点数二分(考不到)2.前缀和、差分1.前缀和一维:二维:2.差分一维:二维:3.贪心4.线性DP1.最长上升子序列(子序列问题一般下标从一开始)2.最长公共子序列3.常见背包模型1.0-1背包2.完全背包3.多重背包4.混合背包5.二维费用背包6.分组背包5.搜索1.DFS模板:1.子集问题2.全排列问题2.BFS6.数据结构1.并查集2.树状数组3.树
- MongoDB在Spring商城用户行为记录中的应用
小小初霁
mongodbspring数据库
一、MongoDB的优势灵活Schema用户行为数据结构多变(如点击、搜索、下单),MongoDB的文档模型无需固定字段,适应快速迭代。高吞吐写入支持批量插入,适合高并发场景(如秒杀活动的用户操作记录)。复杂查询优化支持聚合管道、地理空间查询、全文索引,便于多维分析。水平扩展通过分片(Sharding)应对海量数据存储。二、用户行为数据建模1.基础行为记录集合(如user_actions){"us
- 搞定leetcode面试经典150题之链表
醒了就刷牙
LeetCode刷题leetcode面试链表
系列博客目录文章目录系列博客目录理论知识单向链表双向链表例题206.反转链表92.反转链表II27.回文链表141.环形链表21.合并有序链表2.两数相加19.删除链表的倒数第N个结点138.随机链表的复制82.删除排序链表中的重复元素II61.旋转链表86.分隔链表理论知识链表是数据结构中一种非常常见且基础的结构,在Java中,链表被广泛应用于解决动态数据存储问题。与数组不同,链表的元素(节点)
- Python中存储数据——json模块
小白的高手之路
python学习pythonjson开发语言
很多时候,程序要把信息存储在列表和字典等数据结构中。一种简单的方式是使用json模块来存储数据。json模块能够将简单的Python数据结构存储到文件中,并在程序运行时加载文件中的数据。还可以使用json在Python程序之间分享数据。更重要的是,JSON数据格式并非Python专用的,能够将以JSON格式存储的数据与使用其他编程语言的人分享。JSON(JavaScriptObjectNotion
- redis在SpringBoot中的使用
小野喵喵。
redisspringboot数据库
以下部分内容由AI生成,再添加自己的理解,仅供参考与了解记录一、redis简单介绍Redis是一个开源的高性能键值对数据库,支持多种数据结构,如字符串(String)、哈希(Hash)、列表(List)、集合(Set)和有序集合(SortedSet)等。核心原理1.单线程模型redis使用单线程处理命令(核心逻辑),避免了多线程竞争问题。通过非阻塞I/O多路复用监听多个客户端连接,高效处理请求。所
- Spring4.1新特性——Spring MVC增强
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- mysql 性能查询优化
annan211
javasql优化mysql应用服务器
1 时间到底花在哪了?
mysql在执行查询的时候需要执行一系列的子任务,这些子任务包含了整个查询周期最重要的阶段,这其中包含了大量为了
检索数据列到存储引擎的调用以及调用后的数据处理,包括排序、分组等。在完成这些任务的时候,查询需要在不同的地方
花费时间,包括网络、cpu计算、生成统计信息和执行计划、锁等待等。尤其是向底层存储引擎检索数据的调用操作。这些调用需要在内存操
- windows系统配置
cherishLC
windows
删除Hiberfil.sys :使用命令powercfg -h off 关闭休眠功能即可:
http://jingyan.baidu.com/article/f3ad7d0fc0992e09c2345b51.html
类似的还有pagefile.sys
msconfig 配置启动项
shutdown 定时关机
ipconfig 查看网络配置
ipconfig /flushdns
- 人体的排毒时间
Array_06
工作
========================
|| 人体的排毒时间是什么时候?||
========================
转载于:
http://zhidao.baidu.com/link?url=ibaGlicVslAQhVdWWVevU4TMjhiKaNBWCpZ1NS6igCQ78EkNJZFsEjCjl3T5EdXU9SaPg04bh8MbY1bR
- ZooKeeper
cugfy
zookeeper
Zookeeper是一个高性能,分布式的,开源分布式应用协调服务。它提供了简单原始的功能,分布式应用可以基于它实现更高级的服务,比如同步, 配置管理,集群管理,名空间。它被设计为易于编程,使用文件系统目录树作为数据模型。服务端跑在java上,提供java和C的客户端API。 Zookeeper是Google的Chubby一个开源的实现,是高有效和可靠的协同工作系统,Zookeeper能够用来lea
- 网络爬虫的乱码处理
随意而生
爬虫网络
下边简单总结下关于网络爬虫的乱码处理。注意,这里不仅是中文乱码,还包括一些如日文、韩文 、俄文、藏文之类的乱码处理,因为他们的解决方式 是一致的,故在此统一说明。 网络爬虫,有两种选择,一是选择nutch、hetriex,二是自写爬虫,两者在处理乱码时,原理是一致的,但前者处理乱码时,要看懂源码后进行修改才可以,所以要废劲一些;而后者更自由方便,可以在编码处理
- Xcode常用快捷键
张亚雄
xcode
一、总结的常用命令:
隐藏xcode command+h
退出xcode command+q
关闭窗口 command+w
关闭所有窗口 command+option+w
关闭当前
- mongoDB索引操作
adminjun
mongodb索引
一、索引基础: MongoDB的索引几乎与传统的关系型数据库一模一样,这其中也包括一些基本的优化技巧。下面是创建索引的命令: > db.test.ensureIndex({"username":1}) 可以通过下面的名称查看索引是否已经成功建立: &nbs
- 成都软件园实习那些话
aijuans
成都 软件园 实习
无聊之中,翻了一下日志,发现上一篇经历是很久以前的事了,悔过~~
断断续续离开了学校快一年了,习惯了那里一天天的幼稚、成长的环境,到这里有点与世隔绝的感觉。不过还好,那是刚到这里时的想法,现在感觉在这挺好,不管怎么样,最要感谢的还是老师能给这么好的一次催化成长的机会,在这里确实看到了好多好多能想到或想不到的东西。
都说在外面和学校相比最明显的差距就是与人相处比较困难,因为在外面每个人都
- Linux下FTP服务器安装及配置
ayaoxinchao
linuxFTP服务器vsftp
检测是否安装了FTP
[root@localhost ~]# rpm -q vsftpd
如果未安装:package vsftpd is not installed 安装了则显示:vsftpd-2.0.5-28.el5累死的版本信息
安装FTP
运行yum install vsftpd命令,如[root@localhost ~]# yum install vsf
- 使用mongo-java-driver获取文档id和查找文档
BigBird2012
driver
注:本文所有代码都使用的mongo-java-driver实现。
在MongoDB中,一个集合(collection)在概念上就类似我们SQL数据库中的表(Table),这个集合包含了一系列文档(document)。一个DBObject对象表示我们想添加到集合(collection)中的一个文档(document),MongoDB会自动为我们创建的每个文档添加一个id,这个id在
- JSONObject以及json串
bijian1013
jsonJSONObject
一.JAR包简介
要使程序可以运行必须引入JSON-lib包,JSON-lib包同时依赖于以下的JAR包:
1.commons-lang-2.0.jar
2.commons-beanutils-1.7.0.jar
3.commons-collections-3.1.jar
&n
- [Zookeeper学习笔记之三]Zookeeper实例创建和会话建立的异步特性
bit1129
zookeeper
为了说明问题,看个简单的代码,
import org.apache.zookeeper.*;
import java.io.IOException;
import java.util.concurrent.CountDownLatch;
import java.util.concurrent.ThreadLocal
- 【Scala十二】Scala核心六:Trait
bit1129
scala
Traits are a fundamental unit of code reuse in Scala. A trait encapsulates method and field definitions, which can then be reused by mixing them into classes. Unlike class inheritance, in which each c
- weblogic version 10.3破解
ronin47
weblogic
版本:WebLogic Server 10.3
说明:%DOMAIN_HOME%:指WebLogic Server 域(Domain)目录
例如我的做测试的域的根目录 DOMAIN_HOME=D:/Weblogic/Middleware/user_projects/domains/base_domain
1.为了保证操作安全,备份%DOMAIN_HOME%/security/Defa
- 求第n个斐波那契数
BrokenDreams
今天看到群友发的一个问题:写一个小程序打印第n个斐波那契数。
自己试了下,搞了好久。。。基础要加强了。
&nbs
- 读《研磨设计模式》-代码笔记-访问者模式-Visitor
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
interface IVisitor {
//第二次分派,Visitor调用Element
void visitConcret
- MatConvNet的excise 3改为网络配置文件形式
cherishLC
matlab
MatConvNet为vlFeat作者写的matlab下的卷积神经网络工具包,可以使用GPU。
主页:
http://www.vlfeat.org/matconvnet/
教程:
http://www.robots.ox.ac.uk/~vgg/practicals/cnn/index.html
注意:需要下载新版的MatConvNet替换掉教程中工具包中的matconvnet:
http
- ZK Timeout再讨论
chenchao051
zookeepertimeouthbase
http://crazyjvm.iteye.com/blog/1693757 文中提到相关超时问题,但是又出现了一个问题,我把min和max都设置成了180000,但是仍然出现了以下的异常信息:
Client session timed out, have not heard from server in 154339ms for sessionid 0x13a3f7732340003
- CASE WHEN 用法介绍
daizj
sqlgroup bycase when
CASE WHEN 用法介绍
1. CASE WHEN 表达式有两种形式
--简单Case函数
CASE sex
WHEN '1' THEN '男'
WHEN '2' THEN '女'
ELSE '其他' END
--Case搜索函数
CASE
WHEN sex = '1' THEN
- PHP技巧汇总:提高PHP性能的53个技巧
dcj3sjt126com
PHP
PHP技巧汇总:提高PHP性能的53个技巧 用单引号代替双引号来包含字符串,这样做会更快一些。因为PHP会在双引号包围的字符串中搜寻变量, 单引号则不会,注意:只有echo能这么做,它是一种可以把多个字符串当作参数的函数译注: PHP手册中说echo是语言结构,不是真正的函数,故把函数加上了双引号)。 1、如果能将类的方法定义成static,就尽量定义成static,它的速度会提升将近4倍
- Yii框架中CGridView的使用方法以及详细示例
dcj3sjt126com
yii
CGridView显示一个数据项的列表中的一个表。
表中的每一行代表一个数据项的数据,和一个列通常代表一个属性的物品(一些列可能对应于复杂的表达式的属性或静态文本)。 CGridView既支持排序和分页的数据项。排序和分页可以在AJAX模式或正常的页面请求。使用CGridView的一个好处是,当用户浏览器禁用JavaScript,排序和分页自动退化普通页面请求和仍然正常运行。
实例代码如下:
- Maven项目打包成可执行Jar文件
dyy_gusi
assembly
Maven项目打包成可执行Jar文件
在使用Maven完成项目以后,如果是需要打包成可执行的Jar文件,我们通过eclipse的导出很麻烦,还得指定入口文件的位置,还得说明依赖的jar包,既然都使用Maven了,很重要的一个目的就是让这些繁琐的操作简单。我们可以通过插件完成这项工作,使用assembly插件。具体使用方式如下:
1、在项目中加入插件的依赖:
<plugin>
- php常见错误
geeksun
PHP
1. kevent() reported that connect() failed (61: Connection refused) while connecting to upstream, client: 127.0.0.1, server: localhost, request: "GET / HTTP/1.1", upstream: "fastc
- 修改linux的用户名
hongtoushizi
linuxchange password
Change Linux Username
更改Linux用户名,需要修改4个系统的文件:
/etc/passwd
/etc/shadow
/etc/group
/etc/gshadow
古老/传统的方法是使用vi去直接修改,但是这有安全隐患(具体可自己搜一下),所以后来改成使用这些命令去代替:
vipw
vipw -s
vigr
vigr -s
具体的操作顺
- 第五章 常用Lua开发库1-redis、mysql、http客户端
jinnianshilongnian
nginxlua
对于开发来说需要有好的生态开发库来辅助我们快速开发,而Lua中也有大多数我们需要的第三方开发库如Redis、Memcached、Mysql、Http客户端、JSON、模板引擎等。
一些常见的Lua库可以在github上搜索,https://github.com/search?utf8=%E2%9C%93&q=lua+resty。
Redis客户端
lua-resty-r
- zkClient 监控机制实现
liyonghui160com
zkClient 监控机制实现
直接使用zk的api实现业务功能比较繁琐。因为要处理session loss,session expire等异常,在发生这些异常后进行重连。又因为ZK的watcher是一次性的,如果要基于wather实现发布/订阅模式,还要自己包装一下,将一次性订阅包装成持久订阅。另外如果要使用抽象级别更高的功能,比如分布式锁,leader选举
- 在Mysql 众多表中查找一个表名或者字段名的 SQL 语句
pda158
mysql
在Mysql 众多表中查找一个表名或者字段名的 SQL 语句:
方法一:SELECT table_name, column_name from information_schema.columns WHERE column_name LIKE 'Name';
方法二:SELECT column_name from information_schema.colum
- 程序员对英语的依赖
Smile.zeng
英语程序猿
1、程序员最基本的技能,至少要能写得出代码,当我们还在为建立类的时候思考用什么单词发牢骚的时候,英语与别人的差距就直接表现出来咯。
2、程序员最起码能认识开发工具里的英语单词,不然怎么知道使用这些开发工具。
3、进阶一点,就是能读懂别人的代码,有利于我们学习人家的思路和技术。
4、写的程序至少能有一定的可读性,至少要人别人能懂吧...
以上一些问题,充分说明了英语对程序猿的重要性。骚年
- Oracle学习笔记(8) 使用PLSQL编写触发器
vipbooks
oraclesql编程活动Access
时间过得真快啊,转眼就到了Oracle学习笔记的最后个章节了,通过前面七章的学习大家应该对Oracle编程有了一定了了解了吧,这东东如果一段时间不用很快就会忘记了,所以我会把自己学习过的东西做好详细的笔记,用到的时候可以随时查找,马上上手!希望这些笔记能对大家有些帮助!
这是第八章的学习笔记,学习完第七章的子程序和包之后