十大排序算法详解(二)归并排序、堆排序、计数排序、桶排序、基数排序
文章目录
-
- 一、归并排序
-
- 1.1 归并排序基础【必会知识】
-
- 1.1.1 递归实现
- 1.1.2 非递归实现
- 1.2 归并排序优化
-
- 1.2.1 小数组使用插入排序
- 1.2.2 避免多余比较
- 1.2.3 节省元素拷贝时间
- 1.3 归并排序的稳定性、复杂度及适用场景
-
- 1.3.1 稳定性
- 1.3.2 时间复杂度
- 1.3.3 适用场景
- 二、堆排序
-
- 2.1 堆排序基础
- 2.2 堆排序的稳定性、复杂度及适用场景
-
- 2.2.1 稳定性
- 2.2.2 时间复杂度
- 2.2.3 适用场景
- 三、计数排序
-
- 3.1 计数排序基础
-
- 3.1.1 计数排序图示
- 3.1.2 计数排序实现
- 3.2 计数排序优化
-
- 3.2.1 控制索引数组下表起始位置
- 3.2.2 如何达到稳定效果
- 3.3 计数排序的稳定性、复杂度及适用场景
-
- 3.3.1 稳定性
- 3.3.2 复杂度
- 3.3.3 适用场景
- 四、桶排序
-
- 4.1 桶排序基础
-
- 4.1.1 桶排序图示
- 4.1.2 桶排序实现
- 4.2 桶排序的稳定性、复杂度及适用场景
-
- 4.2.1 稳定性
- 4.2.2 复杂度
- 4.2.3 适用场景
- 五、基数排序
-
- 5.1 基数排序基础
-
- 5.1.1 基数排序图示
- 5.1.2 基数排序实现
- 5.2 基数排序优化
- 5.3 基数排序的稳定性、复杂度及适用场景
-
- 5.3.1 稳定性
- 5.3.2 复杂度
- 5.3.3 适用场景
一、归并排序
1.1 归并排序基础【必会知识】
1.1.1 递归实现
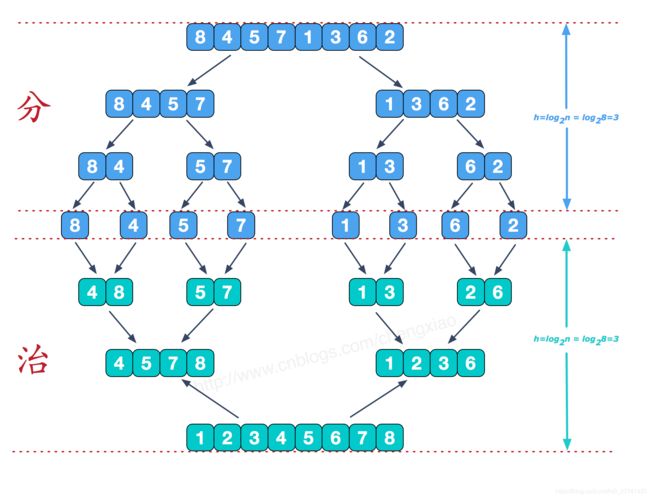
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序是一种稳定的排序方法。
归并排序的步骤:
1>创建临时数组,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
2>设定两个指针,最初位置分别为两个已经排序序列的起始位置;
3>比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
4>重复步骤 3 直到某一指针达到序列尾;
5>将另一序列剩下的所有元素直接复制到合并序列尾。
将上述过程用代码表示,示例如下:
// 递归方法实现
public static void mergeSort1(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr, 0, arr.length - 1);
}
//该方法表示将arr数组的L到R位置上的数字变为有序的
public static void process(int[] arr, int L, int R) {
//俗称base case,即划分到什么程度时,就不需要再继续划分了
if (L == R) {
return;
}
//求中间位置,L到mid是左侧递归部分的数据,mid+1到R是右侧递归部分的数据
int mid = L + ((R - L) >> 1);
//左右两侧进行递归拆分
process(arr, L, mid);
process(arr, mid + 1, R);
//再将arr中的左右两部分合并为有序的,L到mid为左侧部分,mid+1到R是右侧
//递归部分的数据,所以位置信息传三个参数就行,不用传mid+1参数
merge(arr, L, mid, R);
}
//
public static void merge(int[] arr, int L, int M, int R) {
//准备辅助数组,存放排序后的数据
int[] help = new int[R - L + 1];
int i = 0;
//左侧数据起始位置
int p1 = L;
//右侧数据起始位置
int p2 = M + 1;
//左右两侧都没遍历完,即p1、p2都没越界
while (p1 <= M && p2 <= R) {
//将左右部分的数据进行比较,小的数据存放到辅助数组,
//然后help和添加到辅助数组的部分指针(p1或p2)进行右移
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
//当跳出wile循环,代表左或右某个部分已经遍历完了,然后将未
//遍历完的追加到辅助数组尾部,下面的两个while循环只能有一个执行
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
//将辅助数组中的数据追加到原arr数组中
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
}
递归方式的时间复杂度为:T(N) = 2 * T(N/2) + O(N1),即最终的结果为:O(N * logN)。
1.1.2 非递归实现
// 非递归方法实现
public static void mergeSort2(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
int N = arr.length;
//mergeSize代表每次合并时,一半(可以理解为左侧)数据量的大小
int mergeSize = 1;
while (mergeSize < N) {
int L = 0;
while (L < N) {
//从L到M位置的数据就是当前合并部分的左侧数据大小,数据量为mergeSize
int M = L + mergeSize - 1;
//表示当前要合并的数据量凑不够本次合并的左侧部分,比如本次要合并的数据量
//为8,则左侧数据量为4,但剩余未合并的数只有3个了,则这三个本次不用再
//合并,因为这三个数肯定在上次合并时已经有序了
if (M >= N) {
break;
}
//上面的过程是寻找左侧数据的过程,即:L...M,接下来要找右侧数据。此时
//就要分情况了。为什么呢?正常情况下右侧数据的边界是从M+1到M + mergeSize,
//但有可能右侧没这么多数据了,右边界实际是N-1,所以右边界应该取这两个
//数的最小值(其实就代表实际值)
int R = Math.min(M + mergeSize, N - 1);
//分出了左右边界,接下来就是进行合并了
merge(arr, L, M, R);
L = R + 1;
}
//此处的if语句算一个优化语句,不影响功能,防止的是:mergeSize在*2的过程
//中超过Integer.MAX_VALUE,出现错误
if (mergeSize > N / 2) {
break;
}
//每次合并扩大一倍
mergeSize = mergeSize * 2;
}
}
非递归方式的时间复杂度也是O(N * logN),因为每次合并的时间复杂度为O(N),进行了logN次合并过程。
1.2 归并排序优化
归并排序常用的优化方式有3种:
- 对于小数组可以使用插入排序或者选择排序,避免递归调用。
- 在合并两个子数组之前,可以比较左边子数组的最后一个值是否小于右边子数组的第一个值,如果小于,则不用再逐个比较左右子数组的元素,因为左右子数组都已有序,直接合并就行。
- 为了节省将元素复制到辅助数组作用的时间,可以在递归调用的每个层次交换原始数组与辅助数组的角色。
1.2.1 小数组使用插入排序
该种优化方式比较容易理解,实现方式为在mergeArray方法的开始位置,加入对子数组的数量判断即可,示例代码如下:
/*优化方式1:对于小序列,使用插入排序,比如小序列数量<=7时*/
if((end-start) >= 7){
insertionSort(arr,end-start);
}
1.2.2 避免多余比较
第二种优化,针对的是某一子数组已经有序,并且完全大于(小于)另一子数组,在本次合并时,则不需要再对该有序子序列中的元素挨个进行比较的情况,此时,直接返回即可。
我们可以先将初始的数组改成{4,2,3,5,7,9},然后在mergeArray的while循环中,加入一些语句,打印一下当时的子数组中的元素,示例如下:
while(i<=m && j<=n){
System.out.print("arr["+i+"]:"+arr[i]+",arr["+j+"]:"+arr[j]);
System.out.println();
/*左右,哪个子序列的数据小,就放入临时数组temp*/
if(arr[i]<arr[j])
temp[k++] = arr[i++];
else
temp[k++] = arr[j++];
}
此时,打印结果如下:
arr[0]:4,arr[1]:2
arr[0]:2,arr[2]:3
arr[1]:4,arr[2]:3
arr[3]:5,arr[4]:7
arr[3]:5,arr[5]:9
arr[4]:7,arr[5]:9
arr[0]:2,arr[3]:5
arr[1]:3,arr[3]:5
arr[2]:4,arr[3]:5
从上面的打印可以看出,数组的后三个元素组成的子数组是{5,7,9},即有序后,还是在和前面的{2,3,4}挨个比较,这个过程完全没用必要,可以规避掉。这也是此种优化方式的目的,示例代码如下:
public static void main(String[] args) {
int[ ] array = new int[ ]{4,2,3,5,7,9};
int[ ] temp = new int[6];
/*借助temp数组对array数组中的0 - array.length-1位置的元素进行排序*/
mergeSort(array,0,array.length-1,temp);
System.out.println("排序后的结果:");
for(int i = 0;i<array.length;i++)
System.out.print(array[i]+" ");
}
static void mergeSort(int arr[],int start,int end,int temp[]){
if(start<end){
int mid = (start+end)/2;
/*拆分左右序列*/
mergeSort(arr,start,mid,temp);
mergeSort(arr,mid+1,end,temp);
/*将每个拆分的序列进行合并*/
mergeArray(arr,start,mid,end,temp);
}
}
/*将两个数组归并排序*/
static void mergeArray(int arr[],int start,int mid,int end,int temp[]) {
/*将每个子序列,即arr[start] - arr[end],拆分成左右两部分:下标i到m为左部分,
*下标j到n为右部分
*/
int i = start,j = mid+1;
int m = mid,n = end;
/*k代表临时数组元素的下标*/
int k = 0;
if(arr[mid]<arr[mid+1]){
return;
}
/*左右两个子序列都有元素*/
while(i<=m && j<=n){
System.out.print("arr["+i+"]:"+arr[i]+",arr["+j+"]:"+arr[j]);
System.out.println();
/*左右,哪个子序列的数据小,就放入临时数组temp*/
if(arr[i]<arr[j])
temp[k++] = arr[i++];
else
temp[k++] = arr[j++];
}
/*左边序列还有数据,直接追加到temp数组中*/
while(i<=m)
temp[k++] = arr[i++];
/*右边序列还有数据,直接追加到temp数组中*/
while(j<=n)
temp[k++] = arr[j++];
/*将临时数组temp的元素追加在原数组arr中*/
for(i=0;i<k;i++)
arr[start+i] = temp[i];
}
测试结果如下:
arr[0]:4,arr[1]:2
arr[0]:2,arr[2]:3
arr[1]:4,arr[2]:3
排序后的结果:
2 3 4 5 7 9
1.2.3 节省元素拷贝时间
此种优化,是想节省在原数组和辅助数组之间拷贝元素的时间,做法是:先克隆原数组到辅助数组,然后对克隆出来的辅助数组进行拆,拆完后合并时,替换原有数组中对应位置的元素,示例代码如下:
public static void main(String[] args) {
int[ ] array = new int[ ]{4,2,3,5,7,9,8};
/*拷贝一个和a所有元素相同的辅助数组*/
int[] arrTemp = array.clone();
sort(array,arrTemp,0,array.length-1);
System.out.println("排序后的结果:");
for(int i = 0;i<array.length;i++)
System.out.print(array[i]+" ");
}
/*基于递归的归并排序算法*/
static void sort (int a[], int temp[], int start,int end) {
if(end > start){
int mid = start+(end-start)/2;
/*对左右子序列递归*/
sort(temp, a,start,mid);
sort(temp, a,mid+1,end);
/*合并左右子数组*/
merge(a, temp, start,mid,end);
}
}
/*arr[low...high] 是待排序序列,其中arr[low...mid]和 a[mid+1...high]已有序*/
static void merge (int arr[],int temp[],int start,int mid,int end) {
/*左边子序列的头元素*/
int i = start;
/*右边子序列的头元素*/
int j = mid+1;
for(int k = start;k <= end;k++){
if(i>mid){
/*左边子序列元素用尽*/
arr[k] = temp[j++];
}else if(j>end){
/*右边子序列元素用尽*/
arr[k] = temp[i++];
}else if(temp[j]<temp[i]){
/*右边子序列当前元素小于左边子序列当前元素, 取右半边元素*/
arr[k] = temp[j++];
}else {
/*右边子序列当前元素大于等于左边子序列当前元素,取左半边元素*/
arr[k] = temp[i++];
}
}
}
1.3 归并排序的稳定性、复杂度及适用场景
1.3.1 稳定性
归并排序是一种稳定的排序算法,因为在拆、合的过程中,如果多个元素相等,不用移动其相对位置,就可完成排序过程。
1.3.2 时间复杂度
因为归并排序使用的是分治的思想,可以简单理解为要进行logN次合并,每次合并的数量级是N,所以其时间复杂度为O(nlogn)。
1.3.3 适用场景
待排序序列中元素较多,并且要求较快的排序速度时。
二、堆排序
2.1 堆排序基础
堆排序是指利用堆这种数据结构所设计的一种排序算法。该排序方式主要利用了堆的一些特点:
1>结构近似于完全二叉树,这样就可以在每层的节点中从左到右遍历。
2>子结点的值总是小于(或者大于)它的父节点,即是一个大顶堆或小顶堆。
2.2 堆排序的稳定性、复杂度及适用场景
2.2.1 稳定性
堆排序是一种不稳定的排序,原因是:在非堆顶元素在向堆顶移动的过程中,经历着堆层次的改变,这就有可能导致相等元素相对位置的改变。因此,堆排序是一种不稳定的排序方式。
2.2.2 时间复杂度
初始化建堆的时间复杂度为O(n),排序重建堆的时间复杂度为nlog(n),所以总的时间复杂度为O(n+nlogn)=O(nlogn)。
2.2.3 适用场景
待排序序列中元素个数较多,此时就可以使用堆排序,因为堆排序效率高。
三、计数排序
3.1 计数排序基础
计数排序不是一个比较排序算法,是一种牺牲空间来换取时间的排序算法,其基本步骤如下:
1>找出原数组中元素值最大的,记为max。
2>创建一个新数组count,其长度是max加1,其元素默认值都为0。
3>遍历原数组中的元素,以原数组中的元素作为count数组的索引,以原数组中的元素出现次数作为count数组的元素值。
4>创建结果数组result,起始索引index。
5>遍历count数组,找出其中元素值大于0的元素,将其对应的索引作为元素值填充到result数组中去,每处理一次,count中的该元素值减1,直到该元素值不大于0,依次处理count中剩下的元素。
6>返回结果数组result。
3.1.1 计数排序图示
以一个{2,4,5,9,6,7,3,4}为例,展现一下上面的计数排序的过程。原始数组为:
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 值 | 2 | 4 | 5 | 9 | 6 | 7 | 3 | 4 |
接下来就需要创建一个计数数组,默认长度为原始数组的个数+1,即9,默认填充元素为0:

然后按照原始数组,依次填充索引数组,过程如下:
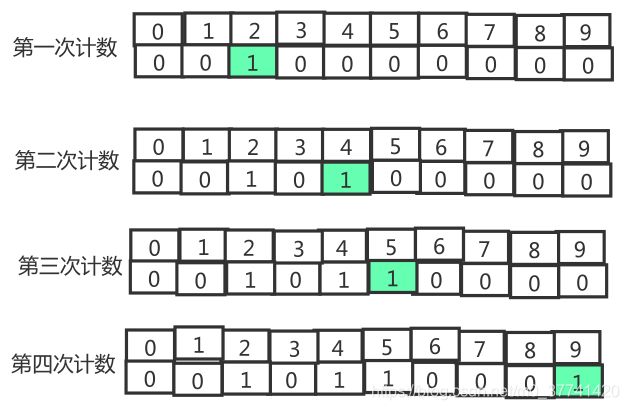
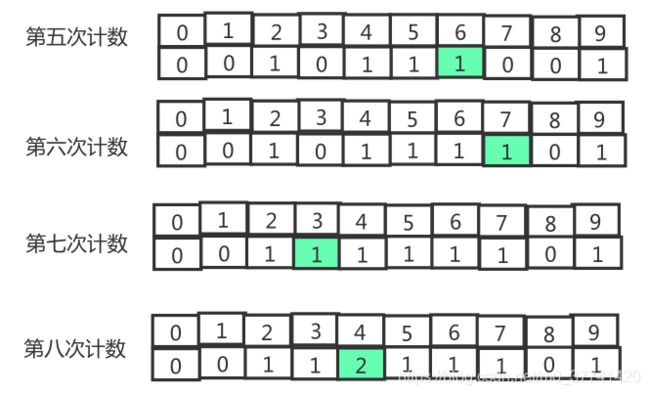
然后就按索引数组,将数据输出到排序后的数组:
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 值 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 9 |
即{2,3,4,4,5,6,7,9}。
3.1.2 计数排序实现
将上述过程,用代码实现,示例为:
static int[] countSort(int[] array) {
/*找出原数组中的最大值*/
int max = 0;
for (int num : array) {
max = Math.max(max, num);
}
/*初始化计数数组count*/
int[ ] count = new int[max+1];
// 对计数数组各元素赋值
for(int num:array){
count[num]++;
}
/*创建结果数组*/
int[ ] result = new int[array.length];
/*创建结果数组的起始索引*/
int index = 0;
/*遍历计数数组,将计数数组的索引填充到结果数组中*/
for(int i = 0; i<count.length; i++){
while(count[i]>0){
result[index++] = i;
count[i]--;
}
}
return result;
}
3.2 计数排序优化
3.2.1 控制索引数组下表起始位置
计数排序有个特点,比较适用于在某个区间内元素排序。这句话翻译一下就是:如果有些元素较大,索引数组中下标从0开始,就会造成计数数组长度很长,但都填充的无效数字0,造成空间浪费。此时,就需要合理控制一下计数数组的下标,进而达到控制计数数组长度的目的,这就是第一种优化方式。
具体的做法是:找出原始数组中的最大值max和最小值min,将计数数组长度定为max-min+1,,根据两者的差来确定计数数组的长度。优化后示例代码如下:
static int[] countSort(int[] array) {
/*找出原始数组中的最大值、最小值*/
int max = 0;
int min = 0;
for (int num : array) {
max = Math.max(max, num);
min = Math.min(min, num);
}
/*初始化计数数组count,长度为最大值减最小值加1*/
int[ ] count = new int[max-min+1];
// 对计数数组各元素赋值
for (int num : array) {
/*原数组array中的元素要减去最小值,再作为新索引*/
count[num-min]++;
}
/*创建结果数组*/
int[] result = new int[array.length];
/*结果数组的起始索引*/
int index = 0;
/*遍历计数数组,将计数数组的索引填充到结果数组中*/
for(int i=0; i<count.length; i++){
while (count[i]>0) {
/*再将减去的最小值补上*/
result[index++] = i+min;
count[i]--;
}
}
return result;
}
3.2.2 如何达到稳定效果
此处的稳定指的是排序前面,相同元素相对位置不变,在上面的两种计数排序中,是不能保证结果的稳定的。如果要保证结果的稳定,此时需要对计数数组变形,如原始的待排序数组为{100,99,100,107},按第一种优化方式,计数数组下标为99、100、101、102、103、104、105、106、107,对应的值为{1,2,0,0,0,0,0,0,1}。这时,需要将计数数组中后面元素的值变成前面元素累加之和的值,此时计数数组的值变为{1,3,3,3,3,3,3,3,4},即:
| 索引 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 |
|---|---|---|---|---|---|---|---|---|---|
| 值 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
然后再从后向前遍历原始数组array,逐个添加到原始数组中去,示例代码如下:
public static void main(String[] args) {
int[ ] array = new int[ ]{100,99,100,107};
int[ ] result = countSort(array);
System.out.println("排序后的数组为:");
for(int i=0;i<array.length;i++)
System.out.print(result[i]+" ");
}
static int[] countSort(int[] array) {
// 找出原始数组array中的最大值、最小值
int max = 0;
int min = 0;
for (int num : array) {
max = Math.max(max, num);
min = Math.min(min, num);
}
/*初始化计数数组count,长度为最大值减最小值加1*/
int[] count = new int[max-min+1];
/*对计数数组各元素赋值*/
for (int num : array) {
/*array中的元素要减去最小值,再作为新索引*/
count[num-min]++;
}
/*计数数组变形,新元素的值是前面元素累加之和的值*/
for (int i=1; i<count.length; i++) {
count[i] += count[i-1];
}
System.out.println("计数数组为:");
for(int i = 0; i<count.length;i++){
if(count[i]>0)
System.out.print("索引["+ i +"]:"+count[i]+"\n");
}
/*结果数组*/
int[] result = new int[array.length];
/*遍历array中的元素,填充到结果数组中去,从后往前遍历*/
for (int j=array.length-1; j>=0; j--) {
/*计数数组下标*/
int countIndex = array[j]-min;
/*结果数组下标*/
int resultIndex = count[countIndex]-1;
System.out.println("计数数组下标为:"+countIndex+",结果数组下标:"+resultIndex+",原始数组下标:"+j);
result[resultIndex] = array[j];
count[countIndex]--;
}
return result;
}
测试结果为:
计数数组为:
索引[99]:1
索引[100]:3
索引[101]:3
索引[102]:3
索引[103]:3
索引[104]:3
索引[105]:3
索引[106]:3
索引[107]:4
计数数组下标为:107,结果数组下标:3,原始数组下标:3
计数数组下标为:100,结果数组下标:2,原始数组下标:2
计数数组下标为:99,结果数组下标:0,原始数组下标:1
计数数组下标为:100,结果数组下标:1,原始数组下标:0
排序后的数组为:
99 100 100 107
3.3 计数排序的稳定性、复杂度及适用场景
3.3.1 稳定性
计数排序是稳定的。
3.3.2 复杂度
计数排序的复杂度是O(n + k),n是输入数组长度,k是最大的数的大小。
3.3.3 适用场景
待排序序列是在一定范围内的整数。
四、桶排序
4.1 桶排序基础
桶排序,即箱排序,其原理是将数组分到有限数量的桶子里,每个桶子再个别排序。其基本步骤如下:
1>先计算装所有元素所需要的桶的个数。
2>将待排序元素按大小装到对应的桶中。
3>对每个桶内的元素进行排序。
4>将所有桶中的元素按顺序放入到原数组中。
4.1.1 桶排序图示
假设原始数组如下:

接下来就要分桶,假如按10个元素一个区间,即一个桶,将元素装到对应的桶中,结果如下:
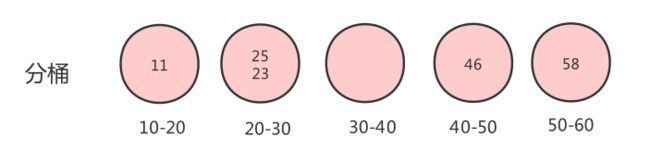
对桶内元素进行排序,结果如下:
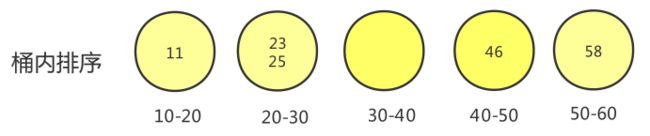
最后将桶内的元素,输出到原始数组,结果如下:

4.1.2 桶排序实现
将上述过程,用代码实现,示例如下:
/*计算最大值与最小值*/
int max = 0;
int min = 0;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
/*计算桶的数量*/
int bucketNum = (max-min)/arr.length+1;
/*用ArrayList组织对应的桶*/
List<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0;i<bucketNum;i++){
bucketArr.add(new ArrayList<Integer>());
}
/*将每个元素放入对应的桶*/
for(int i = 0; i<arr.length;i++){
/*找元素对应的桶*/
int num = (arr[i]-min)/(arr.length);
/*在同种放入对应的元素*/
bucketArr.get(num).add(arr[i]);
}
/*对每个桶内的元素进行排序*/
for(int i = 0; i<bucketArr.size();i++){
Collections.sort(bucketArr.get(i));
}
/*将桶中的元素赋值到原始数组arr*/
for(int i = 0,index = 0; i < bucketArr.size(); i++){
for(int j = 0; j < bucketArr.get(i).size(); j++){
arr[index++] = bucketArr.get(i).get(j);
}
}
4.2 桶排序的稳定性、复杂度及适用场景
4.2.1 稳定性
桶排序其实是分段排序,是一种较笼统的算法概念,是否稳定实质上取决于桶内采用的排序算法。不过从桶与桶之间的元素关系来看是稳定的,所以一般,也认为桶排序是稳定的。
4.2.2 复杂度
N个数据平均的分配到M个桶中,这样每个桶就有[N/M]个数据量。对于N个待排数据,M个桶,平均每个桶[N/M]个数据的桶排序平均时间复杂度为:
O(N)+O(M*(N/M)log(N/M))=O(N+N(logN-logM))=O(N+NlogN-NlogM)
当N=M时,即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。
4.2.3 适用场景
数据均匀分布在一个区间内。
五、基数排序
5.1 基数排序基础
基数排序是一种非比较型整数排序算法,其基本思想是:将整数按位数切割成不同的数字,然后按每个位数分别比较。
基数排序的具体做法是:
1>将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。
2>从最低位开始,依次进行一次排序。
3>依次从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
5.1.1 基数排序图示
以数组[11,54,46,25,23]为例,由于各元素位数相同,所以不用进行补位。先从个位开始进行比较排序,数组变成[11,23,54,25,46]。再按十位进行比较排序,数组变成[11,23,25,46,54],排序完成,图示如下:
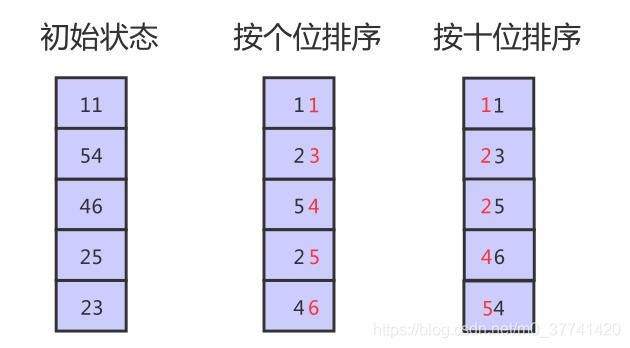
5.1.2 基数排序实现
将上述过程用代码实现,示例为:
static void radixSort(int[] array, int digit) {
/*此处桶数之所以取10,是因为数字0-9总共是十个数字,因此每趟比较时,分为10个桶*/
int radix = 10;
int i = 0, j = 0;
/*存放各个桶的数据统计个数*/
int[] count = new int[radix];
int[] bucket = new int[array.length];
/*按照从低位到高位的顺序执行排序过程*/
for (int d = 1; d <= digit; d++) {
/*置空各个桶的数据统计*/
for (i = 0; i < radix; i++) {
count[i] = 0;
}
/*统计各个桶将要装入的数据个数*/
for (i = 0; i <array.length; i++) {
j = getDigit(array[i], d);
count[j]++;
}
/*count[i]表示第i个桶的右边界索引*/
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
/*将数据依次装入桶中,这里要从右向左扫描,保证排序稳定性*/
for (i = array.length-1; i >= 0; i--) {
j = getDigit(array[i], d);
/*求出元素的第k位的数字, 例如:576的第3位是5*/
bucket[count[j] - 1] = array[i];
/*放入对应的桶中,count[j]-1是第j个桶的右边界索引,对应桶的装入数据索引减一*/
count[j]--; //
}
/*将已分配好的桶中数据再倒出来,此时已是对应当前位数有序的表*/
for (i = 0, j = 0; i < array.length; i++, j++) {
array[i] = bucket[j];
}
}
}
/*获取x这个数的d位数上的数字,比如获取123的1位数,结果返回3*/
static int getDigit(int num, int d) {
/*本实例中的最大数是百位数,所以只要到100就可以了*/
int digit[] = {1, 10, 100};
return ((num/digit[d-1]) % 10);
}
5.2 基数排序优化
基数排序的优化多在于getDigit方法,即获取对应位数的数字上,如常规的该方法实现为:
int getDigit(int n,int i)
{
int p=(int)pow(radix,i);
return (int)(n*p)%radix;
}
pow方法的调用,可能会影响速度,可改为上面示例代码中的实现方法:
static int getDigit(int num, int d) {
int digit[] = {1, 10, 100};
return ((num/digit[d-1]) % 10);
}
5.3 基数排序的稳定性、复杂度及适用场景
5.3.1 稳定性
基数排序是稳定的排序方法。
5.3.2 复杂度
在基数排序中,r为基数,d为位数。则基数排序的时间复杂度为O(d(n+r))。
5.3.3 适用场景
基数排序的适用场景和计数排序类似,即待排序序列是在一定范围内的整数。