(王道408考研数据结构)第五章树-第四节2：平衡二叉树(AVL)及其旋转

一：AVL树基本概念

二叉排序树有一个缺陷：树的高度会直接影响其查找效率，且树越高效率越差，效率最差时为一棵单分支树

平衡二叉树(Self-Balancing Binary Search Tree)：它首先是一颗二叉排序树，其中每个节点的左右子树高度之差绝对值不超过1。将二叉树上结点左子树和右子树高度之差的绝对值称之为平衡因子BF(Balance Factor)，因此，平衡因子BF的取值只可能是-1、0和1中的一种

• -1：表示该结点左子树高度小于右子树高度
• 0：表示该结点左子树高度等于右子树高度
• 1：表示该结点左子树高度大于右子树高度

以下是一些例子

• ①是AVL树
• ②不是AVL树，因为AVL树前提必须首先是二叉排序树
• ③不是AVL树，因为结点58左子树高度为2，而右子树为高度为0，BF>1
• ④是AVL树

最小不平衡子树：距离插入点最近的，且平衡因子绝对值大于1的结点为根的子树

如下，当插入新节点37时，距离它最近的平衡因子绝对值超过1的结点是58，所以58开始以下的子树为最小不平衡子树

二：AVL树实现原理

（1）构建AVL树

AVL树构建思想：在构建二叉排序树的过程中，每当插入一个结点时，先检查该结点的插入是否导致了平衡性被破坏，若不是则继续插入；若是则找出最小不平衡子树，在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点的链接关系，也即平衡调整，进行相应的旋转，使之成为新的平衡子树

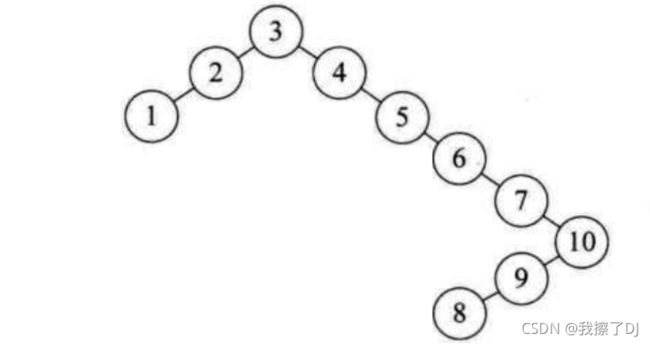
int arr[10]={3,2,1,4,5,6,7,10,9,8}

假设上面数组需要构建为AVL树，由于AVL树首先是BST树，所以会构建成下面这样

但是我们知道，BST树很忌讳其高度太高，所以如果能调整为下面这样那再合适不过了，因为下面的树依然是一棵BST树，但是其高度小了很多，查找效率自然也会得到提高

因此对于AVL树的研究重点就在于如何调整，也就是如何旋转

（2）构建演示

对于$3$和$2$，构建时没有任何问题

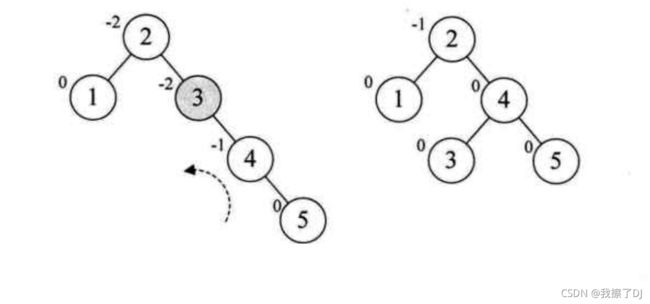
来到$1$并将其插入后，发现根节点$3$的平衡因子变为了2，此时整棵树成为最小不平衡子树，需要进行调整：右单旋转调整(点击跳转查看)

• 因为此时结点插入到了较高左树左侧

• 调整后，$2$成为了根节点，$3$成为了$2$的右孩子，此树高度平衡

接着结点$4$到来，平衡因子没有变化

接着结点$5$到来，结点$3$的平衡因子变为-2，需要进行调整：左单旋转调整(点击跳转查看)

• 因为此时结点插入到了较高右树右侧
  

• 再次达到平衡

接着结点$6$到来，此时根节点$2$的平衡因子变为了-2，进行调整 左单旋转调整(点击跳转查看)

• 因为此时结点插入到了较高右树右侧

结点$7$到来，结点5的平衡因子变为了-2，进行调整 左单旋转调整(点击跳转查看)

• 因为此时结点插入到了较高右树右侧

结点$10$到来，结构无变化

结点$9$到来，此时结点$7$的BF变为了-2，理应进行左单旋转调整，但是由于此时新结点插入到了较高右树左侧，故直接使用左单旋转调整是不可以的。（具体原因跳转过去会详细解释），需要进行 先右后左双旋转调整(点击跳转查看)

• 很明显$9$插入了$7$的右子树左侧，故不能直接使用左单旋转

• 故先对$9$和$10$进行右旋，再对$7$、$9$和$10$进行左旋

接着结点$8$插入，使结点$6$的BF变为了-2，属于插入到了较高右树的左侧，故需要进行 先右后左双旋转调整(点击跳转查看)

（3）旋转方法

大家最头疼的可能就是如何选择旋转方法了，总结如下，只需按照如下逻辑选择即可

A：右单旋转调整（插入到较高左子树左侧）

下图中为抽象树，三角形表示的树为高度平衡的二叉树排序树。如下情况中，结点A的平衡因子绝对值为1，左子树较高

此时来了一个新的结点恰好插入到了B结点的左树，导致A结点的平衡因子变为2，树不平衡，需要进行调整

调整时：将结点A下移一个高度，B上移一个高度，然后把B的右子树挂在A的左子树处（这样做可以保证二叉排序树的特性）

B：左单旋转调整（插入到较高右子树右侧）

左单调整和右单调整情况恰好相反，调整时结点B上移，结点A下移，让结点B的左子树做结点A的右子树

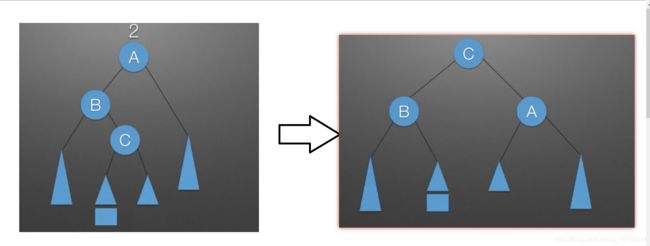
C：先左后右双旋转调整（插入到较高左子树右侧）

在右单旋转调整中，由于新的结点插入到了较高左子树的左侧，所以调整后可以使树平衡

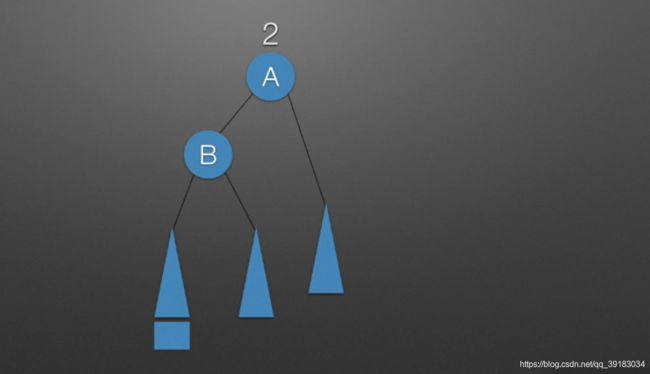
但如果此时将新结点插入到较高左子树的右侧

此时如果继续使用右单旋转调整，你会发现怎么也调整不过去，依然不平衡

在这种情况下就要使用到双旋转调整了

我们先把较高左子树的右子树拆分一下，拆分为两棵树

大家会发现此时如果要在B的右侧插入一个结点有两个选择——要么插入到C的左侧，要么插入到C的右侧
这里我以插入到C的右侧为例

接着进行双旋转调整：先对B树进行左单旋转

形成了这样一颗树

然后对这颗树再进行右单旋转调整，树就平衡了

• 本例是插入到了C的右侧，如果插入到了C的左侧，调整也是一样的
  

D：先右后左双旋转调整（插入到较高右子树左侧）

• 特别注意：先看C部分再看本部分，C部分中解释较为详细，本部分只是逻辑相反

在左单旋转调整中，面对的情况是新节点插入到了较高右子树的右侧，而如果新节点插入到了较高右子树的左侧，那么就要使用先右后左双旋转调整

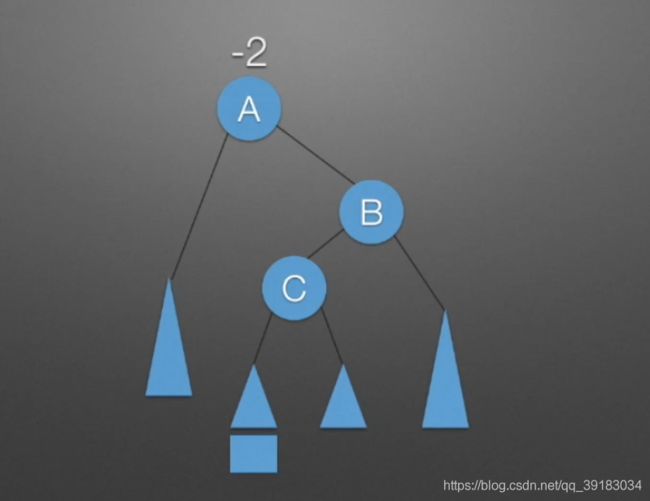
所以在这种情况下，先对右子树进行右单旋转调整，然后再进行左单旋转调整

三：AVL树相关代码

对于AVL树考研数据结构基本不涉及代码，其旋转过程逻辑并不难，只是需要多捋一捋。其代码实现有很多值得注意的地方，且稍不留心就容易掉坑，有兴趣的同学可以查看我的另一篇文章，其中代码都是可以跑通的，用C++实现

点击跳转