【Java数据结构】栈和队列

一、 栈(Stack)

1、概念

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据在栈顶。

栈的特点是 先进后出

Java虚拟机栈：JVM stack 是JVM中的一块内存，调用函数的时候，在JVM stack 开辟一块内存，叫做栈帧

2、入栈和出栈的顺序

一个栈的入栈序列是a b c d e，栈不可能出栈序列为（）：
A. edcba
B.decba
C.dceab
D.abcde

一个栈的入栈序列是m n x y z，栈不可能出栈序列为（）：
A. mnxyz
B. xnyzm
C. nymxz
D. nmyzx

了解了栈的概念，解决以上问题

解释：1. 入栈a b c d 此时d c出栈，e没有，入栈再出栈，下一个a要出栈，先要出b，顺序应该是ba，所以答案C错误
2. 同样，答案C中，第一个出n，所以m压栈，n压栈再出栈，接着x压栈，y压栈再出栈，下一个要出m先得出x

3、中缀表达式转后缀表达式

例如：求 (5 + 4) * 3 - 2的后缀表达式
做法：先按照运算顺序加括号，再将所有运算符放到括号后，最后去除我们加上的括号
(((5 + 4) * 3) - 2)
(((5 4)+ 3)* 2)-
5 4+ 3 * 2 -

如果通过这个后缀表达式求值？
用 i 遍历这个表达式，数字压栈，遇到运算符，弹出栈顶的两个元素，第一个放在运算符右边，否则减法就会错顺序

---

4、栈的方法

public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>();
        // 压栈
        stack.push(11);
        stack.push(22);
        stack.push(33);
        // 弹出栈顶元素，并删除
        System.out.println(stack.pop()); // 33
        // 获取栈顶元素，但不删除
        System.out.println(stack.peek()); // 22
        // 是否为空
        System.out.println(stack.empty()); // false
        // 查找
        System.out.println(stack.search(22)); // 1

		Deque<Integer> stack1 = new ArrayDeque<Integer>();
    }

继承的方法等：

LeetCode 150. 逆波兰表达式求值

150. 逆波兰表达式求值

根据 逆波兰表示法，求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：
输入：tokens = [“2”,“1”,“+”,“3”,“*”]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
        for(int i = 0; i < tokens.length; i++) {
            String val = tokens[i];
            if(!isOperation(val)) {
                // 不是运算符
                stack.push(Integer.parseInt(val)); // 转为数字
            } else {
                // 是运算符 计算
                int num1 = stack.pop();
                int num2 = stack.pop();
                switch(val) {
                    case "+":
                      stack.push(num2 + num1);
                      break;
                    case "-":
                        stack.push(num2 - num1);
                        break;
                    case "*":
                        stack.push(num2 * num1);
                        break;
                    case "/":
                        stack.push(num2 / num1);
                        break;
                }
            }
        }
        return stack.pop();
    }

    private boolean isOperation(String x) {
        if(x.equals("+") || x.equals("-") || x.equals("*") || x.equals("/")) {
            return true;
        }
        return false;
    }
}

剑指 Offer 31. 栈的压入、弹出序列

剑指 Offer 31. 栈的压入、弹出序列

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

示例 1：
输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        Stack<Integer> stack = new Stack<>();
        int j = 0;
        for(int i = 0; i < pushed.length; i++) {
            stack.push(pushed[i]); // 遍历pushA数组 放入栈中
            // 循环判断 栈顶元素和当前 j 下标是否一样 一样就弹出
            while(!stack.empty() && j < popped.length && stack.peek() == popped[j]) {
                stack.pop();
                j++;
            }
        }
        return stack.empty();
    }
}

5、栈的实现

public class MyStack {
    public int[] elem;
    public int usedSize;

    public MyStack() {
        this.elem = new int[5];
    }

    public void push(int val) {
        if(isFull()) { // 2被扩容
            this.elem = Arrays.copyOf(this.elem, 2*this.elem.length);
        }
        this.elem[this.usedSize] = val;
        this.usedSize++;
    }

    // 判断数组满
    public boolean isFull() {
        return this.usedSize == this.elem.length;
    }

    public int pop() {
        if(isEmpty()) {
            throw new RuntimeException("栈为空");
        }
        int oldVal = this.elem[usedSize - 1];
        this.usedSize--;
        return oldVal;
    }

    public int peek() {
        if(isEmpty()) {
            throw new RuntimeException("栈为空");
        }
        return this.elem[usedSize - 1];
    }

    // 判断空
    public boolean isEmpty() {
        return this.usedSize == 0;
    }
}

LeetCode 20. 有效的括号

20. 有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例 1：
输入：s = “()”
输出：true

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for(int i = 0; i < s.length(); i++) {
            char ch = s.charAt(i);
            if(ch == '(' || ch == '{' || ch == '[') {
                // 左括号 入栈
                stack.push(ch);
            } else {
                // 右括号 匹配
                if(stack.empty()) {
                    return false; // 右括号多
                }
                char top = stack.peek(); // 栈顶元素
                if(top == '(' && ch == ')' || top == '[' && ch == ']' || top == '{' && ch == '}') {
                    stack.pop();
                } else {
                    return false; // 左右括号不匹配
                }
            }
        }
        return stack.empty(); // 不为空 左括号多
    }
}

LeetCode 155. 最小栈

155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。

示例:
输入：
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

class MinStack {
    // private Stack stack = new Stack<>();
    // private Stack minStack = new Stack<>();
    Stack<Integer> stack;
    Stack<Integer> minStack;

    public MinStack() {
         stack = new Stack<>();
         minStack = new Stack<>();
    }
    
    public void push(int val) {
        stack.push(val);
        if(!minStack.empty()) { // 不为空
            int top = minStack.peek(); // 判断minStack是否要加入
            if(val <= top) { // 小于等于 也要放进去
                minStack.push(val);
            }
        } else {
            minStack.push(val);
        }
    }
    
    public void pop() {
        int popVal = stack.pop();
        if(!minStack.empty()) {
            int top = minStack.peek();
            if(top == popVal) { // 判断minStack是否要删除
                minStack.pop();
            }
        }
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return minStack.peek();
    }
}

---

二、队列

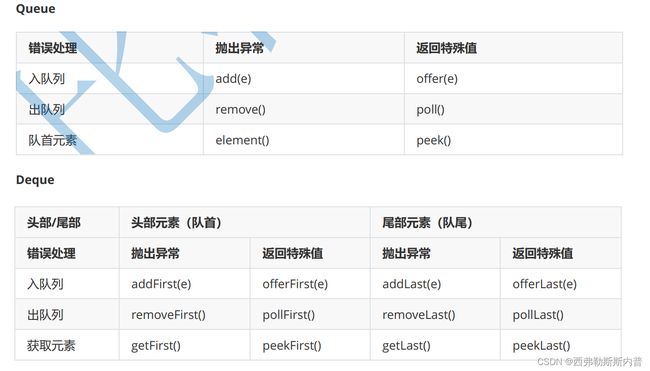
1、普通队列 与 双端队列

队列：（queue）只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾（Tail/Rear） 出队列：进行删除操作的一端称为队头
（Head/Front）

双端队列：（deque）是指允许两端都可以进行入队和出队操作的队列，deque 是 “double ended queue” 的简称。
那就说明元素可以从队头出队和入队，也可以从队尾出队和入队。

import java.util.Deque;
import java.util.LinkedList;
import java.util.Queue;

public class TestDemo {
    public static void main(String[] args) {
        Queue<Integer> queue = new LinkedList<>();
        // 入队列
        queue.add(1); // 容量限制 -> 可能对抛异常
        queue.offer(2);
        // 获取队首元素
        System.out.println(queue.peek()); // 1
        System.out.println(queue.element()); // 1
        // 出队列
        System.out.println(queue.poll()); // 1
        System.out.println(queue.remove()); // 2

        System.out.println("================");

        Deque<Integer> queue2 = new LinkedList<>();
        queue2.offerFirst(1);
        queue2.offerFirst(2);
        queue2.offer(3); // 默认队尾入队
        // 2 1 3
        System.out.println(queue2.peek()); // 2 默认获取队首元素
        System.out.println(queue2.peekFirst()); // 2
        System.out.println(queue2.peekLast()); // 3
    }
}

2、单链表实现队列

对LinkedList来说，不仅可以当做普通的队列，也可以当做双端队列，也可以当做双向链表，也可以当做栈。

用单链表来实现队列，用一个last 指针实现时间复杂度O(1)

class Node {
    public int val;
    public Node next;
    public Node(int val) {
        this.val = val;
    }
}

public class MyQueue {
    public Node head;
    public Node last;

    /**
     * 尾插
     * @param val
     */
    public void offer(int val) {
        Node node = new Node(val);
        if(this.head == null) {
            this.head = node;
            last = node;
        } else {
            last.next = node;
            last = last.next;
        }
    }

    /**
     * 出队列
     * @return
     */
    public int poll() {
        if(isEmpty()) {
            throw new RuntimeException("队列为空");
        }
        int oldVal = head.val;
        this.head = head.next;
        return oldVal;
    }

    public boolean isEmpty() {
        return this.head == null;
    }

    public int peek() {
        if(isEmpty()) {
            throw new RuntimeException("队列为空");
        }
        return head.val;
    }
}

// 测试：
public static void main(String[] args) {
        MyQueue queue = new MyQueue();
        queue.offer(1);
        queue.offer(2);
        queue.offer(3);
        System.out.println(queue.poll()); // 1
        System.out.println(queue.poll()); // 2
        System.out.println(queue.poll()); // 3
}

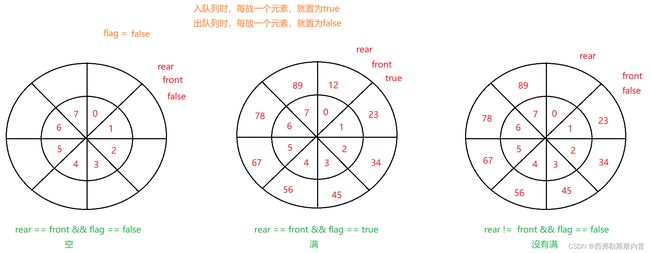
3、 循环队列

如何区分空与满：

• 第一种解决方式：使用usedSize.使用usedSize和数组长度比较，确定满或者空。

• 第二种解决方式：使用标志位

• 第三种解决方式：保留一个位置 front == rear
  每次存放元素之前，都先检查一下rear的下一个是不是front。如果是那么就是满的。

LeetCode 622. 设计循环队列

622. 设计循环队列

你的实现应该支持如下操作：

MyCircularQueue(k): 构造器，设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。

class MyCircularQueue {

    public int[] elem;
    public int front; // 对头下标
    public int rear; // 队尾下标

    public MyCircularQueue(int k) {
        this.elem = new int[k + 1]; // k + 1
    }

    // 入队列
    public boolean enQueue(int value) {
        if(isFull()) return false;
        this.elem[rear] = value;
        rear = (rear + 1) % elem.length;
        return true;
    }

    // 出队列
    public boolean deQueue() {
        if(isEmpty()) return false;
        front = (front +  1) % elem.length;
        return true;
    }

    // 得到队头元素
    public int Front() {
        if(isEmpty()) return -1;
        return elem[front];
    }

    // 得到队尾元素
    public int Rear() {
        if(isEmpty()) return -1;
        int index = -1;
        if(rear == 0) {
            index = elem.length - 1;
        } else {
            index = rear - 1;
        }
        return elem[index];
    }

    public boolean isEmpty() {
        return front == rear; // 相遇
    }

    public boolean isFull() {
        // rear 的下一个是 front
        if((this.rear + 1) % elem.length == front) {
            return true;
        }
        return false;
    }
}

LeetCode 225. 用队列实现栈

225. 用队列实现栈

// 入栈时，入到不为空的队列，都为空就指定一个
// 出栈时，在不为空的队列，出 size - 1 个元素，剩下的一个就是要出栈的元素
public class MyStack {

    public Queue<Integer> qu1;
    public Queue<Integer> qu2;

    public MyStack() {
        qu1 = new LinkedList<>();
        qu2 = new LinkedList<>();
    }

    public void push(int x) {
        if(!qu1.isEmpty()) {
            qu1.offer(x);
        } else if (!qu2.isEmpty()) {
            qu2.offer(x);
        } else {
            qu1.offer(x); // 都为空 指定一个
        }
    }

    public int pop() {
        if(empty()) return -1;

        if(!qu1.isEmpty()) {
            int size = qu1.size();
            for (int i = 0; i < size - 1; i++) {
                int val = qu1.poll();
                qu2.offer(val);
            }
            return qu1.poll();
        }
        if(!qu2.isEmpty()) {
            int size = qu2.size();
            for (int i = 0; i < size - 1; i++) {
                int val = qu2.poll();
                qu1.offer(val);
            }
            return qu2.poll();
        }

        return -1;
    }

    public int top() {
        if(empty()) return -1;

        if(!qu1.isEmpty()) {
            int val = -1;
            int size = qu1.size();
            for (int i = 0; i < size; i++) {
                val = qu1.poll();
                qu2.offer(val);
            }
            return val;
        }
        if(!qu2.isEmpty()) {
            int val = -1;
            int size = qu2.size();
            for (int i = 0; i < size; i++) {
                val = qu2.poll();
                qu1.offer(val);
            }
            return val;
        }

        return -1;
    }

    public boolean empty() {
        return qu1.isEmpty() && qu2.isEmpty();
    }
}

LeetCode 232. 用栈实现队列

添加链接描述

class MyQueue {
    // 入队的时候，统一入到第1 个栈
    // 出队的时候，统一出第2 个栈的元素，如果第二个栈为空，将第1 个栈的所有元素导入，再出栈顶元素，相当于倒了个顺序
    public Stack<Integer> stack1;
    public Stack<Integer> stack2;

    public MyQueue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }
    
    public void push(int x) {
        stack1.push(x);
    }
    
    public int pop() {
        if(empty()) return -1;

        if(stack2.empty()) {
            while(!stack1.empty()) {
                // int val = stack1.pop();
                // stack2.push(val);
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
    
    public int peek() {
        if(empty()) return -1;
        if(stack2.empty()) {
            while(!stack1.empty()) {
                stack2.push(stack1.pop());
            }
        }
        return stack2.peek();
    }
    
    public boolean empty() {
        return stack1.empty() && stack2.empty();
    }
}