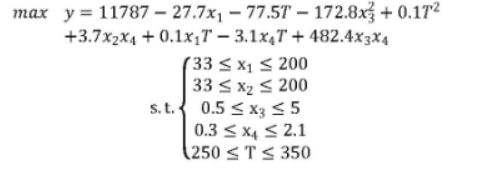2021数学建模国赛B题复盘详细解析

声明：本赛题为去年的题目，想着2022的国赛即将来临，我决定花一个晚上再次回顾经典题目。
未经允许，不得转载。——CSDN:川川菜鸟

题目

C4 烯烃广泛应用于化工产品及医药的生产，乙醇是生产制备 C4 烯烃的原料。在制备过程中，催化剂组合（即：Co 负载量、Co/SiO2 和 HAP 装料比、乙醇浓度的组合）与温度对 C4 烯烃的选择性和 C4 烯烃收率将产生影响（名词解释见附录）。因此通过对催化剂组合设计，探索乙醇催化偶合制备 C4 烯烃的工艺条件具有非常重要的意义和价值。
某化工实验室针对不同催化剂在不同温度下做了一系列实验，结果如附件 1 和附件 2 所示。请通过数学建模完成下列问题

问题

第一问
对附件 1 中每种催化剂组合，分别研究乙醇转化率、C4 烯烃的选择性与温度的关系，并对附件 2 中 350 度时给定的催化剂组合在一次实验不同时间的测试结果进行分析。

第二问
探讨不同催化剂组合及温度对乙醇转化率以及 C4 烯烃选择性大小的影响

第三问
如何选择催化剂组合与温度，使得在相同实验条件下 C4 烯烃收率尽可能高。若使温度低于 350 度，又如何选择催化剂组合与温度，使得 C4 烯烃收率尽可能高。

第四问
如果允许再增加 5 次实验，应如何设计，并给出详细理由。

名词解释与附件说明

第一问

分析

题目首先看前面部分，关键词：”附件1“，”每种“，”分别研究“，”关系“，“附件2”，“350度”

先看前面部分的附件1：

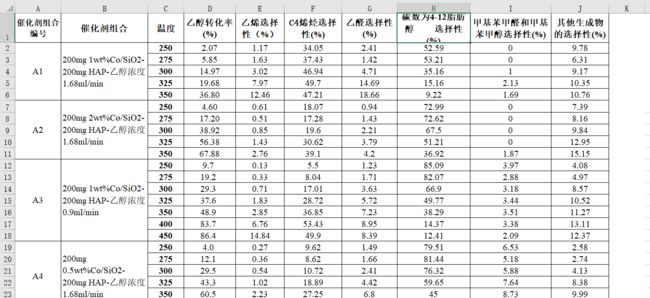
重新读题：“每种组合”，对应附件1数据中的第二列，先大概看看即可，主要是对应数据。

继续看第二句话：“分别研究…和温度的关系”。那么先只研究乙醇转化率和温度的关系，因此需要控制其它的变量是不变化的，这是很简单的控制变量法思想。我们希望乙醇转化率是x,温度是y,最后有可能类似y=ax+b的关系，如果其它变量发生变化，那就成了x1,x2…了，所以控制变量法。

为此，认真看数据第二列，数据比较多，需要理解一下，以A1的催化剂组合为例：

200mg 1wt%Co/SiO2- 200mg HAP-乙醇浓度1.68ml/min

它的含义是：Co/SiO2 和 HAP 质量比为 200mg：200mg，且乙醇按每分钟 1.68 毫升加入。其中Co 与 SiO2 的重量之比为1:100(即1wt%)。

关于多项式的基础，其实本博客已经写过，照猫画虎：

第一小问

经过上述分析，回归问题。对于每种催化剂组合，分别建立温度与乙醇转化率、温度与 C4 烯烃选择性的关系模型。

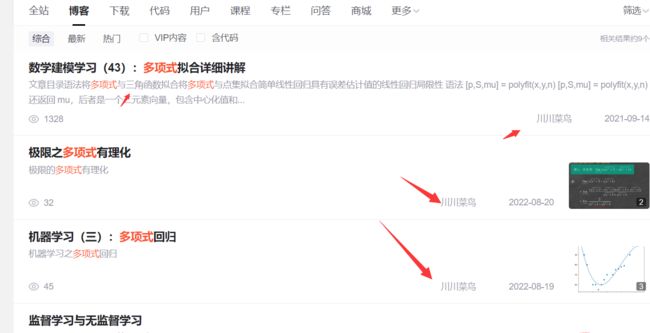
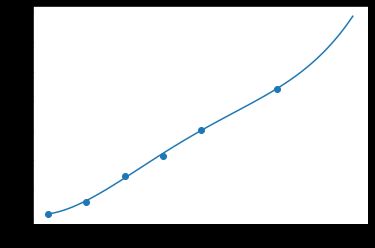
以A1组为例,先绘制出散点图，大概看看什么关系：

import numpy as np
import matplotlib.pyplot as plt

x=np.array([250,275,300,325,350]).reshape((-1, 1))
y=np.array([2.07,5.85,14.97,19.68,36.80])

plt.scatter(x, y) # 绘制散点图
plt.show()

如下：

一眼看过去，线性勉强，至少我可以一眼看出它还可以用一个曲线表示，因此我觉得不用线性模型，而是非线性。

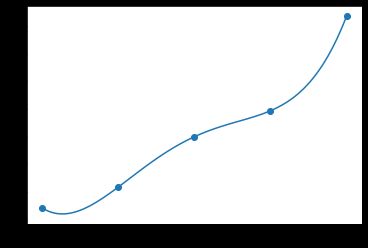
如果用线性模型拟合：

from sklearn.linear_model import LinearRegression
#实例化线性模型
lr = LinearRegression()
lr.fit(x, y)
y_predict = lr.predict(x)

plt.scatter(x, y )
plt.plot(x, y_predict)

如下，明显误差很大：

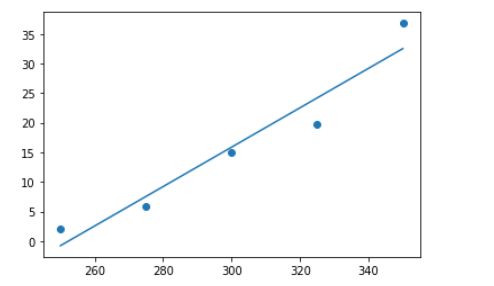
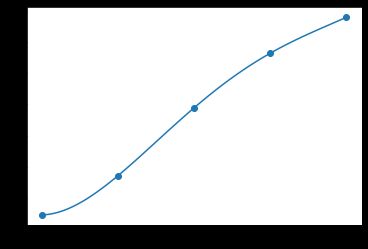
所以我采用多项式的方法进行拟合以A1为例：

import numpy 
x=[250,275,300,325,350]
y=[2.07,5.85,14.97,19.68,36.80]


mymodel = numpy.poly1d(numpy.polyfit(x, y, 4)) # 三阶

myline = numpy.linspace(250, 350, 100) #

plt.scatter(x, y) # 原始点 
plt.plot(myline, mymodel(myline)) # 多项式回归
plt.show() #显示

拟合如下：

同理 A2:

A3拟合：

A4拟合：

后续同样类似操作，可见是肯定能百分百拟合的！

下一个问题：得到数学模型，也就是数学公式。这里以A4为例，其它操作方法相同，只需要添加一行代码即可：

print(numpy.polyfit(x4, y4, 4))

结果如下：

[ 2.36276730e-07 -3.22254088e-04 1.63402013e-01 -3.58919245e+01
2.87645755e+03]

则公式(数学模型）为：y=2.36276730e-07 * x ^4 -3.22254088e-04 * x^3 + 1.63402013e-01 * x ^2 -3.58919245e+01 * x + 2.87645755e+03

其它每一组用同样方法求出来方程，这是必须的！因为题目有说到得到关系。

既然说到关系，还可以看看相关性，这里以A4为例：

import pandas as pd

x4=[250,275,300,325,350,400]
y4=[4.0,12.1,29.5,43.3,60.5,88.4]

data = [[250,4],[275,12.1],[300,29.5],[325,43.3],[350,60.5],[400,88.4]]

df = pd.DataFrame(data,columns=['x1','x2']) # 将第一维度数据转为为行，第二维度数据转化为列，即 3 行 2 列，并设置列标签

c1=df['x1']
c2=df['x2']

result= np.corrcoef(c1,c2)
result

如下，可见完全相关：

array([[1.        , 0.99751423],
       [0.99751423, 1.        ]])

热力图：

import matplotlib.pyplot as plt
figure, ax = plt.subplots(figsize=(12, 12))
sns.heatmap(df.corr(), square=True, annot=True, ax=ax)

如下在此证明十分相关：

还可以得出一个结论：在相同的催化剂组合条件下，温度越高，反应的活化分子数越多，有效碰撞增加，因此可以加快化学反应，乙醇的转化率越高。

第二小问

这个问题是：C4 烯烃的选择性与温度的关系

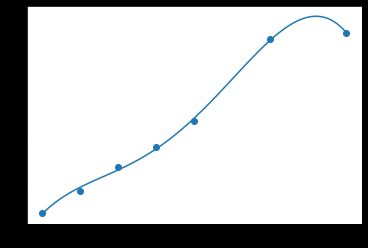
方法依然使用第一小问中的方法，进行多项式拟合，以A1为例，经过调试四阶依然刚好达到最好效果：

x=[250,275,300,325,350]
z=[34.05,37.43,46.94,49.7,47.21]

model = numpy.poly1d(numpy.polyfit(x, z, 4)) # 4阶

line = numpy.linspace(250, 350, 1000) 

plt.scatter(x, z) # 原始点 
plt.plot(line, model (line)) # 多项式回归
plt.show() #显示

如下：

同理获得其它组的最佳拟合图以及拟合后数学方程。

第三小问

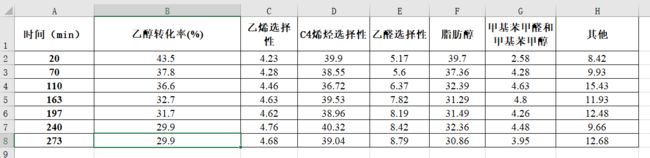
对附件 2 中 350 度时给定的催化剂组合在一次实验不同时间的测试结果进行分析。

打开数据看看：

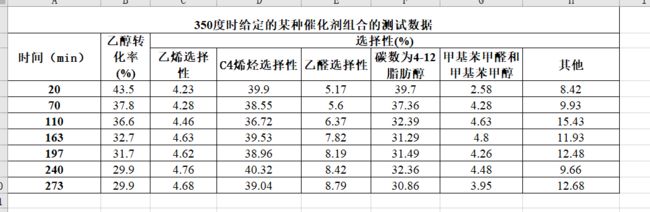
先不管那么那么多绘制图形看看规律，时间为x轴，乙醇转化率为左侧轴，选择性为右侧轴。也就是可视化中的双Y轴图像。在excel中也叫做二维折线图 。

数据稍微修改一下更加整洁：

编写绘制双y轴代码：

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文

fig = plt.figure(figsize=(7, 4),dpi=150)  # 大小和清晰度
ax1 = fig.add_subplot(111)

ax1.plot(x, y1)
ax1.set_ylabel('乙醇转化率')
ax1.set_title("350℃下乙醇转化率和各种生成物的选择性随时间变化曲线")

ax2 = ax1.twinx()  

ax2.plot(x, y2)
ax2.plot(x, y3)
ax2.plot(x, y4)
ax2.plot(x, y5)
ax2.plot(x, y6)


ax2.set_ylabel('选择性')

plt.legend(data.columns,fontsize = 10) # 图标
plt.savefig(r"双y轴.png")
plt.show()

绘制结果如下：

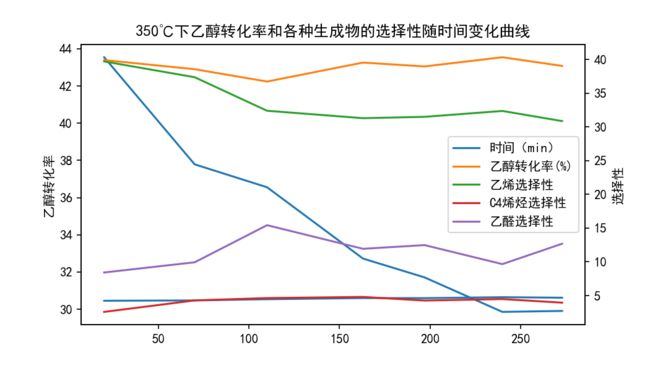
随着反应的进行，乙醇转化率降低，也即乙醇的反应速率在下降，原因是乙醇的浓度在降低。在这个过程中，乙醇不断脱氢生成乙醛，乙醛的生成速率大于其消耗速率，因此乙醛在生成物中的占比不断增加，其选择性增加。由于 C4 烯烃制备过程的最后一步通常是由脂肪醇脱水生成，因此反应进行到 200 分钟时，脂肪醇和 C4 烯烃的选择性的变化趋势基本相同。当反应进行 240 分钟后，乙醇转化率不再随时间发生变化，也即乙醇的反应速率保持不变，因此可认为反应在 240 分钟时达到平衡态。

拓展思路

可以使用Matlab中的 Curve Fitting工具箱的polyfit()函数对该模型进行求解拟合，从而得到回归方程。

第二问

探讨不同催化剂组合及温度 对 乙醇转化率以及 C4 烯烃选择性大小的影响。

分析

关键词：”影响“。再次看看附件1数据，对照题目要求。

既然说到一个东西对另外一个东西的影响，这里明显就是双因素方差分析 。双因素分别为温度和不同催化剂组合，通过判断这两个因素对乙醇转化率以及 C4 烯烃选择性大小两者的显著性来获得结果。如果你看过我 数学建模专栏 和机器学习专栏，我相信本篇文章所有解析都能轻松理解。除了双因素方差分析意外，其实机器学习中的岭回归也可以得到影响的一个好还是坏。

再详细一点：
自变量：即催化剂组合以及温度两个自变量。
因变量：即乙醇转化率以及 C4 烯烃选择性两个因变量。
既然谈
其中：每一个催化剂组合都是4个自变量：Co/Si02的质量、HAP质量、Co负载量、每分钟加入乙醇量。

综上，这题就是一个 5 个自变量，2 个因变量

做完双因素方差分析后，还需要做 多重比较，通过该方法可以得到更具体结果。

拓展

除了使用方差方法以外，也可以通过某种方法得到变量的重要性排序 。自然想到是回归这个大类，其中最常见的方法我认为可以是随机森林，神经网络 ，多元回归。 通过以上地某种方法可以得到各个变量地权重，从而得到影响力大小。

比如随机森林得到地结果：

重要性排名：

第三问

第一小问：如何选择催化剂组合与温度，使得在相同实验条件下 C4 烯烃收率尽可能高。（注意：C4 烯烃收率：其值为乙醇转化率  C4 烯烃的选择性）
第二小问：若使温度低于 350 度，又如何选择催化剂组合与温度，使得 C4 烯烃收率尽可能高。

分析

关键词：”尽可能高“，那就是最优问题。

令 C4 烯烃收率为因变量。通过第二问分析可知有五个自变量，这里将催化剂中四个组成因素与温度作为5个自变量，建立多元非线性模型，即五元二次方程。

设Co/Si02的质量、HAP质量、Co负载量、每分钟加入乙醇量分别为x1,x2,x3,x4。温度T为第五个自变量。

根据公式：C4 烯烃收率=乙醇转化率 * C4 烯烃的选择性。

装料方式一 情况下拟合出五元二次方程。参考结果如下：

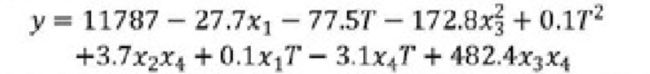
装料方式二情况下，同样的进行拟合，得到三元二次方程结果如下：

y =10238-33.5x1一64.7T＋0.1T^2+0.1x1*T-0.7x4*T

方式一建立模型如下：

方式二建立模型 如下：

得到模型后，就是求最大值问题了，使用遗传算法求解即可,这是很容易的事，不再过多强调。

拓展

除了上述方法以外，还可以使用BP神经网络来做，可以理解为多输入单输出的BP，如下：

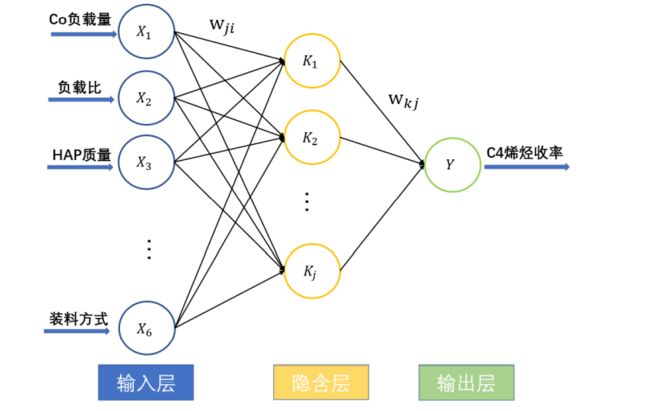
当然除了多元非线性还可以多元线性，同样的方式拟合也是可以的。

乙醇转化率的多元线性方程最终拟合得到结果如下：

1 = −70.3901 − 16.22331 − 4.06392 + 0.09793 + 0.33394 − 8.46025
− 6.22756

C4 烯烃选择性为：

2 = −30.845 − 3491 − 11.84552 + 0.07533 + 0.18194 + 3.11665
− 3.49896

而我们的目标是：

 = 1 · 2 

第四问

如果允许再增加 5 次实验，应如何设计，并给出详细理由。

分析

这个就比较开放，当时也不是乱做，需要基于第三问的最优模型，以及第二问。

比如增加一个实验：根据问题二的方差分析原理，建立方差分析模型，探究不同催化剂组合与温度对烯经收率的影响。温度越高，烯经收率越高，在400℃时达到温度最优;催化剂组合影响力大小排序。

比如增加一个实验：使用岭回归算法对催化剂组合与温度条件进行一次实验。

往年赛题思路回顾

去年写的这个赛题思路，当时我是第一次参加比赛，没注意到比赛的重要性，也把自己做题的思路发出来了：2021 全国大学生数学建模完整B 题思路分析。由于时间的紧迫性，当时是写很粗糙的，经过一年的成长我再次写下思路，以做对比。

需要赛前辅导请点击查看：数学建模