c++画分形之Julia集与Mandelbrot集
Julia集是一个在复平面上形成分形的点的集合,它最早由法国数学家Gaston Julia发现。
Julia集合可以由下式进行反复迭代得到:f(z) = z2 + c, 其中z是复平面某一点,c是一个复常数。把这个公式反复迭代,最终会得到一个复数C,然后根据C的模的大小,把这个点映射成不同的颜色,漂亮的Julia集分形就出来了。可以参阅M67的这篇文章,其中有详细的介绍。
下面的几幅图是我用c++和opencv画出来的,一张500*500的图片,迭代15次,在我的i5电脑上跑约不到10秒,速度稍慢。图中不同的C值对应着不同的Julia集,配色比较烂,大家凑合着看。
c = 0.73i
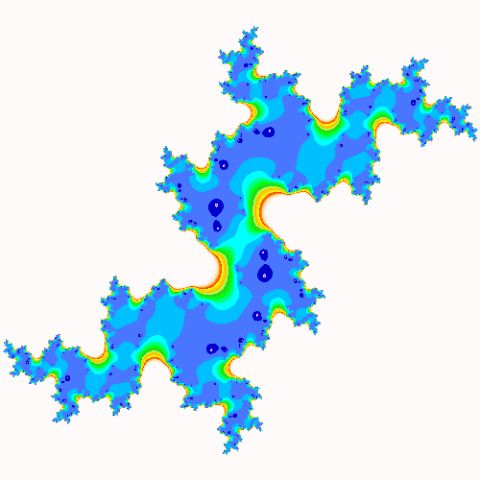
c = -0.3128 + 0.756i
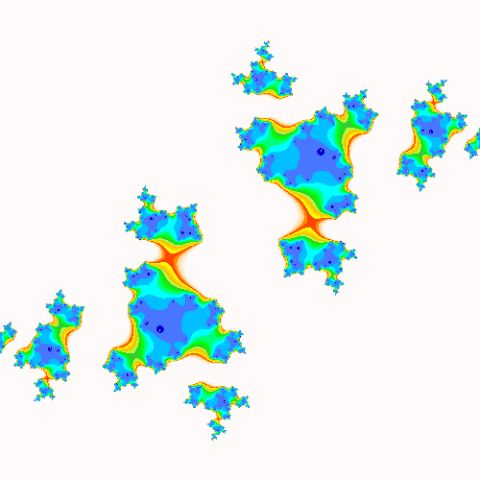
c = 0.45
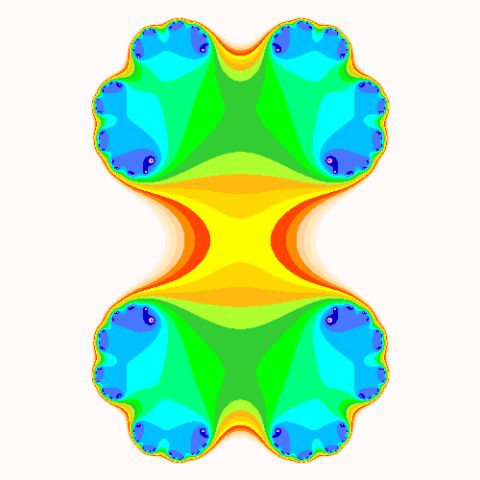
c = 0.3
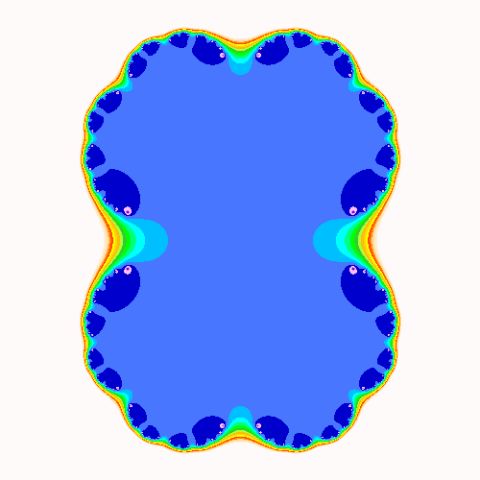
当把复数C替换成该点的坐标时,著名的Mandelbrot集就出现了,图中每一个像素点都是一个Julia集。可以把Mandlbrot集是理解为是Julia集的一个缩影,图中不同的颜色表示该点所在的Julia集的发散速度。这张我图画的很不满意,因为迭代次数太少,精度不够,而且颜色也非常难看。在我的x86系统上迭代15次就已经有一些点会overflow了,叹气!期待高人指点

这里盗用M67的一段话:“生成 Mandelbrot 集的算法和生成 Julia 集的算法完全一样,只是这一次我们固定的是初始值,而把 c 当作了变量。Mandelbrot 集内的每一个点就对应了一个连通的 Julia 集,Mandelbrot 集合外的点则对应了不连通的 Julia 集,并且很容易想到,越靠近 Mandelbrot 集的边界,对应的 Julia 集形状就越诡异。因此, Mandelbrot 集还有另外一种解读方法:它就是 Julia 集的缩略图!完全没有比喻的意思,它真的就是 Julia 集的缩略图”。此处的初始值就是每个像素点所在坐标。

代码如下,c和d对应着上文中复数C的实部和虚部,改变它们就可以生成不同的Julia集
其中有两行注释掉的语句,把它们和上两行替换掉,程序就可以画出Mandelbrot集了。颜色的配置我写的很麻烦,因为自己手工设置的有一种亲切感。
#include "stdafx.h" #include <cv.h> #include <highgui.h> #include <cxcore.h> const int icount = 15; //迭代次数 const float c = -0.3128; //实部 const float d = 0.756; //虚部
double m_real, m_image; //Mandelbro集
CvScalar colortab[21]; class Complex { public: double real; double image; Complex(double r=0, double i=0){real = r, image = i;} }; Complex operator+(const Complex& a, const Complex &b) { Complex c; c.real = a.real + b.real; c.image = a.image + b.image; return c; } Complex operator*(const Complex& a, const Complex &b) { Complex c; c.real = a.real * b.real - a.image * b.image; c.image = a.image * b.real + a.real * b.image; return c; } double Model(Complex a) { return sqrtf(a.real * a.real + a.image * a.image); } double Iteration(Complex a, int n) { if(n==0) return Model(a); else { Complex temp = a*a ; temp.real += c; temp.image += d;
// temp.real += m_real; 把这两句代替前面的两句就是mandelbrot集了
// temp.image += m_image;
return Iteration(temp, n-1);
}
} CvScalar dye(double dist) { if(dist < 1.0/4096) return colortab[0]; else if(dist < 1.0/1024) return colortab[1]; else if(dist < 1.0/256) return colortab[2]; else if(dist < 1.0/64) return colortab[3]; else if(dist < 1.0/16) return colortab[4]; else if(dist < 1.0/4) return colortab[5]; else if(dist < 1) return colortab[6]; else if(dist < 4) return colortab[7]; else if(dist < 16) return colortab[8]; else if(dist < 64) return colortab[9]; else if(dist < 256) return colortab[10]; else if(dist < 1024) return colortab[11]; else if(dist < 4096) return colortab[12]; else if(dist < 16384) return colortab[13]; else if(dist < 65536) return colortab[14]; else if(dist < 262144) return colortab[15]; else if(dist < 1048576) return colortab[16]; else if(dist < 4194304) return colortab[17]; else if(dist < 16777216) return colortab[18]; else if(dist < 67108864) return colortab[19]; else return colortab[20]; } int _tmain(int argc, _TCHAR* argv[]) { colortab[0] = CV_RGB(28, 28, 28); colortab[1] = CV_RGB(130, 130, 130); colortab[2] = CV_RGB(85, 26, 139); colortab[3] = CV_RGB(224, 102, 255); colortab[4] = CV_RGB(255, 187, 255); colortab[5] = CV_RGB(0,0,205); colortab[6] = CV_RGB(72, 118, 255); colortab[7] = CV_RGB(0, 191, 255); colortab[8] = CV_RGB(0, 255, 255); colortab[9] = CV_RGB(0, 255, 127); colortab[10] = CV_RGB(0, 255, 0); colortab[11] = CV_RGB(50, 205, 50); colortab[12] = CV_RGB(173, 255, 47); colortab[13] = CV_RGB(255, 185, 15); colortab[14] = CV_RGB(255, 215, 0); colortab[15] = CV_RGB(255, 255, 0); colortab[16] = CV_RGB(255, 69, 0); colortab[17] = CV_RGB(255, 140, 0); colortab[18] = CV_RGB(255, 211, 155); colortab[19] = CV_RGB(255, 231, 186); colortab[20] = CV_RGB(255, 239, 213); IplImage* img = cvCreateImage(cvSize(500,500), 8, 3); for (int Y=0; Y<img->height; Y++) { for (int X=0; X<img->width; X++) { float x = (X - img->width/2) / 200.0; float y = (Y - img->height/2) / 200.0; m_real = x;
m_image = y;
Complex a(x,y); float dist = Iteration(a, icount); CvScalar color = dye(dist); cvSet2D(img, Y, X, color); } } cvNamedWindow("Julia"); cvShowImage("Julia", img); cvWaitKey(0); //保存图片 char* path = "C:\\Users\\Administrator\\Desktop\\Julia.bmp"; cvSaveImage(path, img); cvReleaseImage(&img); }