分类模型评估——混淆矩阵、评估指标、ROC与AUC
混淆矩阵
混淆矩阵,可以用来评估模型分类的正确性。该矩阵是一个方阵,矩阵的数值用来表示分类器预测的结果,包括真正例(True Positive),假正例(False Positive),真负例(True Negative),假负例(False Negative)。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
#混淆矩阵
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import warnings
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 12
warnings.filterwarnings('ignore')
iris = load_iris()
x, y = iris.data, iris.target
x = x[y!=0, 2:]
y = y[y!=0]
y[y==1] = 0
y[y==2] = 1
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=2)
lr = LogisticRegression()
lr.fit(x_train, y_train)
y_hat = lr.predict(x_test)
#根据传入的真实值与预测值,创建混淆矩阵
matrix = confusion_matrix(y_true=y_test, y_pred=y_hat)
print(matrix)
#绘制视图
mat = plt.matshow(matrix, cmap=plt.cm.Blues, alpha=0.5)
label = ['负例','正例']
ax = plt.gca()
ax.set(xticks=np.arange(matrix.shape[1]),yticks=np.arange(matrix.shape[0]),
xticklabels=label, yticklabels=label, title='混淆矩阵可视化\n',
ylabel='真实值', xlabel='预测值')
for i in range(matrix.shape[1]):
for j in range(matrix.shape[0]):
plt.text(x=j, y=i, s=matrix[i,j], va='center', ha='center')
plt.show()
评估指标
对于分类模型,我们可以提取如下的评估指标:
- 正确率(accuracy)
- 精准率(precision)
- 召回率(recall)
- F1(调和平均值)
正确率
正确率定义如下:

精准率
精准率定义如下:
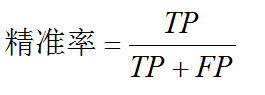
召回率
召回率定义如下:

调和平均值F1
调和平均值F1定义如下:

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print('正确率:', accuracy_score(y_test, y_hat))
#默认将1类视为正例,可以通过pos_label参数指定
print('精确率:', precision_score(y_test, y_hat))
print('召回率:', recall_score(y_test, y_hat))
print('F1调和平均值:', f1_score(y_test, y_hat))
print('score方法计算正确率:',lr.score(x_test, y_test))

ROC与AUC
ROC曲线
使用图形来描述二分类系统的性能表现,图形纵轴为真正例率(TPR),横轴为假正例率(FPR),其中真正例率与假正例率定义为:

ROC曲线通过真正例率与假正例率两项指标,可以用来评估分类模型的性能,真正例率与假正例率可以通过移动分类模型的阈值进行计算。随着阈值的改变,真正例率与假正例率也会随之发生改变,进而就可以在ROC曲线坐标上,形成多个点。
ROC曲线反映了FPR与TPR之间权衡的情况,TPR增长越快,曲线越往上凸,模型的分类性能就越好。
AUC
指ROC曲线下的面积,使用AUC值作为评价标准可以直观评价分类器的好坏,值越大越好。
ROC曲线程序示例
先看一个简单程序示例
import numpy as np
from sklearn.metrics import roc_curve, auc, roc_auc_score
y = np.array([0,0,1,1])
scores = np.array([0.2,0.4,0.35,0.8])
#返回ROC曲线相关值。返回FPR,TPR与阈值,当分值达到阈值时,将样本判定为正类,否则判定为负类。
#y_true:二分类的标签值(真实值)
#y_score:每个标签(数据)的分值或概率值。当该值达到阈值时,判定为正例,否则判定为负例。
#在实际模型评估时,该值往往通过决策函数(decision_function)或概率函数(predict_proba)获得
#pos_label:指定正例的标签值
fpr, tpr, thresholds = roc_curve(y, scores, pos_label=1)
print(f'fpr:{fpr}')
print(f'tpr:{tpr}')
print(f'thresholds:{thresholds}')
#auc与roc_auc_score函数都可以返回auc面积值,但是注意,两个函数的参数是不同的
print('AUC面积值:', auc(fpr, tpr))
print('AUC面积得分:', roc_auc_score(y_true=y, y_score=scores))

roc_curve函数的返回值
roc_curve函数具有3个返回值:
- fpr对应每个阈值(thresholds)下的fpr值
- tpr对应每个阈值(thresholds)下的tpr值
- thresholds函数
鸢尾花程序示例
#使用概率作为没有样本数据的分值
probo = lr.predict_proba(x_test)
fpr, tpr, thresholds = roc_curve(y_true=y_test, y_score=probo[:, 1], pos_label=1)
display(probo[:, 1])
#从probo[:, 1]中选择若干元素作为阈值,每个阈值下,都可以确定一个tpr与fpr
#每个tpr与fpr对应ROC曲线上的一个点,将这些点进行连接,就可以绘制ROC曲线
display(thresholds)
#随着阈值不断降低,fpr与tpr都在不断的增大
fpr, tpr
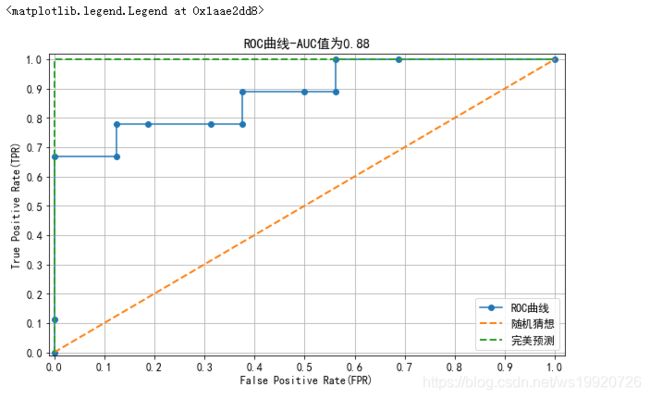
plt.figure(figsize=(10,6))
plt.plot(fpr, tpr, ls='-', marker='o', label='ROC曲线')
plt.plot([0,1], [0,1], lw=2, ls='--', label='随机猜想')
plt.plot([0,0,1], [0,1,1], lw=2, ls='--', label='完美预测')
plt.xlim(-0.01, 1.02)
plt.ylim(-0.01, 1.02)
plt.xticks(np.arange(0, 1.1, 0.1))
plt.yticks(np.arange(0, 1.1, 0.1))
plt.xlabel('False Positive Rate(FPR)')
plt.ylabel('True Positive Rate(TPR)')
plt.title(f'ROC曲线-AUC值为{auc(fpr, tpr):.2f}')
plt.grid()
plt.legend()