知识表示学习(七):TransGCN
一.摘要
链接预测是一项重要且经常研究的任务,有助于理解统计关系学习中知识图谱 (KG) 的结构。受图卷积网络 (GCN) 在图数据建模中的成功启发,我们提出了一个统一的 GCN 框架,名为 TransGCN,以解决此任务,其中同时学习关系和实体嵌入。为了处理 KG 中的异质关系,我们通过引入关于三元组的主体、关系和客体之间关系的变换假设,引入了一种表示异质邻域的新方法。具体来说,关系被视为将头部实体转换为尾部实体的转换运算符。在我们的框架中探索了 TransE 中的翻译假设和 RotatE 中的旋转假设。此外,TransGCN 框架不仅在基于卷积的编码器中学习实体嵌入,同时在解码器中学习关系嵌入,如 R-GCN 等最先进的模型,而是在训练过程中同时训练关系嵌入和实体嵌入。图卷积操作,因此与 R-GCN 相比具有更少的参数。
二.背景介绍
DBpedia 和 Freebase 等知识图谱 (KG) 对我们周围世界的陈述进行编码,越来越受到多个领域的关注,包括问答、知识推理、推荐系统等。就其本质而言,随着世界状况的不断发展,KG 还远未完成。 这激发了基于已知事实自动预测新事实的工作。在这些推理任务中,链接预测已成为统计关系学习 (SRL) 的主要焦点。
KG 将有关实体的结构信息和它们之间的丰富关系编码为有向标记的多重图,其中实体表示为节点,它们之间的关系表示为标记的有向边。在语义网上下文中,KG 中的语句可以表示为三元组 (h,r,t),其中 h 是头部实体,r 是关系,t 是尾部实体,KG 中三元组之间的连通性为链路预测提供了基础。
由于 KG 的符号表示禁止它们直接被纳入许多机器学习任务中,因此最近许多研究提出将 KG 的实体和关系嵌入到低维向量空间中,这可以在多个下游任务中进一步统一,例如, 上述链接预测。沿着这条线,有两个主要分支:1)基于翻译的方法,通过测量对应关系强制翻译后头部实体和尾部实体之间的距离来预测三元组的存在,例如 如 TransE、TransD 和 TransR和 2) 基于语义匹配能量的方法,它们测量三元组的存在作为两个实体的兼容性及其在潜在向量空间中的关系,例如 RESCAL,DistMult和ComplEx。最近,还有一些其他的想法将关系视为复杂向量空间中从主体到对象的旋转,并提出了 RotatE,这是第一个可以模拟处理对称/反对称、反转和合成关系的模型。
尽管在这两个分支中都有多个成功案例,但这些上述模型都独立地在单个三元组上进行了训练,而不管它们的本地邻域结构如何。 注意到这一不利因素,Schlichtkrull 等人指出,显式建模局部结构可以是帮助恢复 KG 中缺失语句的重要补充。 受图卷积网络 (GCN) 在使用卷积操作对未标记和无向图的结构化邻域信息建模方面取得成功的启发,作者提出了一种基于 GCN 的知识图建模方法 (R-GCN)。 在作为编码器的 R-GCN 中,每个实体的嵌入是基于其最多 n 度的相邻实体通过使用 n 个图卷积层来学习的。 然后编码器与特定于任务的解码器(例如,类似 DistMult 的解码器)一起训练,以预测链接。
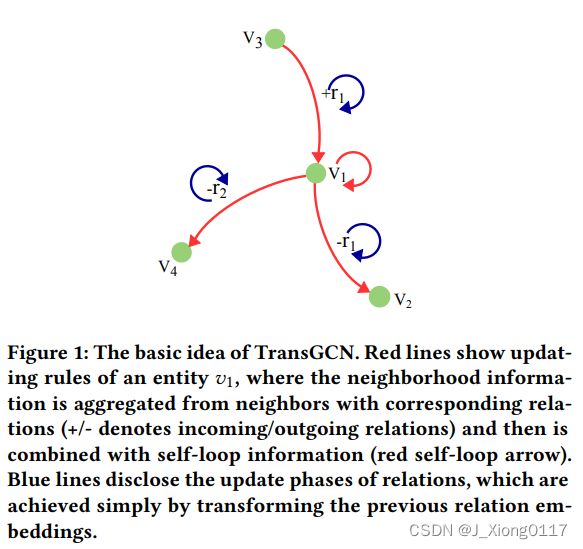
应用 R-GCN 的实验结果证明了在知识图嵌入模型中整合邻域信息的重要性。 R-GCN 旨在学习实体嵌入,即使它使用特定于关系的权重矩阵。 关系嵌入是在特定于任务的解码器中学习的,而在编码器中学习的特定于关系的矩阵被丢弃。因此,如果没有用于学习关系嵌入的特定任务解码器,R-GCN 无法直接支持链接预测等任务。 即使有额外的解码器可用,编码器-解码器框架也会遇到另一个问题,即在编码器端(特定于关系的权重矩阵)和解码器端(关系嵌入)中重复引入特定于关系的参数。 结果,参数的数量增加了。为了解决这个问题,我们提出了一种受 R-GCN 启发的新模型,这是一种基于 GCN 的知识图编码器框架,它可以通过执行从头部实体嵌入到尾部实体嵌入的特定关系转换来同时学习实体嵌入和关系嵌入 ,因此称为 TransGCN。原则上,任何假设的从主体到客体的转换假设,例如翻译假设、旋转假设等,都可以在所提出的框架中加以利用。以翻译假设为例,具体而言,通过关系作用的翻译算子被用来连接知识图谱中的实体。 TransGCN 的基本思想如图 1 所示。在这种情况下,TransGCN 首先将一个中心实体 vi 的 1 度邻居的嵌入与它们的特定关系嵌入进行转换。生成的嵌入用作中心实体 vi 的初始嵌入估计。然后对这些最初估计的嵌入执行卷积操作,为每个 vi 推导出一个新的嵌入 v′i,它对中心实体的局部结构信息进行编码。与 R-GCN 类似,将节点的聚合结构信息和自环信息结合起来进行实体嵌入更新。此外,我们还定义了一种新颖的关系嵌入卷积过程,以便可以像 GCN 一样以基于层的方式处理实体和关系嵌入。
三.TarnsGCN
R-GCN 模型不学习关系嵌入,因此在没有解码器的情况下不能直接用于链接预测。 此外,R-GCN 模型在编码器端和解码器端重复引入关系特定参数,导致参数数量增加。 我们认为,仅用于知识图谱应用的编码器应该同时编码实体和关系嵌入,以减少参数的数量(从而有助于缓解过拟合的问题),从而提高训练效率。
为了解决这些问题,我们提出了一个基于 GCN 的统一编码器框架来同时学习实体和关系嵌入,其中使用由关系执行的假定转换假设将 KG 中的异构邻域转换为同构邻域。 这随后被用于传统的 GCN 框架。 实体嵌入和关系嵌入都是以基于卷积层的方式学习的。 知识图 G = (V, E),其中 V 是节点/实体的集合,E 是标记边的集合,包含三元组 (vi,rk,vj) ∈ T 形式的语句,其中 vi、rk 和 vj 分别代表头部实体、关系和尾部实体。 在下文中,我们使用粗体文本来指代嵌入,我们将交替使用 (h,r,t) 和 (vi,rk,vj)。
1.处理 KG 中的异构邻域
传统的 GCN 在无标记无向图上运行,该图由相同类型的节点和相同类型的关系组成。 这意味着每条边具有相同的语义,并且节点的邻域是同质的,我们称之为同质邻域。 同质性使得聚合节点周围的本地邻域信息变得更加容易。 例如,在图 2(a) 所示的无向无标签学术合作网络中,简单地将来自 Wendy Hall、Dan Connolly、Ora Lassila 和 James A. Hendler 的信息汇总为传输给 Tim BernersLee 的消息是合理的,无需考虑消息的差异,因为它们在这样的图中的关系是相同的。
然而,在如图 2(b) 所示的知识图谱中,使用这种过于简化的求和是有问题的。 相邻实体通过不同方向的不同关系链接到中心实体。 例如,DeathCause 关系与 BirthPlace 关系非常不同,它们到 Vantile_Whitfield 的方向指向相反的方向,我们称之为异质邻域。 我们认为,为了使 KG 易于由基于 GCN 的框架处理,有必要将 KG 中的异质邻域转换为同质邻域。 在这项工作中,我们建议通过假设 KG 中的关系是将头部实体转换为尾部实体的转换操作来应对这一挑战。

两个实体之间常见的变换方式有平移(翻译)、旋转、反射等。 在任何这样的转换中,KG 中的一条语句都可以解释为头部实体通过关系转换为尾部实体。 更具体地说,语句中的尾部实体可以是经过平移/旋转后的头部实体。 因此,尾部实体的嵌入可以由头部实体在特定关系的转换操作之后进行估计。 为了便于概括,在变换假设之后的语句

关系类型的多样性和关系的方向性是异构图异质性的两个主要特征。 显然,在这个等式中,每种关系类型被不同编码的事实照顾了关系类型的多样性,并且转换算子通常专门设计用于处理关系方向。
基于翻译假设,我们定义从具有对应关系的连接实体派生的中心实体的估计作为实体邻居的嵌入。 以 TransE 为例。 给定一个具有输出三元组 (vi,rk,vj) 的实体 vi,我们将基于 (vi,rk,vj) 的 vi 估计 (vj−rk) 定义为 vi 的一个邻居的嵌入。 类似地,对于 vi 的传入三元组 (vl,rm,vi),另一个邻居的嵌入是 vl + rm,这是对中心实体 vi 的另一个估计。
形式上,在任何变换假设下,实体 vi 的嵌入估计可以如下所示:
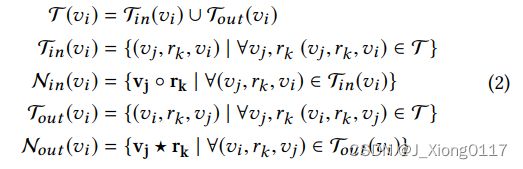
其中 T (vi) 表示与 vi 关联的所有三元组,包括作为传入三元组的 Tin(vi) 和作为传出三元组的 Tout (vi),Nin(vi) 和 Nout (vi) 都是导出的估计嵌入的集合 分别来自传入和传出的邻居。
在沿着不同的三元组路径进行这些转换操作之后,中心实体的最终估计嵌入应该与真正的中心实体具有相同的语义,由此将 KG 中的异质邻域转换为GCN可以轻松处理的同质邻域框架。
2.模型制定
我们的模型可以看作是 R-GCN 的扩展。 在下文中,我们将介绍我们的模型如何同时学习实体和关系嵌入。 与其他现有的 GCN 模型一样,我们的模型可以表述为消息传递神经网络 (MPNN) 的一个特例,它为图上的监督/半监督学习提供了一个通用框架。
一般来说,MPNN 定义了两个阶段:节点的消息传递阶段和整个图的读出阶段。由于在本文中我们关心节点和关系而不是整个图,因此我们只关注消息传递阶段。基本上,节点的这个消息传递阶段被执行 L 次以聚合多跳邻域信息,并且由消息传递函数 M(l) 和节点更新函数 U(l) 组成,其中 l 表示第 l 个隐藏层。 M(l) 主要聚合来自本地邻居的消息,而 U(l) 将 M(l) 与上一步中的自循环信息相结合。这两个函数都是可微分的。此外,吉尔默等人表明也可以通过为图中的所有边缘引入相似的函数来学习边缘特征,但到目前为止只有 Kearnes 等人已经实现了这个想法。为了适应我们的任务,我们为每个实体 vi 实例化 M(l) 和 U(l) 用于消息传播和实体嵌入更新,并另外引入关系的更新规则。

基本上,公式3中有两项用于对实体更新的局部结构信息进行编码,分别表示来自传入关系和传出关系的消息。 来自传入/传出关系的消息首先通过元素求和累加,然后通过线性变换传递。然后在下一步(公式 4)中,通过简单地将这些消息与自循环信息相结合以更新实体。 这个想法受到ResNet中的跳跃连接的启发,因此我们的模型至少可以像在该框架中实例化的基于转换的简单模型一样执行,图3说明了实体的计算图。 通常,公式3考虑实体的一阶邻居,可以简单地堆叠多个层以允许多跳邻居。此外,我们意识到等式中实体嵌入的每次更新(公式3和4)会改变原始向量空间。 因此,关系和实体之间的关系会受到影响,这使得在下一层它们之间无法执行假定的转换操作。 为了解决这个问题,而不是像公式3和4中那样为关系应用类似的消息传递机制,且为了提高效率,我们引入了一个变换矩阵 W(l)_1,对每一层的关系嵌入进行操作。我们假设引入的矩阵可以将关系嵌入投影到与新实体向量空间具有相同关系的向量空间中。 请注意,这是对向量空间的软限制; 也可以选择其他更严格的限制。 例如,对实体和关系的基向量进行约束,以确保这两个向量空间相同。 在软约束之后,各层关系的更新规则形成如下:

3.TransE-GCN模型
在翻译假设下,该关系被假定为从头实体到尾实体的翻译。 对于实体vi ,公式1可以实例化如下:

其中 ◦ 和 ⋆ 分别是 + 和 -。
就像在 TransE 中一样,三元组 (vi,rk,vj) 的得分函数根据以下定义:
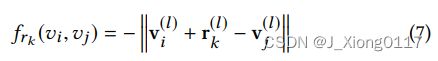
这个模型是用负采样训练的。 对于 KG 中的每个现有三元组,通过随机替换头部实体或尾部实体来构建一定数量的负样本(例如,一个正三元组和 10 个负样本)。 正样本预计得分高,而负样本预计得分低。 基于边际的排名函数被写为训练的损失函数:
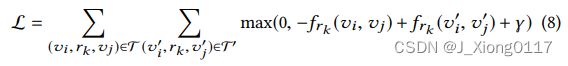
4.RotatE-GCN模型
最近在知识图嵌入中探索的另一个假设是旋转。 孙等人假设尾实体是在由复杂向量空间中的关系执行旋转后从头实体派生的。 因此,我们可以形式化实体 vi 的邻居:
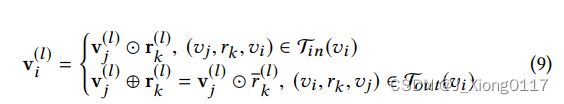
其中 ◦ 和 ⋆ 分别是 ⊙ 和 ⊕。 更具体地说,⊙ 是复空间中的元素乘积,r_k 是 rk 的复共轭。 | ri |= 1. 注意这里 rk 和 r_k 的存在而不是不同的变换算子保证了关系方向被自然地考虑。
类似地,距离函数用作评分函数:

为了与 RotatE 保持一致,我们采用自对抗负采样来训练模型,而不是普通的负采样。 自我对抗负采样的主要论点是,随着训练的继续,负三元组应该具有不同的抽取概率,例如 许多三元组可能显然是错误的,因此没有提供任何有意义的信息。 因此,根据当前的embedding模型,使用一个概率分布p来抽取负样本。
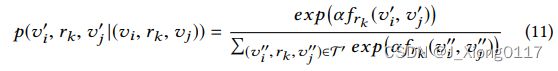
其中 α 是控制采样温度的常数,σ 是 sigmoid 函数。
然后将上述负样本的概率作为样本的权重来帮助构建损失函数。 对于一个正样本(vi,rk,vj),损失函数可以写成如下:

其中所有嵌入都在复向量空间中。
四.总结
在本文中,我们提出了一个统一的 GCN 框架 (TransGCN) 来同时学习关系和实体的嵌入。为了在使用传统 GCN 时处理知识图谱的异构特征,我们提出了一种将异构邻域转换为同构邻域的新方法通过引入转换假设,例如平移和旋转。在这些假设下,关系被视为将头部实体转换为尾部实体的转换算子。探索了平移和旋转假设,并将 TransE 和 RotatE 模型分别包装在 TransGCN 框架中。任何其他基于转换的方法都可以用作转换操作。通过这样做,具有关联关系的附近节点被聚合为像传统 GCN 那样传播到中心节点的消息,这有利于实体嵌入学习。此外,我们在同一个 GCN 框架中显式编码关系,以便关系嵌入可以同时与实体无缝编码。从这个意义上说,我们的 TransGCN 框架可以被解释为一种新的(知识)图编码器,它同时产生实体嵌入和关系嵌入。该编码器可以进一步合并到任何其他任务的编码器-解码器框架中。在两个数据集 FB15K237 和 WN18RR 上的实验结果表明,我们的统一 TransGCN 模型,TransE-GCN 和 RotatE-GCN 模型在所有指标方面始终优于基线 R-GCN 模型,这证明了处理异构邻域的转换思想的有效性。此外,这两个模型的性能都优于它们的基础模型,即 TransE 和 RotatE,显示了在知识图嵌入学习中显式建模局部结构信息的重要性。在本文中,尽管在我们的 GCN 框架中对关系进行了编码和学习,但它们只是通过单独的线性变换进行更新。未来,我们计划探索直接对关系进行卷积操作的方法,以便图的局部结构也可以在关系嵌入学习中发挥作用。此外,应该研究一种加权机制来衡量邻居的不平等贡献。
