用相关函数法计算信号的延迟量
在信号处理领域中,我们经常会用到自相关函数和互相关函数,例如利用自相关函数在语音信号处理中提取基音频率,又例如常利用互相关函数提取两接收信号之间的时间延迟。一般是用线性相关函数,但用FFT方法可快速计算线性相关和循环相关。循环相关比线性相关的计算量更小,那么是否能用循环相关获取延迟量呢?在某些情况下是可以使用的!
当相关函数的峰值结构衰减很快时,可以从循环相关中提取峰值,从而得到延迟量。
当相关函数的峰值结构衰减很慢时,就不能从循环相关中提取峰值了,从而得到延迟量。
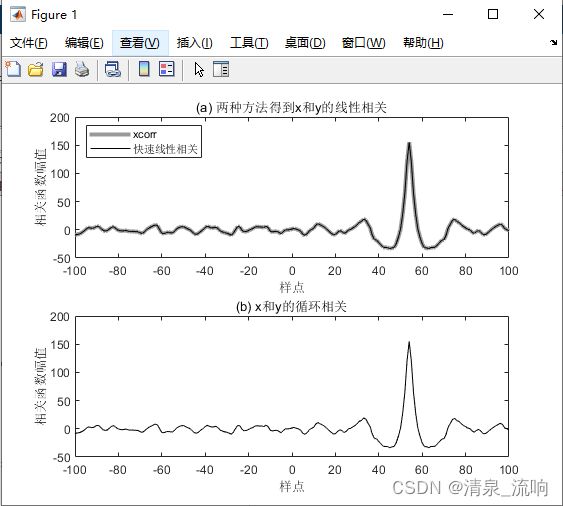
案例1、从delaydatal.txt文件读入两通道数据,分别设为x和y。它们之间的延迟量为54个样点,以xcorr、快速线性相关和循环相关计算延迟量,比较它们的结果,程序如下:
clear all; clc; close all;
xx=load('delaydata1.txt');% 读入数据
x=xx(:,1); % 设为x
y=xx(:,2); % 设为y
N=length(x); % 数据长度
[Rxy,lags]=xcorr(y,x); % 用xcorr计算线性相关
% 快速计算线性相关
X=fft(x,2*N); % FFT
Y=fft(y,2*N); % FFT
Sxy=Y.*conj(X);
sxy=ifftshift(ifft(Sxy));% IFFT,调整序列排列
Cxy=sxy(2:end); % 只取2*N-1点
% 作图
subplot 211;
line([lags],[Rxy],'color',[.6 .6 .6],'linewidth',3); hold on
plot(lags,Cxy,'k'); axis([-100 100 -50 200]);
box on; title('(a) 两种方法得到x和y的线性相关')
xlabel('样点'); ylabel('相关函数幅值')
legend('xcorr','快速线性相关','Location','northwest')
% 计算循环相关
Xc=fft(x); % FFT
Yc=fft(y); % FFT
Scxy=Yc.*conj(Xc);
scxy=ifftshift(ifft(Scxy));% IFFT,调整序列排列
Ccxy=scxy(2:end); % 只取N-1点
lagc=-N/2+1:N/2-1; % 设置延迟序列
% 作图
subplot 212; plot(lagc,Ccxy,'k');
axis([-100 100 -50 200]); title('(b) x和y的循环相关')
xlabel('样点'); ylabel('相关函数幅值')
set(gcf,'color','w')运行结果如下:
在本程序中用两种方法计算线性相关:用xcorr函数和FFT得到上图,可以看出这两种方法得到的相关函数很好地重叠在一起,且计算出延迟量为54个样点。而通过FFT计算得的循环相关函数,也可以看出也能很好地反映出延迟量为54个样点。
delaydatal.txt文件的数据是振动信号,周期性不强,所以可以用循环相关法提取延迟量。
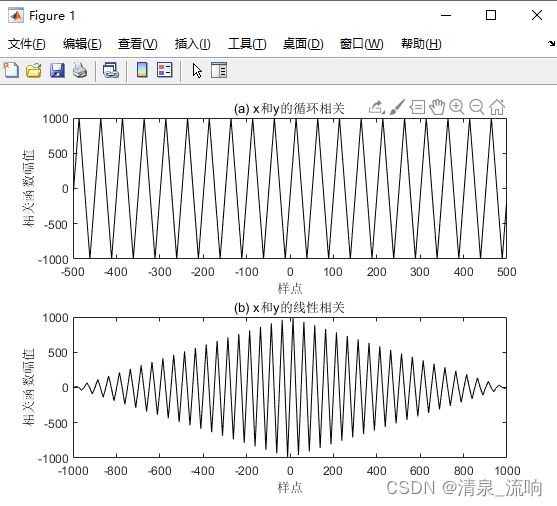
案例2、从delaydata3.txt文件读入两通道数据,分别设为x和y。它们是矩形脉冲,两序列之间的延迟量为14个样点,以xcorr线性相关和循环相关计算延迟量,并比较它们的结果。程序如下:
clear all; clc; close all;
xx=load('delaydata3.txt');% 读入数据
x=xx(:,1); % 设为x
y=xx(:,2); % 设为y
N=length(x); % 数据长度
fs=1000; % 采样频率
Xc=fft(x); % FFT
Yc=fft(y); % FFT
Scxy=Yc.*conj(Xc); % 计算循环相关
scxy=ifftshift(ifft(Scxy));
Ccxy=scxy(2:end); % 循环相关函数
lagc=-N/2+1:N/2-1; % 延迟量刻度
% 作图
subplot 211; plot(lagc,Ccxy,'k');
title('(a) x和y的循环相关');
xlabel('样点'); ylabel('相关函数幅值')
[Rxy,lags]=xcorr(y,x); % 计算线性相关
%[maxr,locr]=max(Rxy);
% locr=locr-1000;
% 作图
subplot 212; plot(lags,Rxy,'k');
title('(b) x和y的线性相关')
xlabel('样点'); ylabel('相关函数幅值')
set(gcf,'color','w')运行结果如下:
从图中可看到y对x有14个样点的延迟量。用循环相关法计算得到的相关系数中有几个数值相同的峰值,不可能找最大峰值来获取延迟量;而通过线性相关仍可以观察到它们之间的延迟关系,进一步计算的话能提取到延迟量为14个样点。
通过上面2个案例得出结论:当信号是周期性的时,就不能从循环相关函数中获取延迟量,这也说明了要从循环相关函数中获取延迟量是有条件的。
实验数据下载链接如下:
https://mp.csdn.net/mp_download/manage/download/UpDetailed
https://download.csdn.net/download/qq_42233059/86406504
参考文献:MATLAB数字信号处理85个实用案例精讲——入门到进阶;宋知用(编著)